Perimeter and Area
We will now take a look at the perimeter and area of 2 sided shapes. Perimeter is quite easy to calculate, with the possible exception of the perimeter of circle which is correctly called the circumference and is subject of a formula rather than a simple addition (see the section that concerns circles for more information).
We define “the perimeter” as “the distance all around” the shaped concerned.
The perimeter of any N sided shape is calculated simply by adding up the length of the N sides, whether the shape is “regular” or “irregular” so for example the perimeter of the below triangle is evaluated quite simply by adding up the length of the sides.
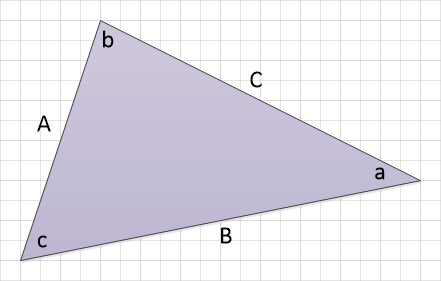
- Let A = 12
- Let B = 20
- Let C = 14
From this it is quite simple to say that the perimeter is 12+20+14= 46 of whatever unit you choose.
If the shape is irregular you have to add up the sides, this can of course become laborious if you have many sides, but on the other hand if the shape is regular (that is all of the sides have the same length) it is simpler to just multiply the number of sides by the length of one of them:
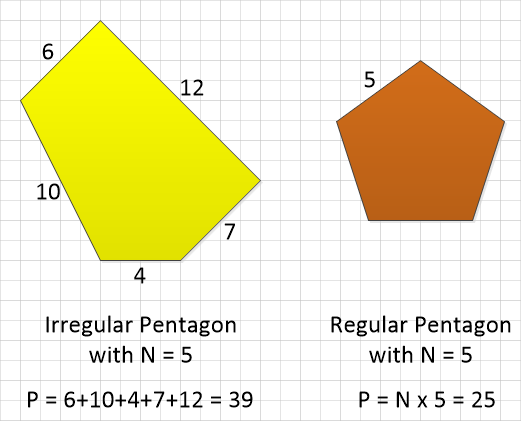
Please note that in the picture above, the shapes are not drawn to any particular scale. They have a grid behind them but that is just something that the software I used to create them gives me.
There isn’t really much more to say about perimeters, so now we will move onto areas.
Area of a Triangle
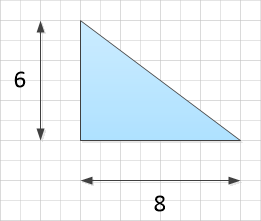
The area of the triangle is given by the equation:
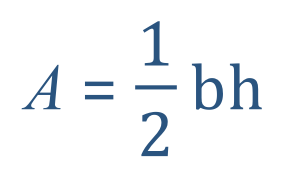
Where ‘b’ is the base length and ‘h’ is the perpendicular height. In this particular example I have deliberately chosen a right triangle because the side marked ‘6’ is in fact also the perpendicular height.
The area of this triangle is 24 square units.
Things aren’t quite as straightforward when we start looking at less regular triangles, for example equilateral, isosceles and of course scalene triangles.
It may be that you are given the perpendicular height even though the triangle may not be regular:
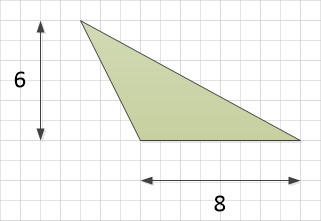
Although these 2 triangles look remarkably different, they do share one thing in common, they have the same area. This is because the base is 8 in both cases and the perpendicular height is also the same in both cases, being 6.
Therefore using the formula we can conclude that the area of this triangle is also 24 square units. It may be that you’re given a slightly less strange looking triangle:
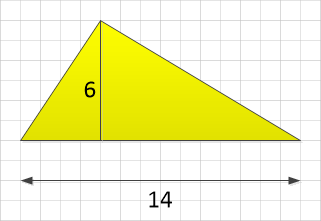
This one is quite simple, half of the base is 7 and the perpendicular height is 6 as shown therefore the area is 42 square units.
If you had access to other information, such as for example other side lengths you could be asked to evaluate the areas of the 2 triangles shown and then add them together, but this would depend on the number of marks being allocated to the question.
If the examiner is being particularly nasty, (s) he could give you this:
“Calculate the area of the triangle ABC”
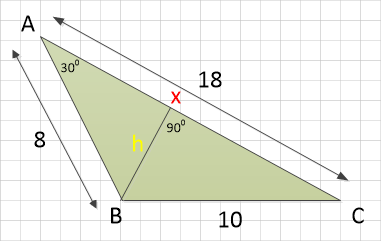
Now then, where do we start with this one?
Although this is a bit of a combination of trigonometry and two-dimensional geometry it’s still distinctly possible that it could come up on an examination paper somewhere:
Step 1 - we are given the angle 30° and we can see from the diagram that the line connecting point B to the point marked ‘x’ on the longest side is going to be the perpendicular height of the triangle if we flip it over onto its longest side (side AC).
Step 2 - the perpendicular height of the triangle is given by the formula:
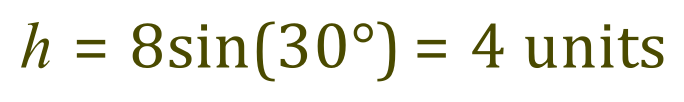
Depending on whether or not you’ve covered the trigonometry section of this book already, you may need to stop and study this expression to try to work out where I got it from, if not I want you to simply accept (for the time being anyway) that the triangle containing the 30° angle at point ‘A’ (that is the triangle ABx) is a right angled triangle (at point x) and therefore we can use SOHCAHTOA:
Step 3 - Using SOH:
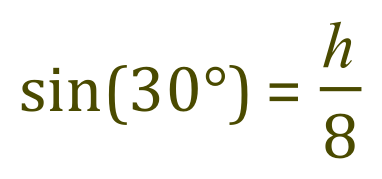
From this we can work out that ‘h’ is 8 sin (30) which is 8 × 0.5 = 4.
We now have the perpendicular height of our triangle, and we can now see that using the standard triangular formula given previously many times, the area of the triangle ABC is 36 square units:
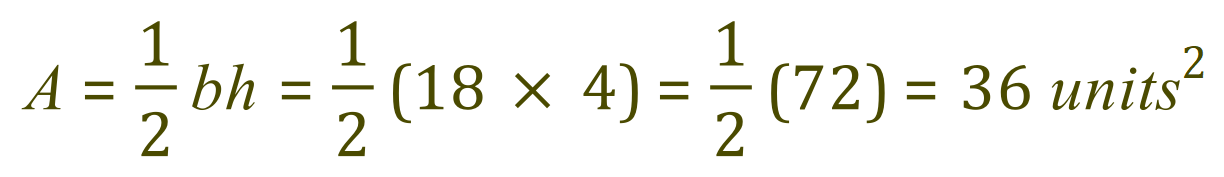
Although the previous example was quite tricky, it is likely that you will (especially in examination conditions) be given the perpendicular height and simply asked to evaluate the area for, perhaps 1 or 2 marks.
How could you work out the area of the following triangle?
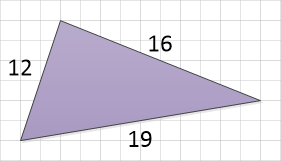
Well, you could work out individually the values of 2 of the angles using the cosine rule and then by the rules of the sum of the internal angles of a triangle deduced the 3rd but this may not particularly help you when you try to establish the perpendicular height. There is a simpler way involving the perimeter and a little bit of basic arithmetic, attributed to the Greek engineer and mathematician Heron (or Hero) of Alexandria around about 70 A.D.
Heron’s method is a two-stage process:
Step 1 - calculate the perimeter and divide it by 2, attribute this result to the variable ‘s’
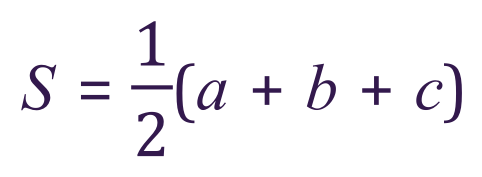
Step 2 - substitute your new found value for ‘s’ and sides ‘a’, ‘b’ and ‘c’ into the following equation:
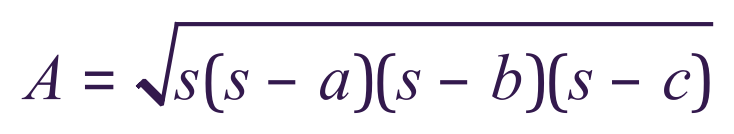
Let’s see if this works by comparing it to the easily calculable area of a right angled triangle as it is a formula which is supposed to work for any triangle.
Take the following right angled triangle below:
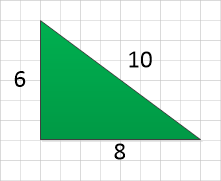
Just for the sake of simplicity I have chosen example of a “345” triangle, Pythagoras theorem tells us that the hypotenuse is 10 because the square root of 6 squared + 8 squared is 10.
Now we shall see if Heron’s formula does in fact work.
Step 1 - the perimeter of this particular triangle is 24 therefore the value for our variable ‘s’ will be 12
Step 2 - substituting into the second stage equation for the area:
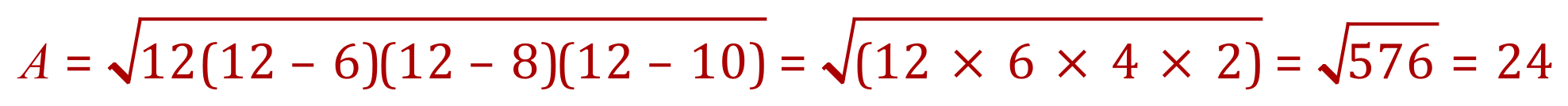
According to Heron’s formula then this particular triangle should have an area of 24 unit squared. We can see that the perpendicular height of the triangle is 6 and that the base is 8 so using the standard formula for the area of a triangle:
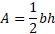
We can substitute values for ‘b’ which is the base and ‘h’ which is the height:
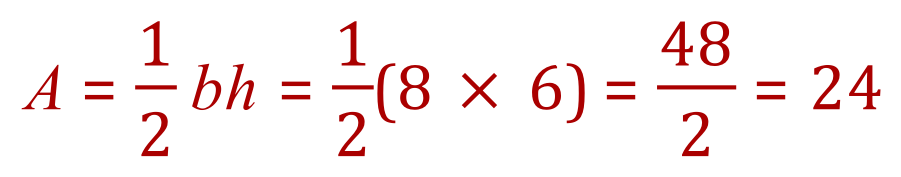
This result has in fact borne out Heron’s formula by producing the same result of 24 square units.
Let’s have a look at a more complicated example:
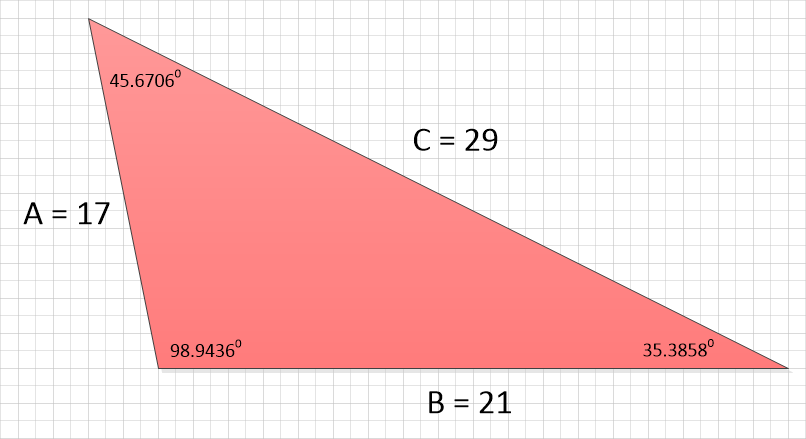
Quite a bit more complicated than previous examples we’ve come across, and we have no obvious way of working out (at this stage anyway) the perpendicular height so there isn’t a particularly simple way (using the perpendicular height that is) to evaluate the area of this particular triangle.
Let’s see what Heron’s formula can offer us:
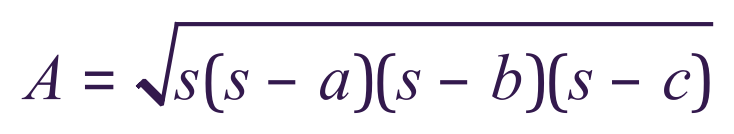
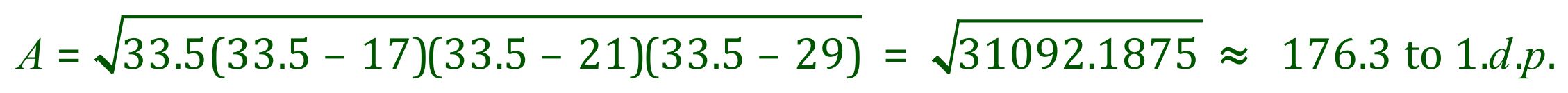
Okay so Heron’s formula gives us an answer, but how do we know it’s right? Well, let me now introduce you to another way of calculating the area of a triangle where we know 2 sides and the angle between them. In fact in this particular triangle we know all 3 sides and all 3 angles so we have 3 ways of doing this, but we will satisfy ourselves with just one for now.
Given side A and side B and the value of the angle between them, the area of a triangle is given as:
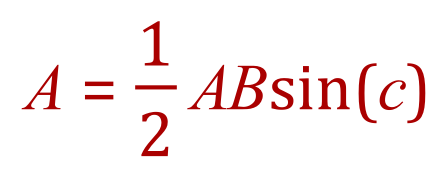
Where ‘c’ is the angle between the lines A and B, facing the unknown / unused side C. If we take a look at our triangle above we can see that A equals 17 units and B equals 21 units, the angle between them (angle c) is 98.9436°
Using our newly introduced formula above:
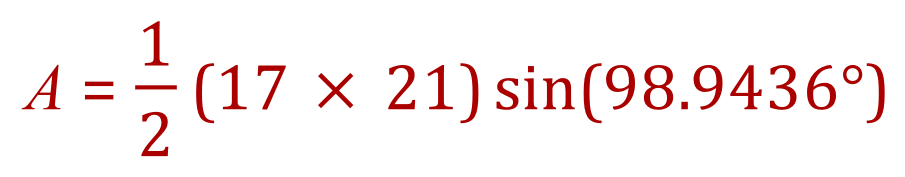

What a pleasant surprise? This result bears out Heron’s formula exactly!
There are two other permutations to the new equation:
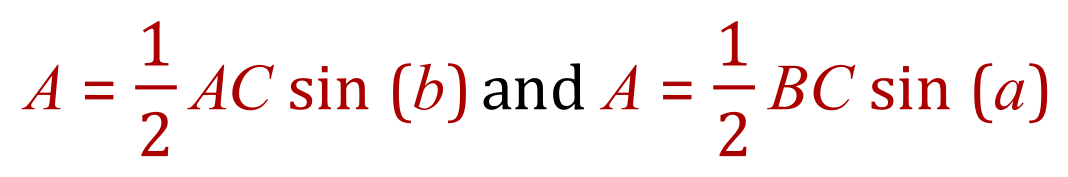
These permutations are used of course when you have A and C or B and C and the corresponding angle between the two.
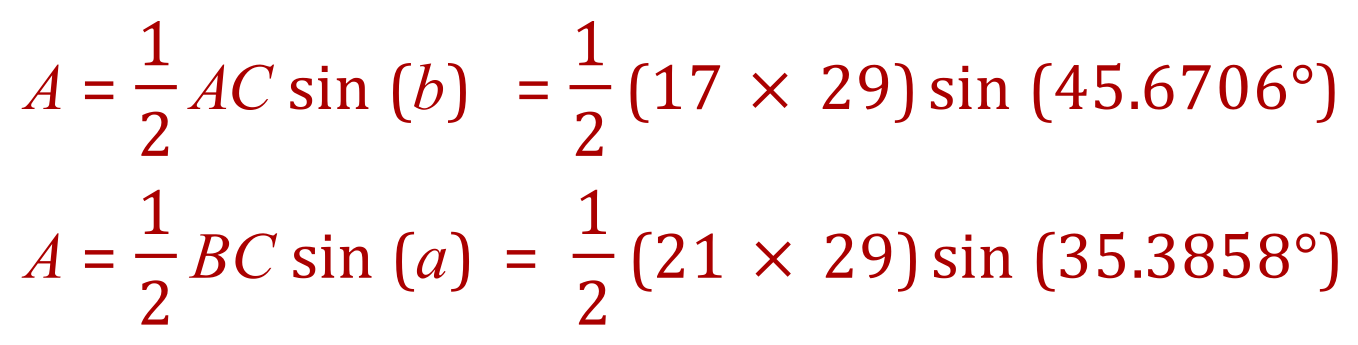
If you evaluate these, you will find that the answer is the same as before, 176.3 units to 1 decimal place. I’m sure you’ll agree that this is quite fascinating stuff eh?. OK we should now move on to the next of our two-dimensional shapes, the square.
The Square
The square is perhaps one of the most ubiquitous shapes you are going to come across.
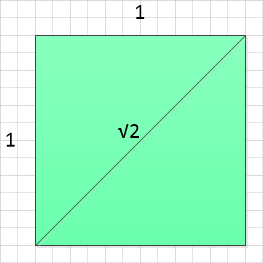
From Pythagoras theorem we can evaluate quite simply that the length of the diagonal, as shown is “root 2” or approximately 1.414. It can be shown quite simply that for a square of side length “N” the diagonal will be “root 2” times N:
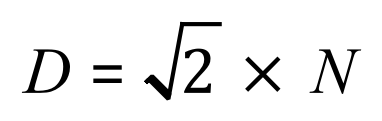
And this can be used as a very quick way to roughly estimate the length of the diagonal of any known square, for example if you know that your square as a side length of 4 then the diagonal is approximately 5.6 (1.4 x 4).
It is very easy to calculate the area of square, by virtue of the very name of the object we simply take the value of the side and square it:
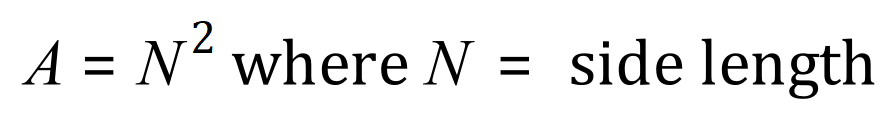
But there is another, less obvious way of working out the area of the square which is to square the length of the diagonal (should you know this) and then divide the result by 2:
Using the example above:
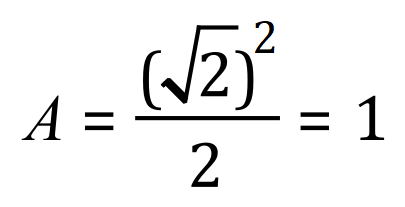
This is probably little bit of “stating the obvious”, so let’s go for a slightly more complicated example:
Let the side of a square be 17 units in length, we know that the area will be therefore 289 square units as this is the result of 17 squared.
Our diagonal will be “17 root 2”:
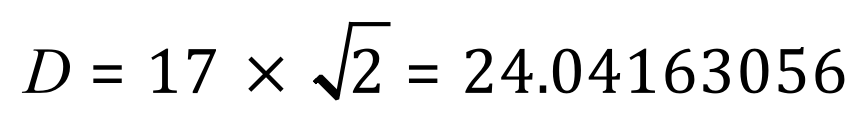
Notice that I’m deliberately working to full calculator accuracy because I don’t want much error in the result I’m trying to prove.
Using the formula:
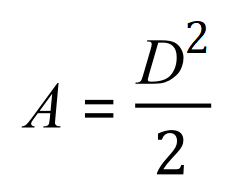
Where of course D is the diagonal length and A is the area:
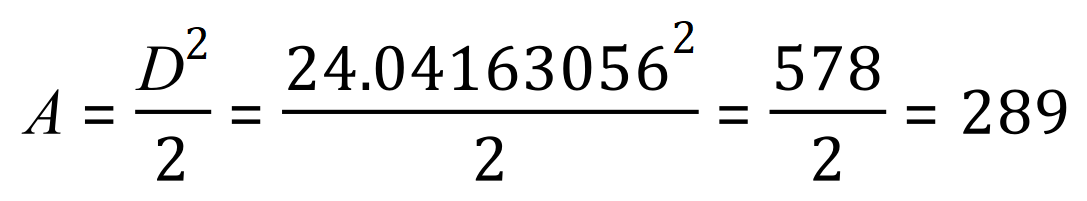
A useful formula, although you will probably never use it as squaring the side length is far simpler.
We are about to move onto N Gons which have 5 or more sides. Instead of explaining these somewhat more complicated shapes here, I have continued this particular argument in two further chapters of the book:
“Areas Of N Sided Polygons” and “Volumes of Solid Shapes”.
You should refer to these sections for further discussion. There is a little overlap between the sections but you should consider this as “revision” 8-)