Worked Examples in Science and Mathematics

So what do we mean by "exchange surfaces"? Well living things depend on gases and other dissolved substances in order to survive. These gases/dissolved substances need to get into the body somehow, and any waste products need to get out of the body. It is diffusion through the walls of the cells which enable this to happen and the surface of the cell is where the exchange has to take place, hence the expression exchange surfaces.

When we breathe, for example we take in oxygen and we expel carbon dioxide. These gases have to be transferred between cells in order to be brought in from the environment (oxygen) and released back to the environment (carbon dioxide). The amount of dissolved gas that a particular cell needs relies on how quickly it can be drawn through the cell membrane, the diffusion of these gases/substances across the exchange surface needs to be quick enough to satisfy the needs of the cell.

In the case of, say for example a single celled organism, the actual volume of the organism and the surface area of the cell membrane are reasonably well matched, in other words the surface area compared to the volume of the organism is large enough for the needs of the organism to be satisfied by simple diffusion through the cell membrane, but in a multicellular organism this system may not be efficient enough as the total volume of all the cells and the total surface area available may not be matched very well, in other words the surface area may not be sufficiently large to make sure that the cells receive all of the nourishment that they need. In these cases an alternative mechanism needs to be used.

The "surface area" to "volume" ratio is very important, and the closer these are together, the better. If an organism has a large surface area and a relatively small volume by comparison, such as in the case of an earthworm, which exchanges gases through its skin, then this sort of transport is quite sufficient to make sure that all of the cells receive sufficient quantities of gases and dissolved substances that they will need.

Organisms with large numbers of cells, for example humans where there are trillions of cells, need to develop quite specialised gas exchange mechanisms where the surface area is as large as it can possibly be. The larger the surface area, the more gas can be exchanged in unit time.

In the human lung, the alveoli are where the gas exchange takes place. There are literally millions of these little air sacs in our lungs, each of which is capable of accepting oxygen through it and passing carbon dioxide back through it into the blood. The capillaries which surround the alveoli are responsible for delivering, dioxide back to the lungs to be dispersed into the atmosphere and for accepting oxygen into the circulatory system to be passed to the cells that need it. This type of diffusion is from areas of the high concentration, to areas of low concentration as you would expect.

• When we breathe in, there is a higher concentration of oxygen inside the alveoli than there is in the capillary blood, therefore the diffusion goes from a higher concentration to a lower concentration, i.e. oxygen diffuses across the membrane and into the blood.
  
  
• When we breathe out there is a high concentration of carbon dioxide in the capillary blood, higher than that inside the alveoli therefore carbon dioxide passes from an area of high concentration to an area of low concentration and is expelled from the lungs.

Why are there so many alveoli?

The greater the number of alveoli, the greater the overall surface area and the more efficient the diffusion of oxygen and carbon dioxide gases to and from the bloodstream. Organisms which do not have such complicated needs, such as worms are able to breathe through their skin, by simple gas exchange through the skin. However larger animals such as elephants, hippopotamuses, humans et cetera have more complex needs and so gas exchange systems utilising lungs (a more efficient diffusion system) is required.

How can we visualise the surface area?

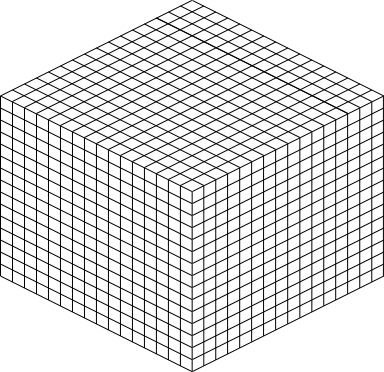
Well, it's time to do some mathematics to show this. Let's consider for the sake of simplicity a cube of side 4 cm:

Go To >> Nanoparticles <<

>> Questions <<