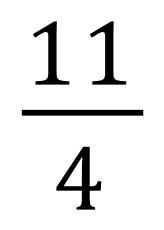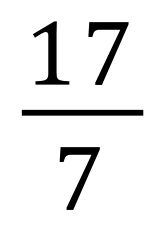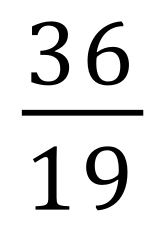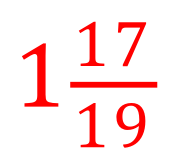Fraction Arithmetic
What is a Fraction? Well it is a “part of something”, so if for example we buy a cake or a pizza and eat only some of it, we have “eaten a fraction” of the cake or pizza. Just how big the fraction is depends on what’s been eaten and what’s left.
Fraction - “A fraction is PART of a WHOLE”
There are many different types of fraction, but before we look at these, let’s look at the THREE components that make a typical fraction:
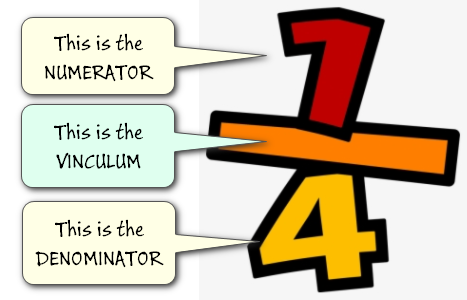
The Vinculum is usually just called “The Fraction Bar”.
Generally, the numerator is bigger than the denominator, because a fraction is usually part of the whole, not equal to it or more than it. Having said that sometimes the numerator can be bigger than the denominator, this doesn’t seem right so it is referred to as an improper fraction, whereas the fraction that we are used to is called a proper fraction. Let’s take a look at these other fraction types now:
Proper Fractions and Improper Fractions

As you can see a proper fraction is when the number at the top is smaller than the number at the bottom. If we turn each of the numbers above upside-down, so we have “4÷3”, “3÷2” and so on right up to “2÷1” these would become improper fractions.
Mixed Fractions / Mixed Numbers
It isn’t usually the case that we leave a fraction in its improper form, although sometimes it helps to work that way until the very end of the question when we would normally turn the fraction into a mixed fractions/mixed number. A mixed number is the number of wholes that we can make out of a fraction, showing what’s left as a proper fraction the side:
Let us take for example, the improper fraction “20÷3” :
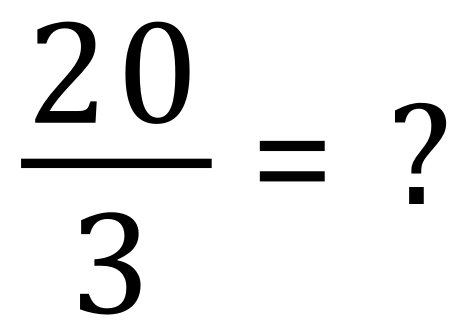
To make this into a mixed number we need to work out how many “wholes” are in it, that is how many times does 3 (the denominator) go into 20 (the numerator)?
From your multiplication tables you should be able to tell me that 3 goes into 20 a total of 6 times but we have a “2” left:

We can check that this is right, by multiplying the red 3 (denominator) by the black 6 (the number of complete “wholes”) and then add on the blue 2, this will make 20 which is what we started with.
Exercises:
Convert these improper fractions into mixed numbers:
|
|
|
|
|
|
|
|
|
|
|
|