Reciprocals
The reciprocal of the number is probably best thought of as "one over the number". So for example if we look at the number three, the reciprocal is one over three, or one third.

There is arguably an even simpler way to look at "reciprocals", and that is to just completely flip the number on its head. we will come to this soon. The "one over the number" method works fine when you are talking about integers, that is whole numbers, but can start to get a little bit confusing when you're talking about fractions, for example what would be the reciprocal of three quarters?
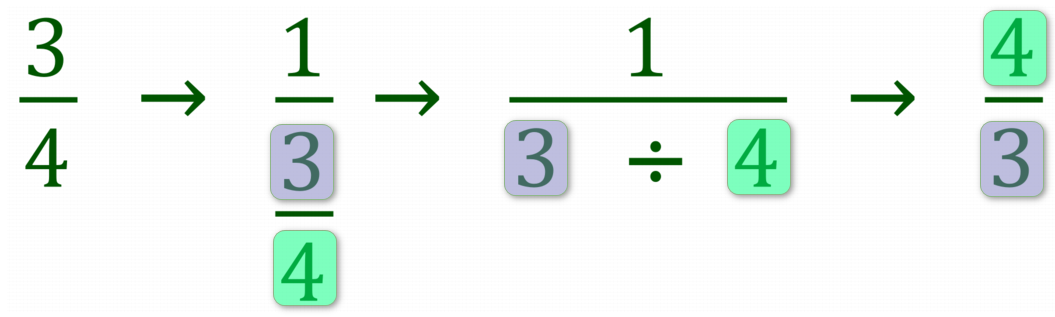
As you can see, this can get a little bit messy. The reciprocal of three quarters is in fact four thirds but by representing it as it is in the diagram above, matters have been unnecessarily complicated. The simplest thing to do is to just take the number and flip it on its head, so "3÷4" has the reciprocal of "4÷3".
The mathematical definition of a reciprocal is its "multiplicative inverse", which is the number that we need to multiply by to get 1. Let's take a look at our example above, applying this definition and you will see that it is in fact spot-on:
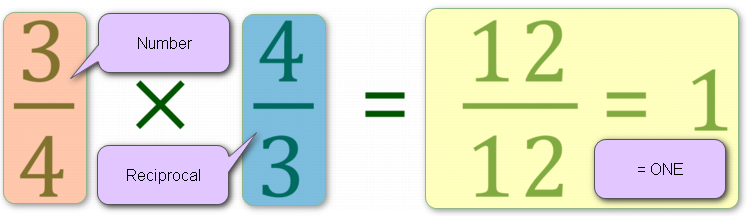
MULTIPLICATIVE INVERSE = "A NUMBER MULTIPLIED BY ITS RECIPROCAL IS ALWAYS EQUAL TO 1"
You will find this "multiplicative inverse" very useful when you start to look at (that is, assuming that you haven't already) fractions, and the multiplication and division of them with each other.