This question also appeared in the news around August 2023 as it was given as homework to a student somewhere in the UK whose parents brought it to the attention of the media. It is allegedly aimed at 10 year olds in Year 6. See what YOU think:



There are a couple of ways to approach this question. My choice would be an algebraic solution but there is a solution available using geometry and pie charts. I will look at this one first.


Start from the end and work forwards. We are told that Hasim has HALF of his money left at the end, SO the THIRD goiven to his brother and the £12 spent on his sister must account for the other half. This is best visualised as a pie chart:



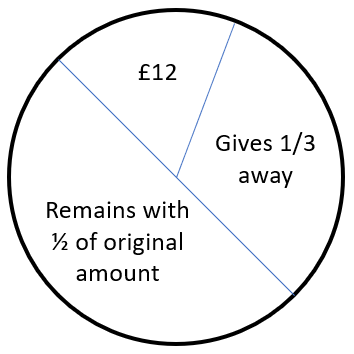
Now let us look at changing the fractions mentioned into a common denominator:


1. Hasim gives 1/3 of his money away to his brother, we can alternatively call this 2/6

2. Hasim remains with 1/2 of his money, we can alternatively call this 3/6

3. The remaining 1/6 in this new depiction is the £12 that the gift cost.


Looking at this, if 1/6 of the total is £12, then by a sneaky peek into algebra:



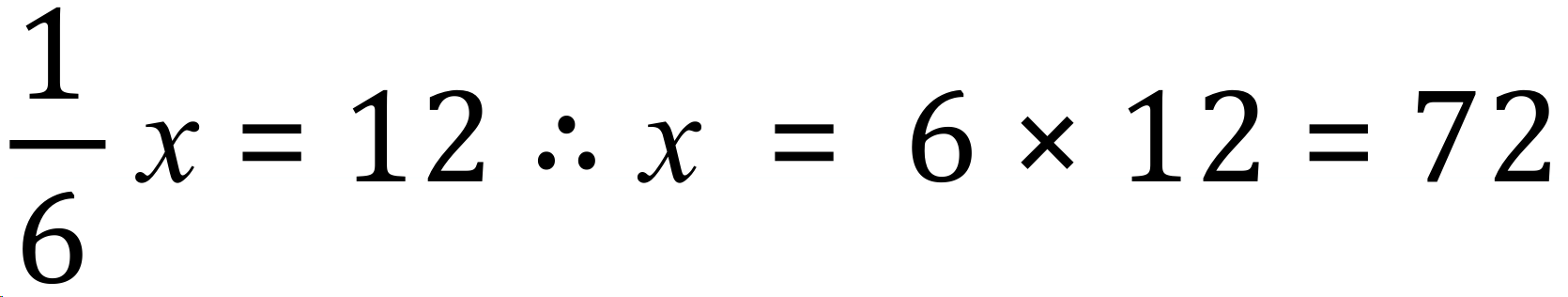
Hasim gives 1/3 of the total "x" to his brother, this is the required answer to the problem:




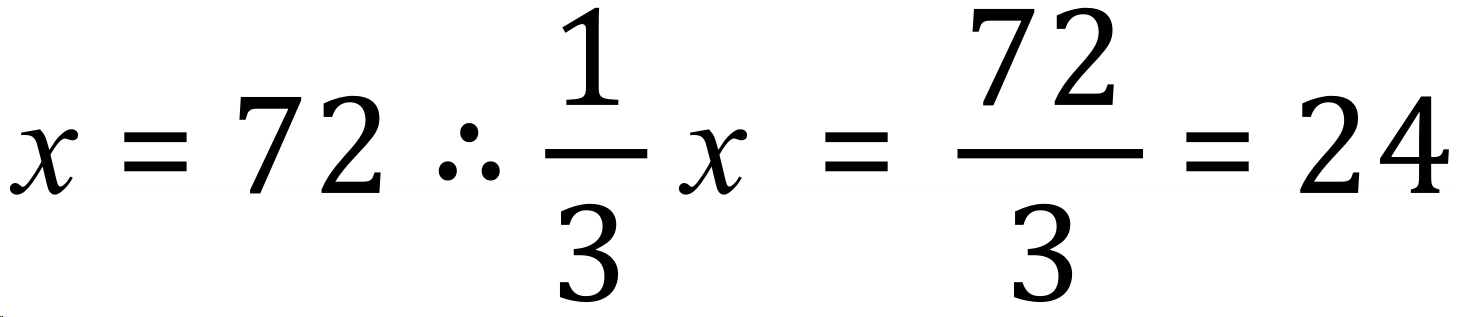
The fully algebraic response would be something like this:


1. Let the total amound that Hasim had to start with be "x"

2. Hasim gives away 1/3 x to his brother

3. Hasim spends £12 on his sister.

4. Hasim ends up with 1/2 of the original amount.


So ..... the totals of 1, 2 and 3 MUST equal 4. As an expression / equation this would be:



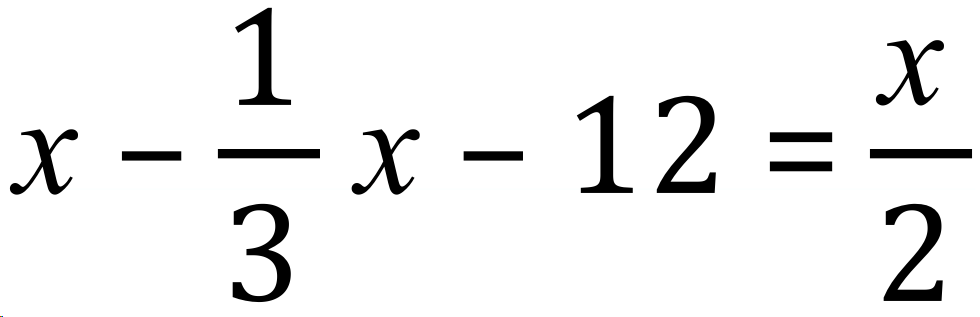
The crux of this question is to now rearrange the equation in terms of "x" and solve for "x".


Step 1 - Multiply BOTH sides by 3 to remove the first fraction:



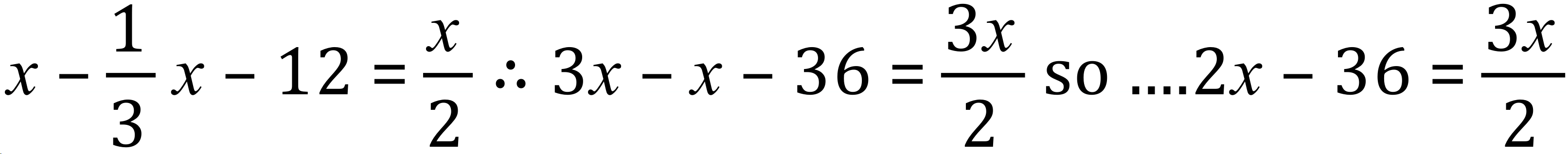
Step 2 - Always useful to eliminate ALL fractions so once again we multiply, this time by 2:




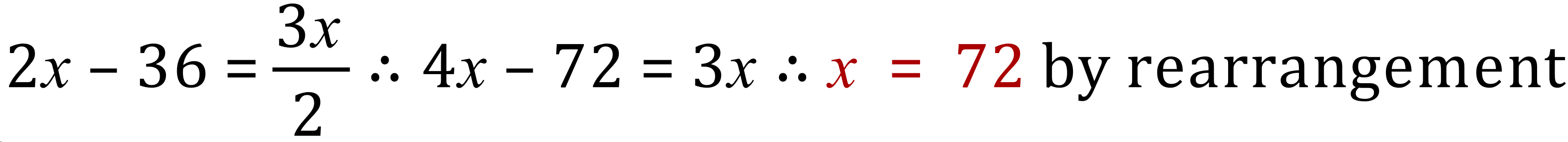
Finally we answer the question, having established that Hasim had £72 at the start he gives 1/3 of 72 to his brother = £24.