Graphing Quadratic Functions
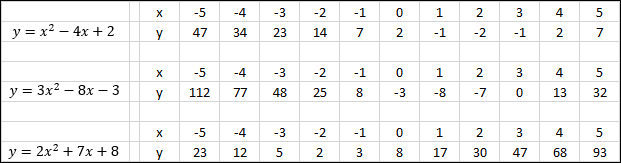
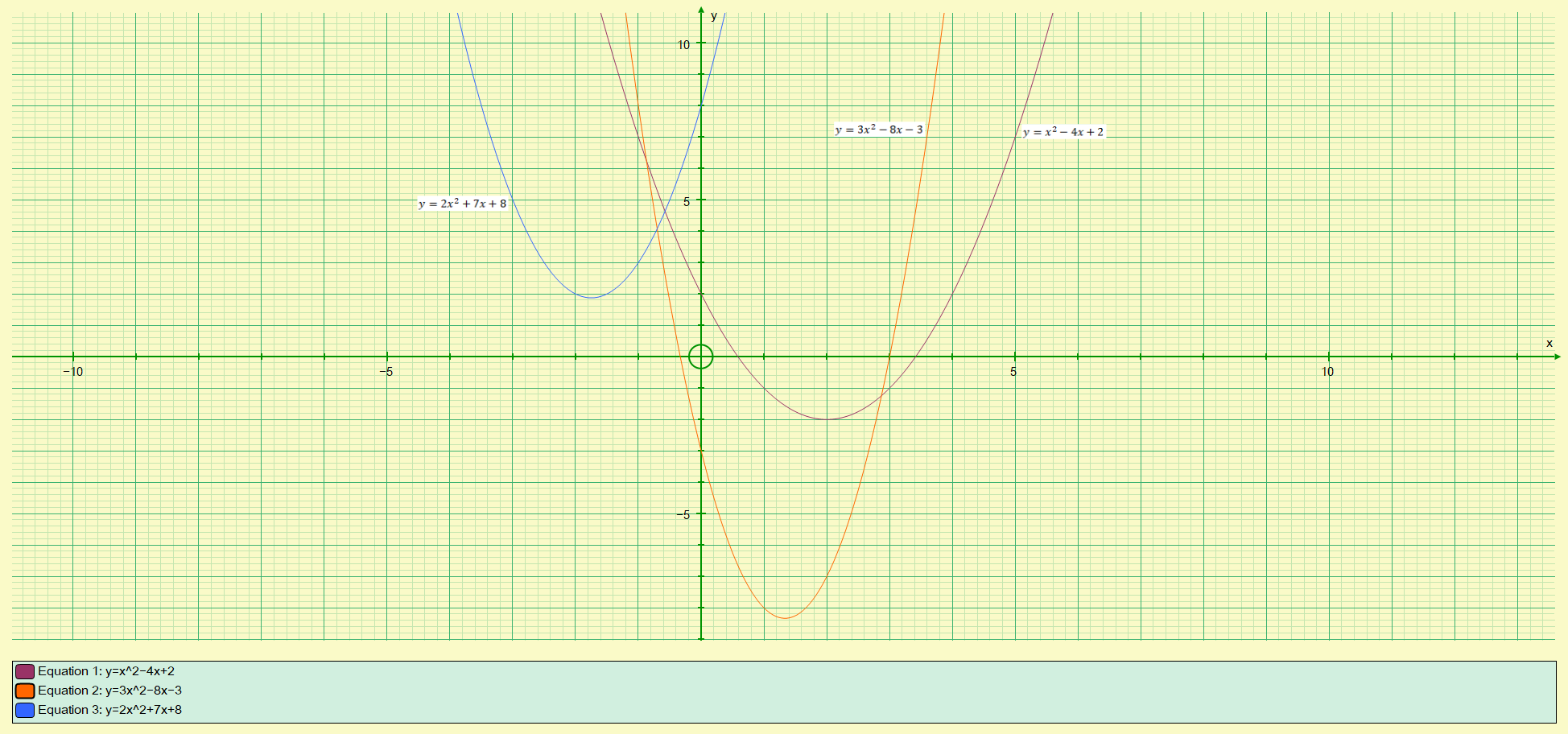
Q1. Complete the table of values for the given Quadratic Function and plot the curve against appropriate axis values:
(a)
(b) Using the Quadratic Formula, for each equation in the table above, evaluate the values of 'x' that satisfy the equations, ie: work out the roots of each quadratic.
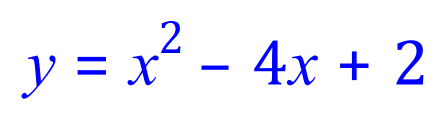
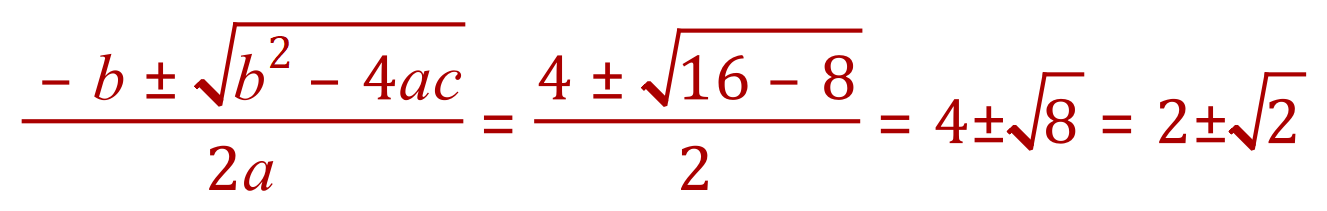
Numerically the roots approximate to 3.414 and 0.586 to 3 d.p.

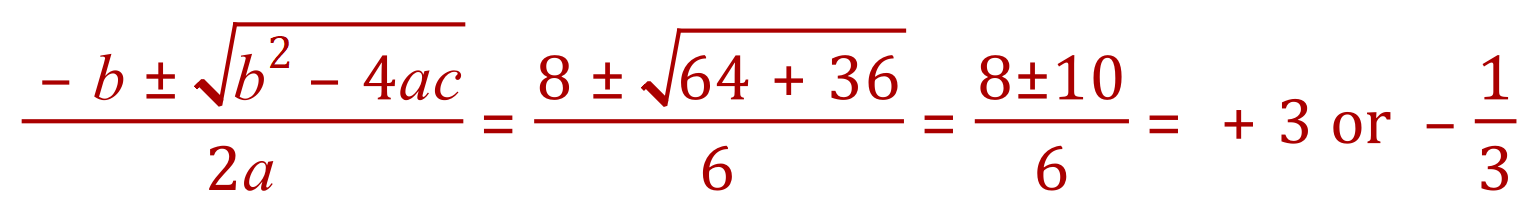
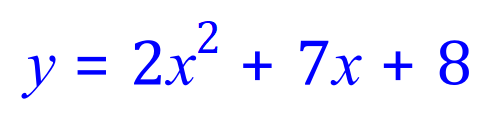
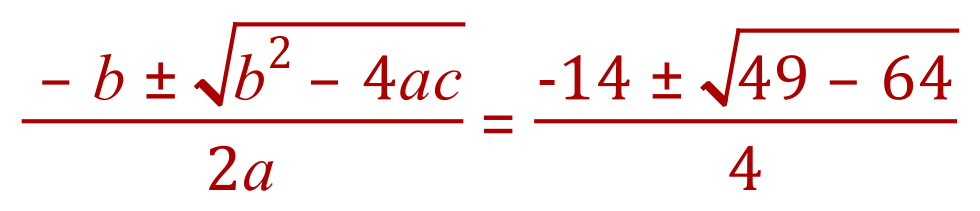
ATTENTION - We can go no further in this third case (not yet anyway) as the expression inside the "square root" is NEGATIVE, and would mean attempting to evaluate the square root of -15. The expression here is called "The Determinant" and has three potential outcomes:
- If the determinant is POSITIVE the quadratic expression / equation will have TWO REAL roots.
- If the determinant is ZERO the quadratic expression / equation will have TWO REAL roots of the SAME value (ie: ONE root)
- If the determinant is NEGATIVE the quadratic expression / equation will have NO REAL roots, it will have COMPLEX roots.
In the above case, the roots would be:
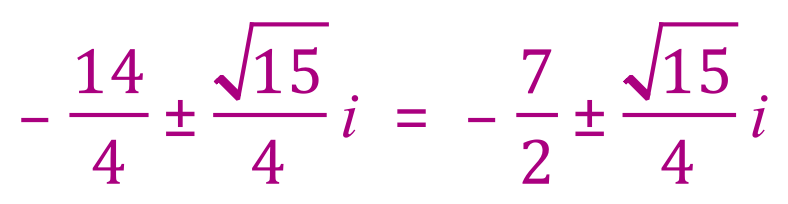
Where:
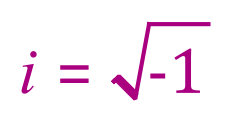
Complex numbers will come up in another section of this book, where the meaning of the entity 'i' will be explained.
Back To >> Questions <<
Back To >> Graphing Quadratic Functions <<