Consider the expression below:

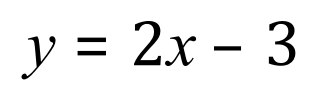
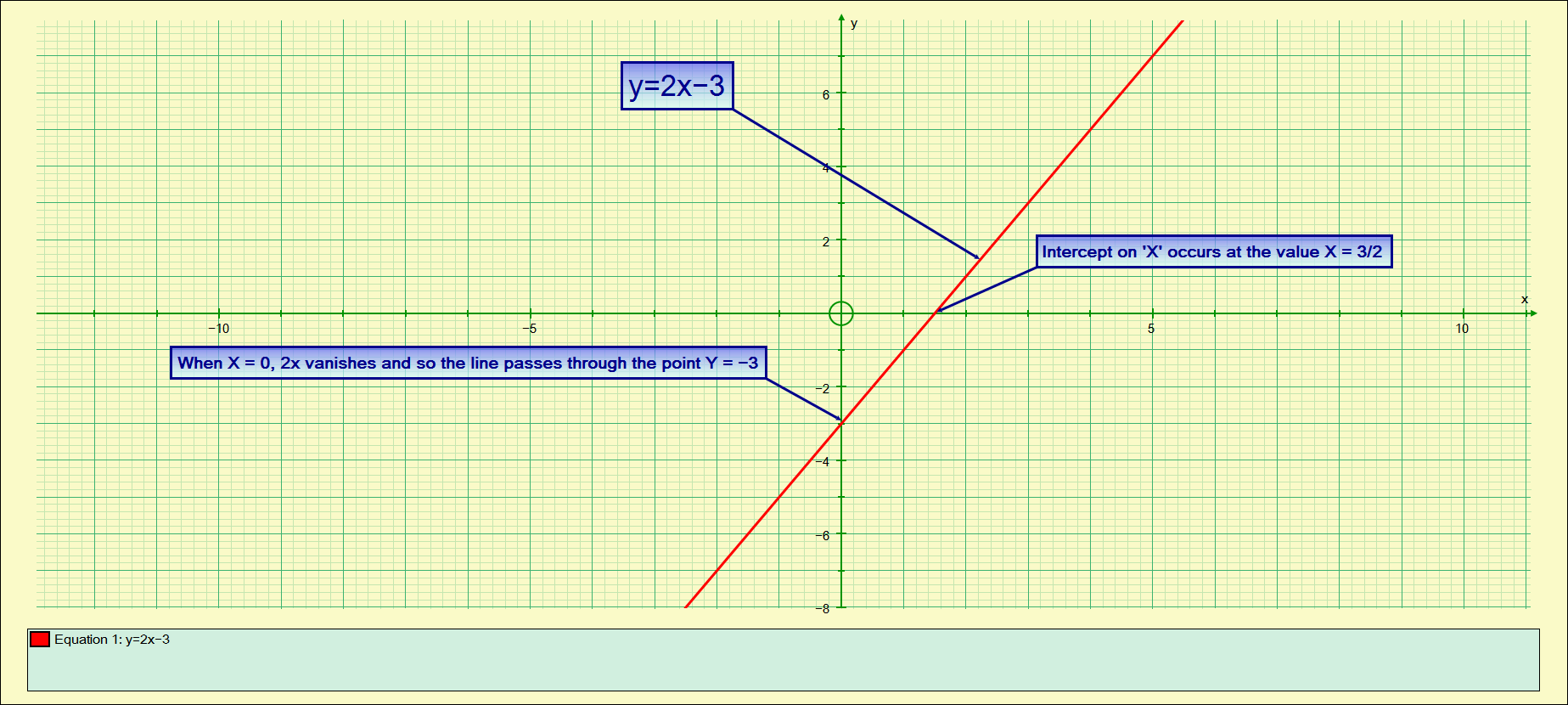
This equation tells us that for every value of ‘x’, a corresponding value for Y will be produced which is equal to 2’x’-3.

X

-2

-1

0

1

2

3

Y

-7

-5

-3

-1

1

3


We can see from the table that there is a point at which the values for Y pass from negative to positive, ie: at some point there is a value for ‘x’ such that the corresponding value for Y is Zero.

Such a value for ‘x’ when Y = 0 is called a “root” of the equation.

Let us now substitute Y for 0:

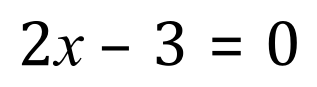
Remembering the “do the same to both sides” rule we can find out a value for ‘x’ which satisfies the equation, ie: which occurs when Y = 0


Add 3 to each side:


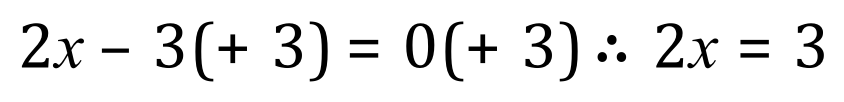
Divide each side by 2:



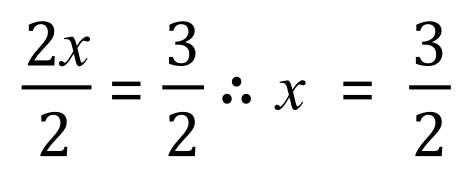
This is a linear equation, if you plotted it as a graph the ‘curve’ would in fact be a straight line according to the generic linear equation

 


These equations are ‘linear’ or ‘first order’ and have only the one root, ie: only the one value of ‘x’ that satisfies the equality Y = 0.

But are there equations for ‘Y= something’ that have multiple values for ‘x’, ie: more than one value for ‘x’ that makes Y=0, that is……more than one root?

Yes……..

Look at the equation below:

 
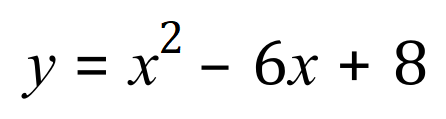
(red below)


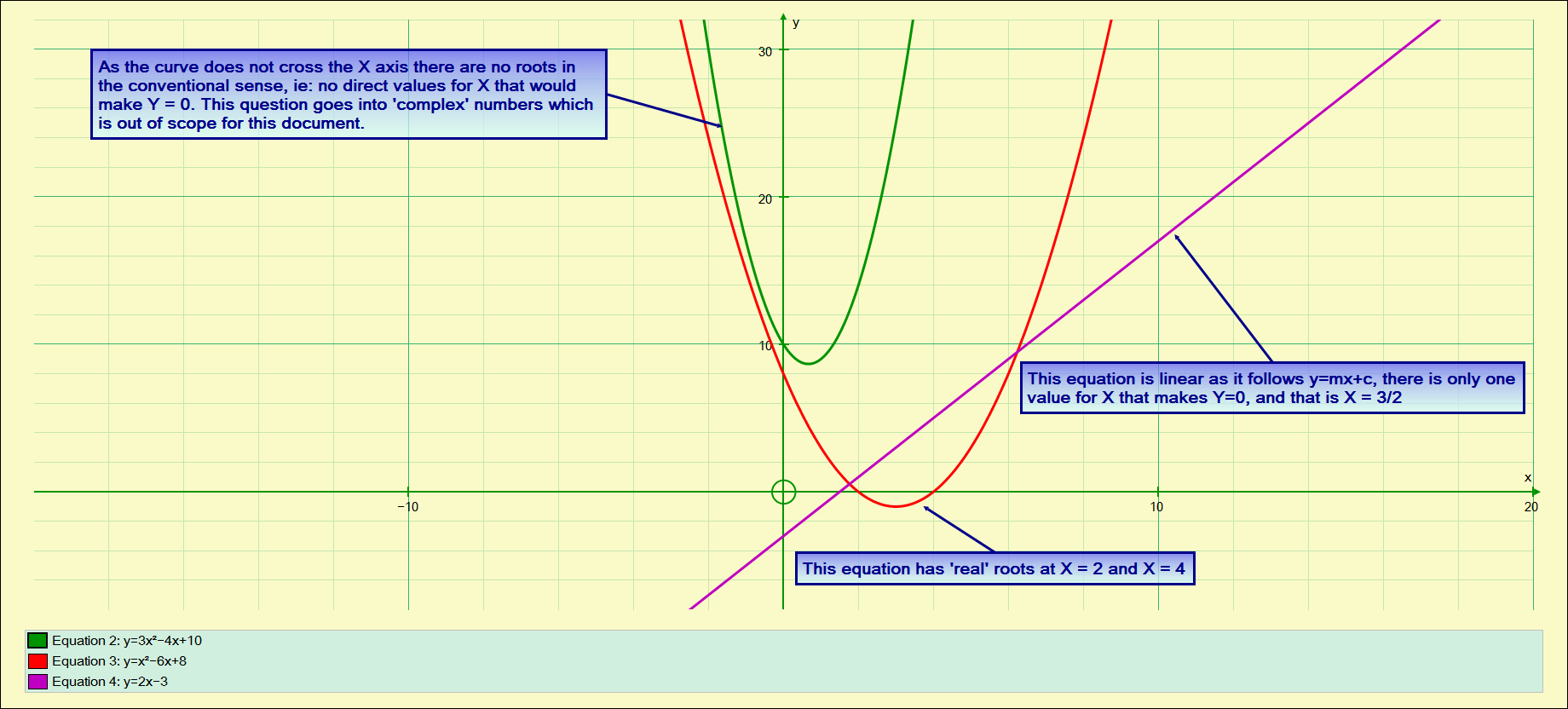
This is a ‘second order’ equation more often referred to as a “Quadratic Equation”. You can of course plot out a table of values and draw a graph, look for the points where the line or curve crosses the ‘x’ axis and this will give your roots…2 of them in the case of a Quadratic Equation (generally, however some Quadratic curves don’t cross the ‘x’ axis so there aren’t any real roots…see the graph above.

Graphing is a good way to locate the roots of an equation, and it is perhaps the easiest way when we look at Cubic (x3), Quartic (x4) etc. equations.

For the time being though, we will stay with Quadratics (x2) and look for ways to find the roots without graphs.

Consider the equation below:

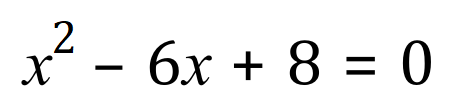
We have graphed this and know that the roots are and because we plotted the curve and looked at the two ‘x intercepts). 

Is there another way to look for quadratic roots?

Yes – in fact three more ways:

  • By Inspection
  • Completing The Square
  • The Quadratic Formula