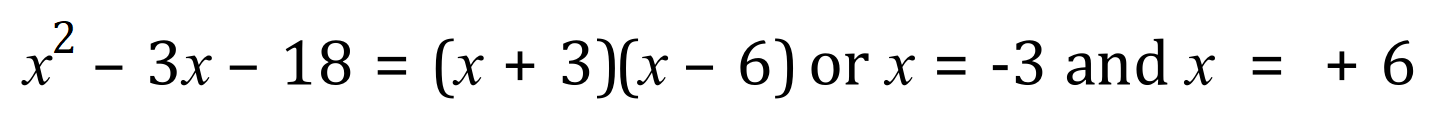OK let’s consider the first way…’by inspection’ – consider the quadratic equation below:

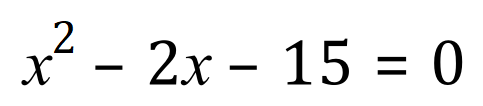
This is a quadratic with real roots (because I chose it that way), but…how do we find them?

Remember …. The roots are those values of ‘x’ that would make the equation equate to zero as expected, and in a quadratic there are generally two.

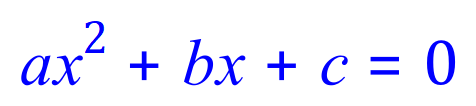
The coefficients are called ‘a’ ‘b’ and ‘c’, in our quadratic problem we need to find two numbers which, when ADDED come to ‘b’ and but which when MULTIPLIED come to ‘ac’.

 Remember that the sign preceding any value of ‘a’ ‘b’ or ‘c’ MUST be included, and that when the quadratic coefficient "a" is not shown, it is 1 and still has to be multiplied by "c" (so "ac" is still required).

OK, back to our problem:

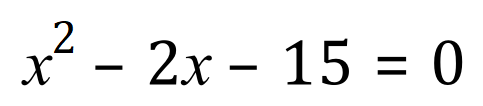
Problem

Possible Responses


Added comes to -2
Multiplied comes to -15


Think of the possible permutations that are factors of 15 as this is the multiplicand


1

15

3

5


OK, study the second pair and drop in a few ‘sign changes’ can you see +3 and -5 fitting the problem?



So, by inspection we see that +3 and -5 will add up to -2 and multiply to -15, so our equation:

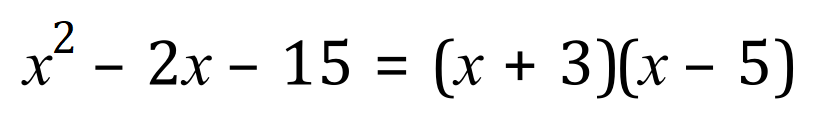
And will produce the curve below, with ‘x’ intercepts (ROOTS) at -3 and +5:


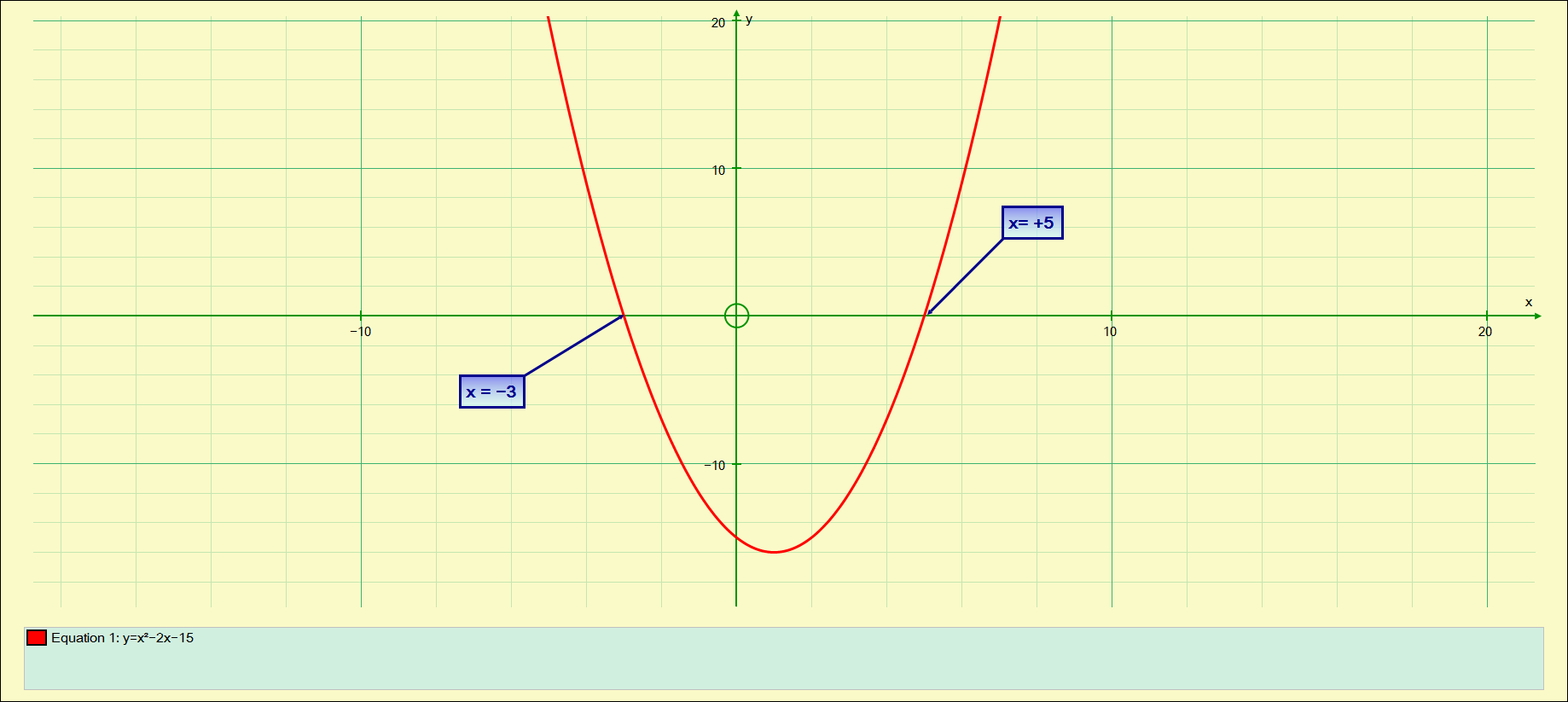
Let’s do another ‘by inspection’ then we can look at ‘Completing the Square’.

Consider this quadratic:

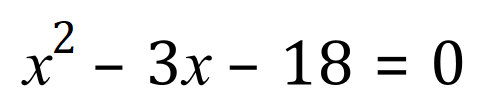
By inspection we need two numbers where A= -3 and M = -18, looking at the factors of 18 we have the possible combinations of:

1 and 18
2 and 9
3 and 6

With a little imagination we can see that +3 and -6 will do nicely, so our quadratic roots will be -3 and +6 (that is, if we were to graph this one, the ‘x’ intercepts would happen at -3 and +6.

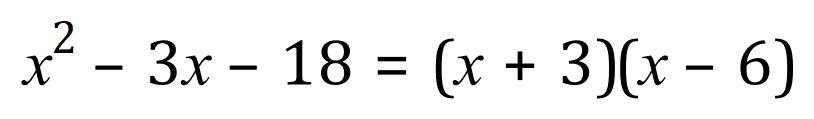
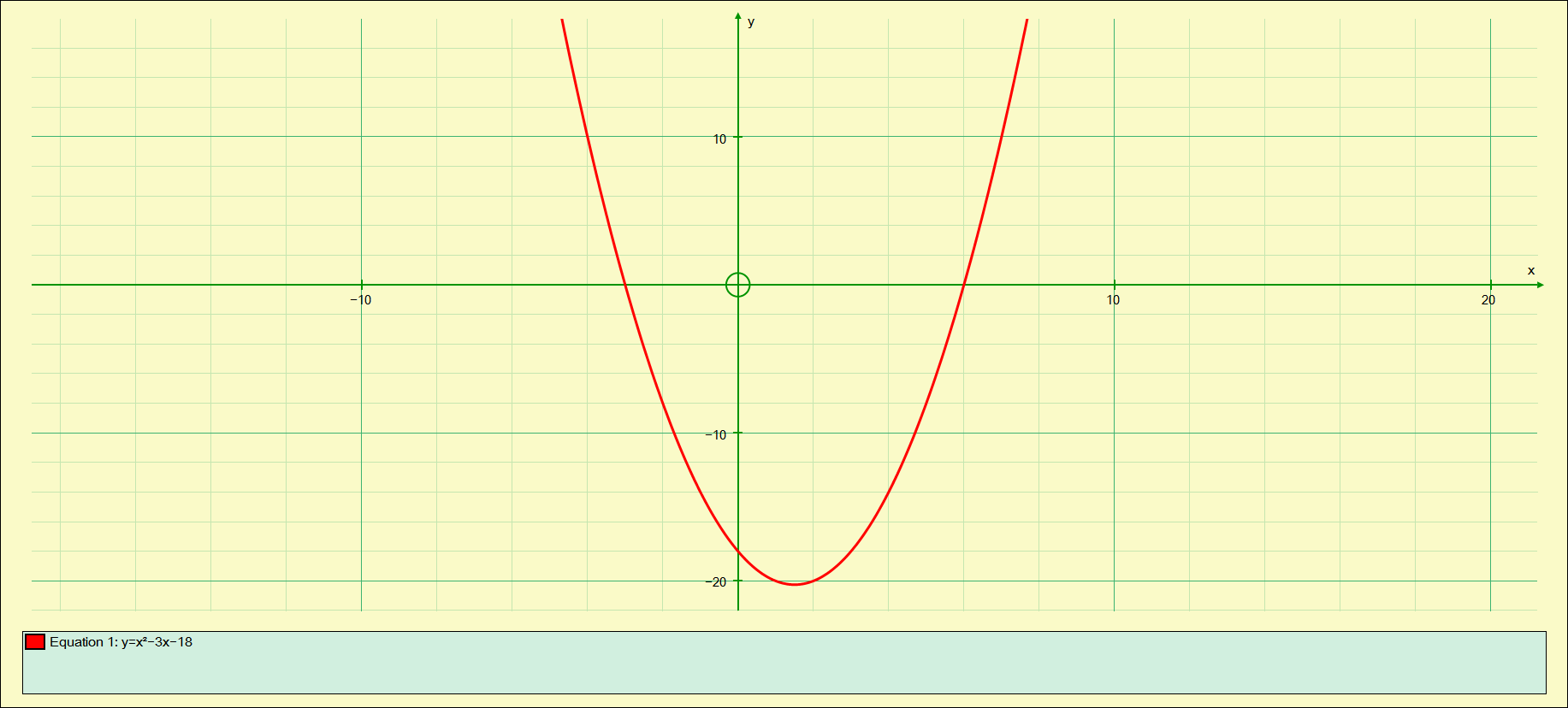
So, by inspection AND by graphing we conclude that the roots of the equation: