When The Coefficient of X Squared > 1
So far, as you can probably see, we have dealt with fairly straightforward quadratics where the coefficient of the ‘x’ squared term (that is the value of the constant ‘a’) has been one.
When the value of ‘a’ is greater than 1 this does complicate matters slightly and we need to look for a way to solve these quadratics.
Take, for example the following quadratic expression:

Perhaps I should mention here that throughout this section I’ve used the word equation rather than expression. To be absolutely correct the above example is in fact an expression because there is no equality, however the expression below is in fact a quadratic equation:
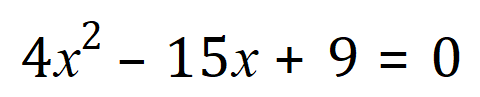
Just to make things clear, if there is an "=" anywhere in the expression it is an equation otherwise it is just an expression. Okay, now that we’ve clarified that let’s go back to our expression:

If you refer back to the general equation for a quadratic:
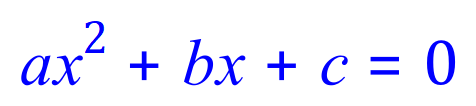
You will see that the value of the coefficient of ‘x’ squared (that is ‘a’) in this case is 4, the value for ‘b’ is -15 minus and the value for ‘c’ is +9. Previously, we have looked for 2 numbers which when multiplied together come to the value of ‘c’ but when added together come to the value of ‘b’. In expressions involving a value for ‘a’ which is greater than one we deviate slightly from this and look for a pair of numbers which, when added together, come to the value of ‘b’ but when multiplied together they come to the value of the products of ‘a’ and ‘c’.

Stop now, and read that paragraph a couple of times until you’re happy that you understand that we are now looking for two values, equalling ‘b’ and ‘ac’ respectively. Let’s take a look at our quadratic expression above, and try to make some sense of this.
As is always the case, at least when you’re looking at the methods I use, restate the problem:

The value for ‘b’ is -15 and the value for ‘ac’ is 36… stop and study this to make sure that you understand why.
So, what possible combination of numbers can we come up with to satisfy these two requirements? Well, if you go through all of the possible combinations between 1, 36 onwards (remembering that you are in fact multiplying these together to make them come to 36) you will quickly find that the 2 numbers that satisfy our requirements are -12 and -3.
So what do we do with them? - Factorisation by Inspection.
As we saw in the previous section, “Factorisation by Inspection” is a skill that should be honed where possible, without needing to resort to graphical means or start drawing boxes all over the place. You should be able to look at the expression, separate the ‘power in ‘x’’ using the ‘b’ and ‘ac’ method above, then by inspection you can then pull out the factors of the expression.
Example 1:
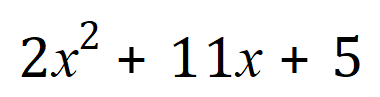
Again, following the method, we need to identify 2 values which, when added together come to +11 but which when multiplied together come to +10. I think fairly quickly you can establish that we are looking at +10 and +1.
Rewriting our expression we have this:
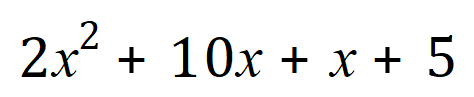
(remember that ‘x’ is in fact ‘1x’)
Separating the right-hand side into 2 blocks:
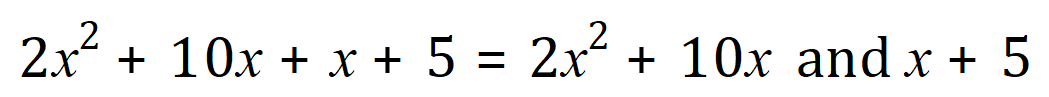
we now factorise the expressions that we are left with:

in this particular example you can see that x+5 doesn’t really change, the reason I put one in front of it is that when we come to pair up the factors will need something to go along with ‘2x’
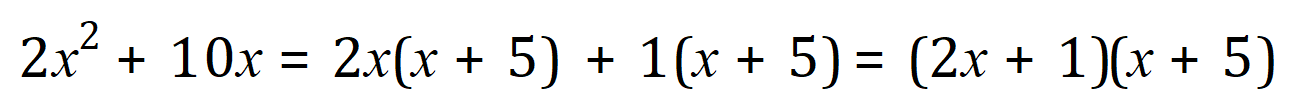
And as you can see, we have now arrived at our factorised expression.
Example 2
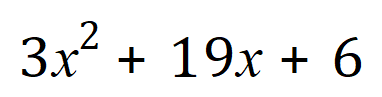
In this particular instance we need to find 2 numbers which, when added together come to +19 but which when multiplied together come to +18. Clearly +18 and +1 will fit the bill quite nicely.

In the same way that we did for the first example, we “pair off” and factorise:
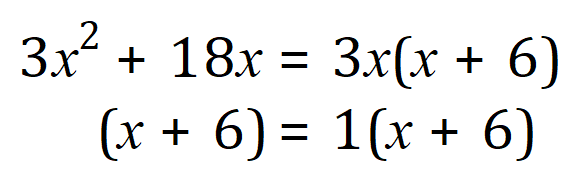
As you can probably see this example is working is almost identically to the first one, and I have preceded the right-hand side of the second expression with a single number 1 for exactly the same reason.
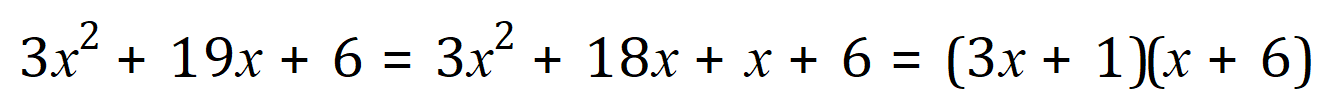
Once again, we have arrived at our factorised expression.
Example 3:
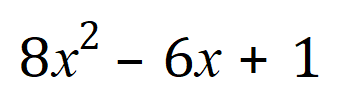
In the same way as in the previous examples, we now need to look for two values which when added together come to -6 but which when multiplied together come to +8. Giving this a little bit of careful thought you will come to the conclusion that -4 and -2 will do it.
Rewriting our expression:

And, in just the same way as before, we now “pair off” and factorise:
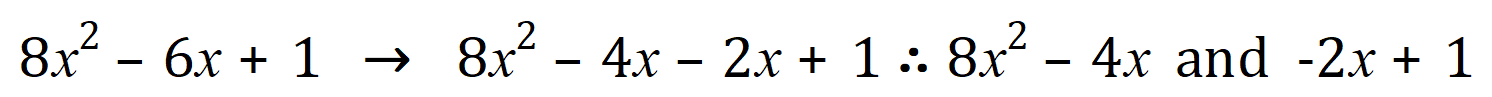
Don’t forget to pay careful attention to the signs, in the 2nd expression it is indeed -2x and not simply 2x.
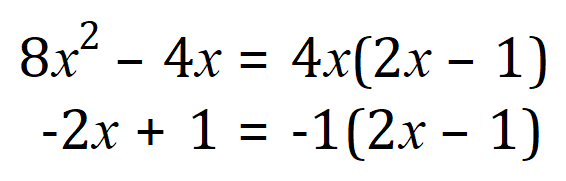
Gathering of the results we now factorise our expression:
Go To >> Questions <<
Go Back To >> Maximum Volume of a Box <<