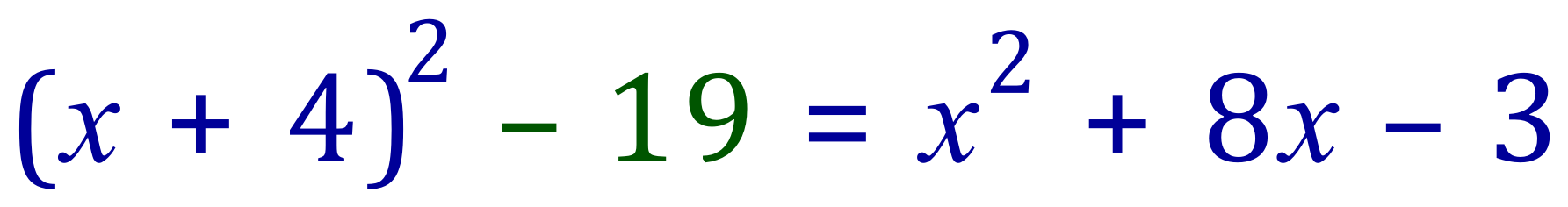Completing The Square
The formula in elementary algebra for computing the square of a binomial is:
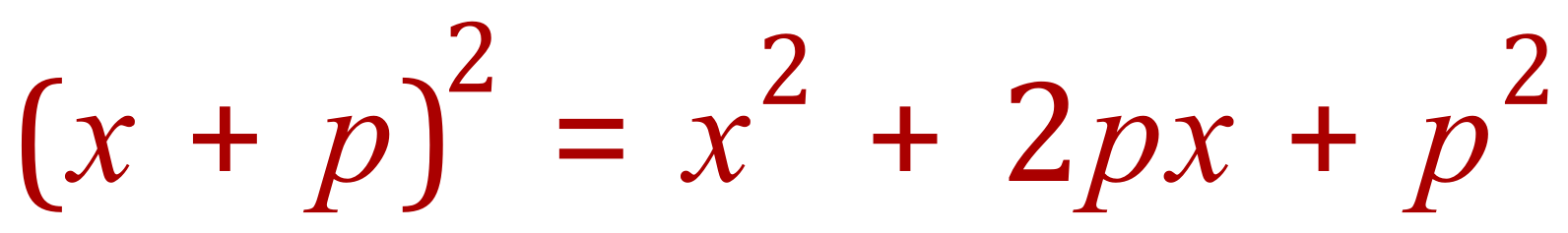
For example:
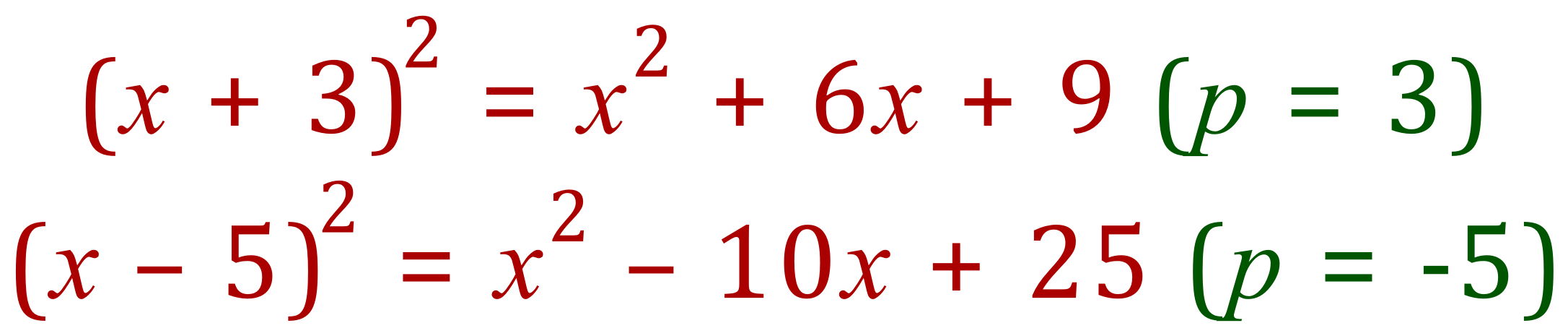
In any perfect square, the linear coefficient of x is twice the number p, and the constant term is equal to p2. Consider the following quadratic polynomial:

This quadratic is not a perfect square, since 28 is not the square of 5:
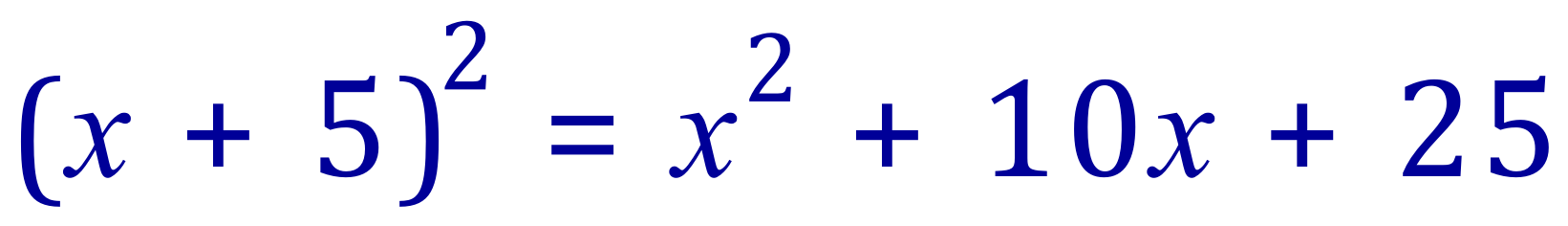
However, it is possible to write the original quadratic as the sum of this square and a constant:
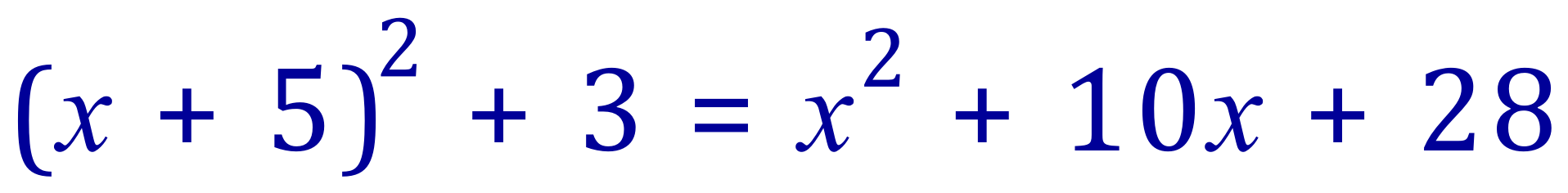
This is called completing the square.
What is a "Perfect Square" ?
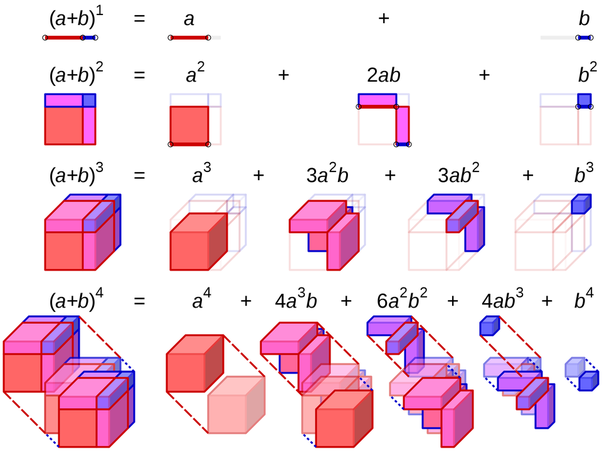
It can sometimes be easier to visualise with an image, certainly in the first three cases here, although when we reach the quartic term it's not so easy.
Where the quadratic term is not a complete square, we have to add or subtract from the expression to make it so. Let's have a look at a few examples:
Example 1:
Make the following quadratic expression a perfect square by completing the square:
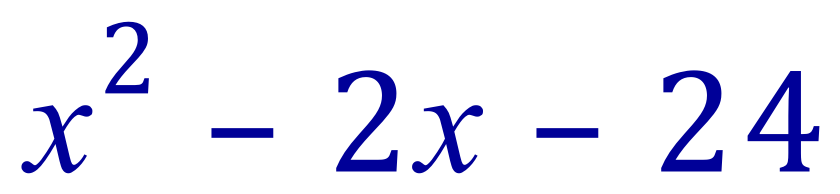
Extract the square term as it stands and expand it (halve the linear coefficient):
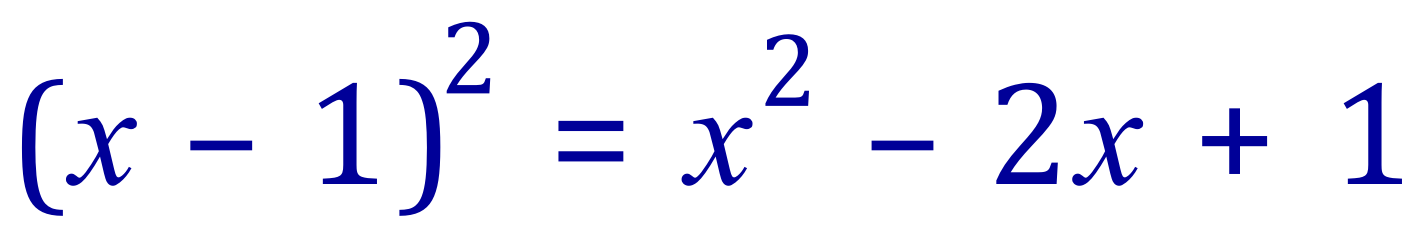
The constant term is now +1 but started off as -24. We therefore need to subtract 25 to complete the square:

Example 2:
Make the following quadratic expression a perfect square by completing the square:
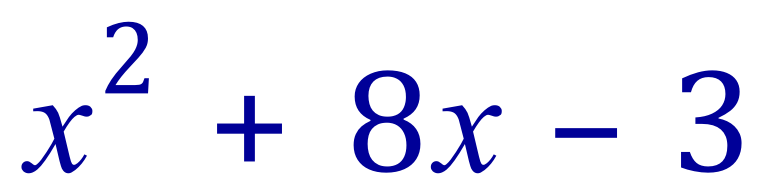
Extract the square term as it stands and expand it (halve the linear coefficient):
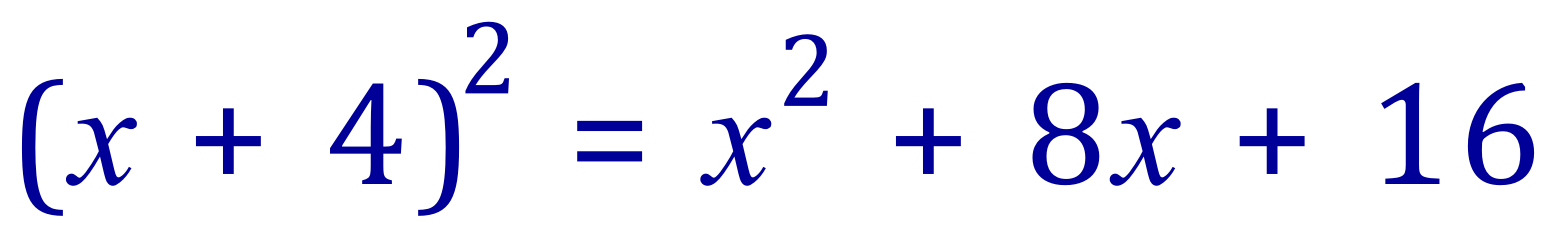
The constant term is now +16 but started off as -3. We therefore need to subtract 19 to complete the square: