Solving Quadratics by Completing the Square
Probably a method that you won’t use that much, but useful to know anyway. This is another way to solve a quadratic equation if the equation will not factorise (but can be used in any event). It is often convenient to write an algebraic expression as a square plus another term. The other term is found by dividing the coefficient of x by 2, and squaring it. Any quadratic equation can be rearranged so that it can be solved in this way.
Have a look at this example………
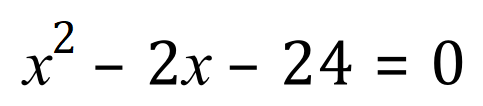
By inspection we can see that A = -2 and M = -24 so our values of ‘x’ would be -6 and +4 giving roots of 6 and -4 but completing the square gives it this way:
Step 1 - Restate the equation (always a good idea):
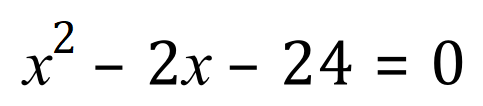
Step 2 - Rearrange to get the x terms on the left and the numerical term(s) on the right:
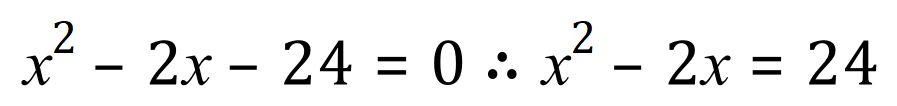
Step 3a - Halve the coefficient of ‘x’, then square it and add to both sides:
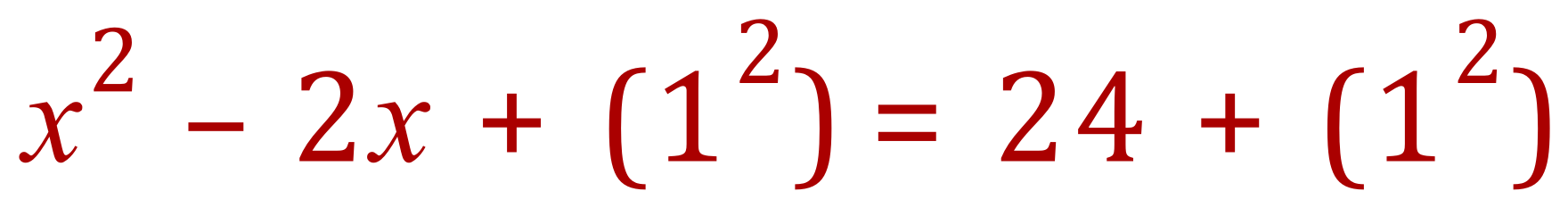
Step 3b - Understand where the next step comes from (expand the RHS to make sure you see that it is the same as the LHS):


Step 4 - Take square roots:
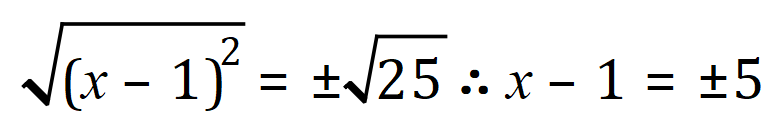
Thus…..
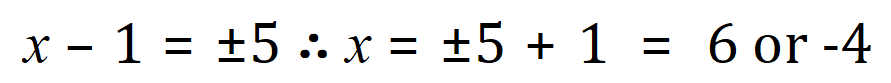
And so these are our roots of the quadratic equation.
The reason that I have shown Steps 3a and 3b in red AND in two parts is that sometimes students and teachers "jump" this step in their "working", which is OK if you understand why. It is best to include it until you are really confident in this type of algebra.
Have a look at these examples (note that the solution to the last one shows the roots in SURD form, i.e. as a result with a square root component):
Example 1:
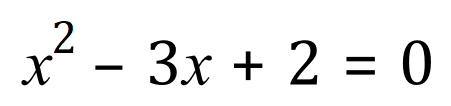
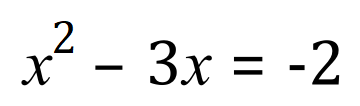
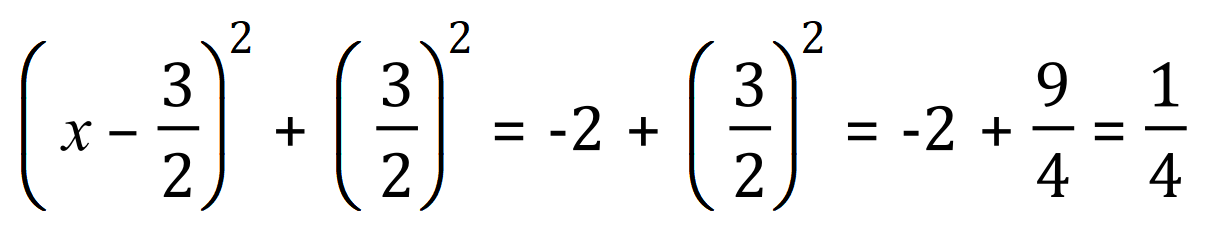
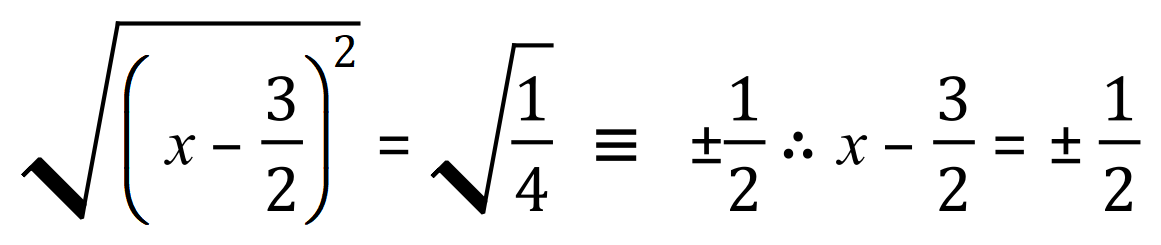
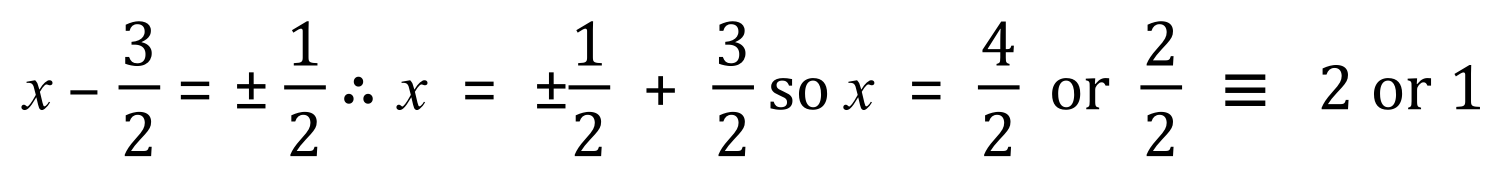
Example 2:
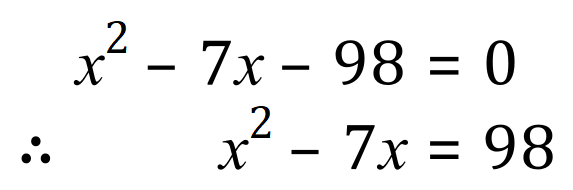

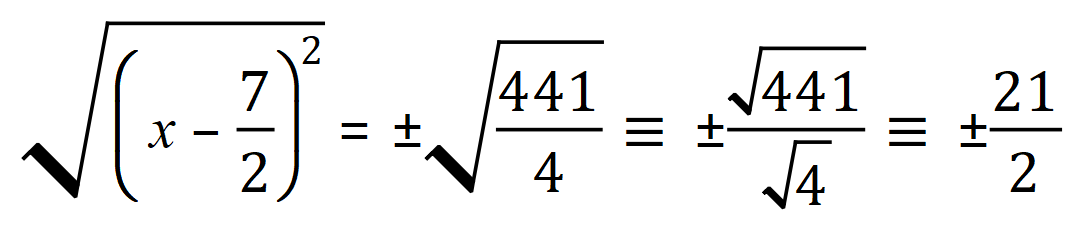
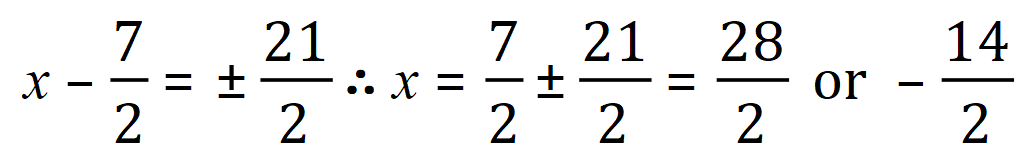
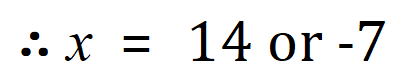
Example 3:
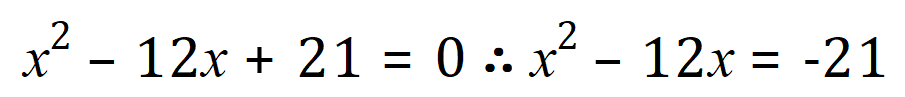

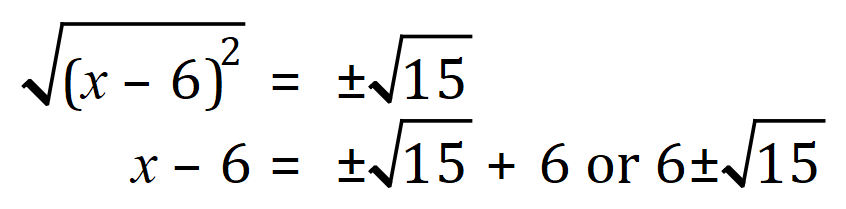

Note that the answers here (in Example 3) are left in SURD form as they involve square roots. This is often done where an exact answer is requested, and working out the decimal or fractional equivalent would only render an approximation. Let me explain further:
If we take the equation that we have just found the roots for, and plot it on a graph, we will see the X axis intercepts at the point of the roots. These appear to be at approximately 9.87 and 2.13.....
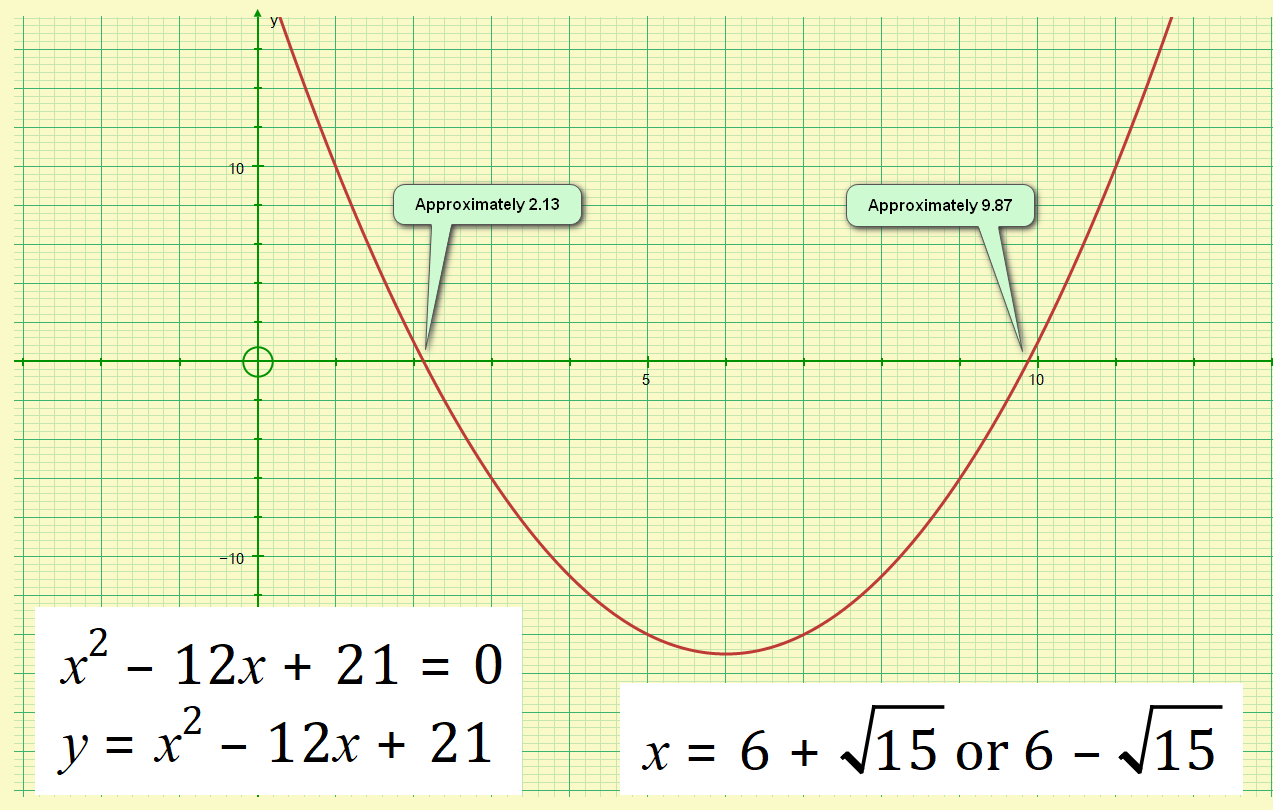
However, these can only be approximations because the square root of 15 is not a rational number. For convenience I have quoted the approximate roots to 2 decimal places but irrespective of the number of decimal places I choose, I cannot ever arrive at an exact value. This is where "surds" come in because leaving the number inside form leaves it in an exact form.
If you need further convincing, consider "what is the square root of two"?, While off the top of my head I can tell you that approximation for it is 1.414 (or of course -1.414) this is only accurate to 3 decimal places.
My computer calculator gives it as:
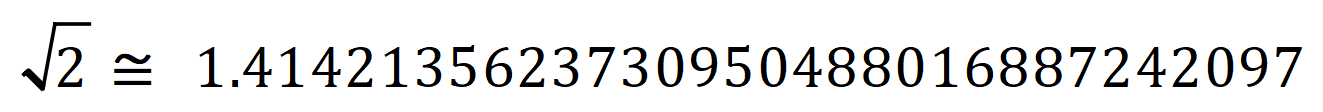
And although this appears to be impressive, it is still only an approximation. The only way we can state exactly the square root of two is to leave it in surd form.
We will meet surds in another part of this document.
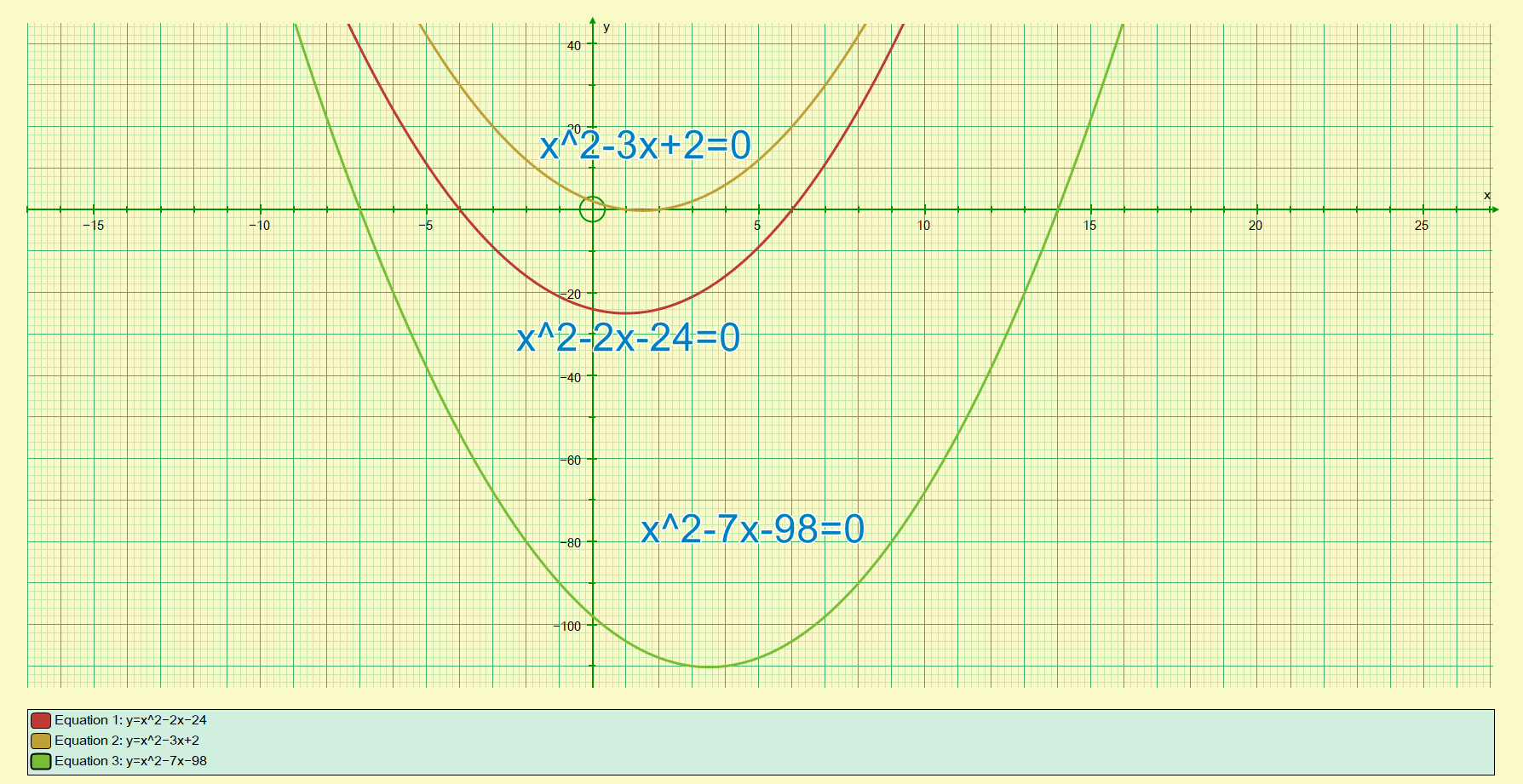
Here are our three equations as graphical plots, note where the curves cross the "x" axis, these are the roots of the equations.
Completing the Square can be a bit fiddly, it’s probably not the favourite method especially under the pressures of an examination setting. It is likely that the “Quadratic Equation” would be given and requested.
>> Questions <<
Back To >> Solving Quadratics by Completing the Square (S) <<