The Quadratic Equation / Expression / Formula
Although ‘Completing the Square’ isn’t the simplest way to obtain the roots of a quadratic, it does lead to the deduction of a general equation to solve them.
The equation / expression / formula is probably very familiar to you:
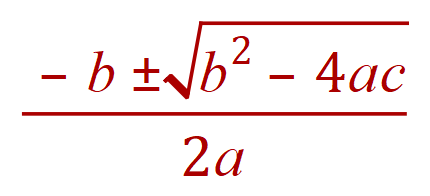
If possible this produces the two roots of your quadratic equation (one from the PLUS part of the square root expression, and one from the MINUS part). If there are no real roots a complex result will occur (if the square root part turns out to be negative). In this document I have avoided complex numbers.
OK so how does Completing the Square lead to the ‘famous’ quadratic formula?
Let’s look at the general formula for a quadratic equation:

We can divide the whole thing by the coefficient of x2 to produce (although you mightn’t agree) a ‘simpler’ quadratic:
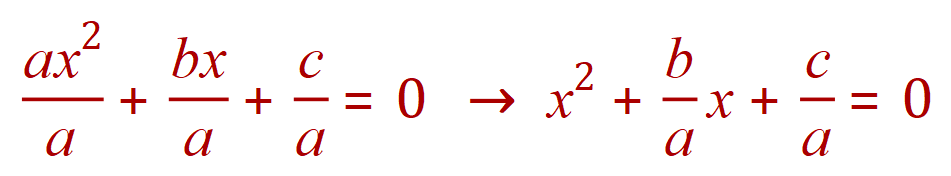
Now we start the ‘complete the square’ process by moving the constant value across to the right hand side of the equation:
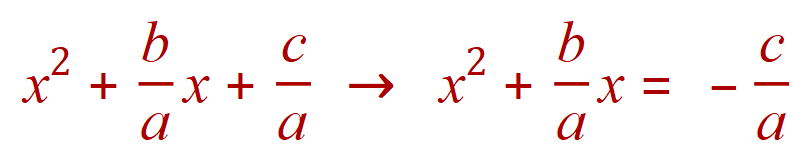
In the same way as before, we halve the coefficient of the ‘x’ term, square it and add it to both sides:

So:
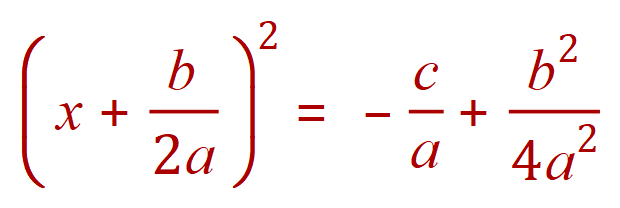
We simplify the right hand side by entering a common denominator and adjusting the numerator to suit:
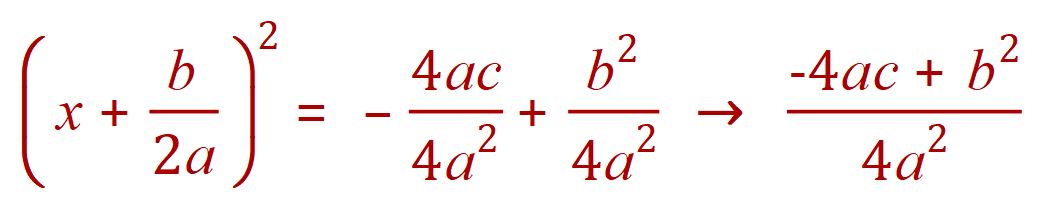
Rearranging (a little) :

Taking square roots:

Therefore:
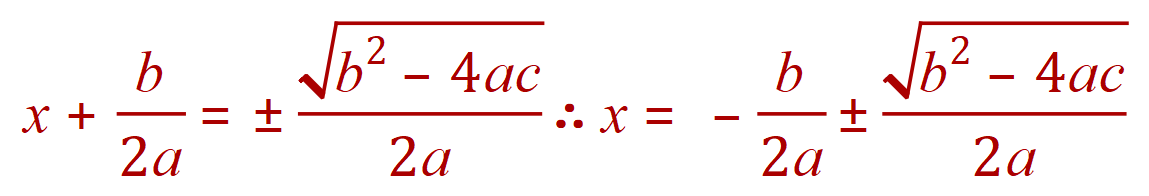
Finally:
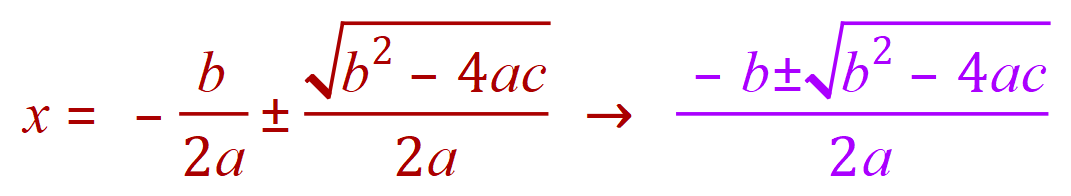
Example 1:
Now that we have derived the equation, let’s have a go at solving a quadratic that we already have the roots for:
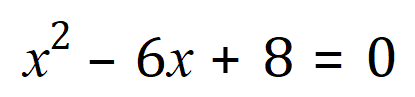
We already know that ‘x’ = +4 or +2, but let’s ‘derive’ these from the equation:
Looking at the equation we can see that the relevant values of a, b and c are +1, -6 and +8 respectively
If you are unsure, stop here and have a think about the ‘generic’ equation above.
So if we ‘plug’ these values into the quadratic equation we have:
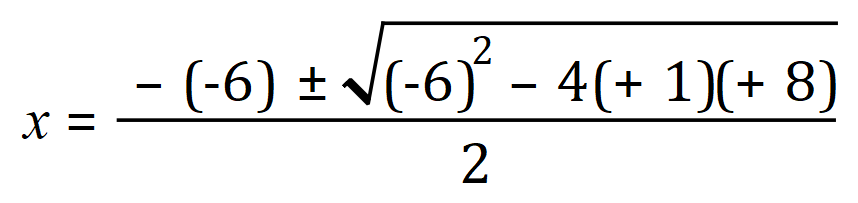
Again, stop and study this to see where the values all come from, note that as ‘b’ is negative we must remember to include the sign.
So:

Example 2:
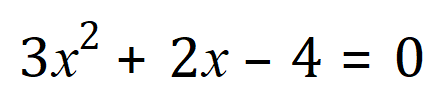
From the equation we can see that the values of a, b and c are +3, +2 and -4 respectively, so…using the quadratic formula:
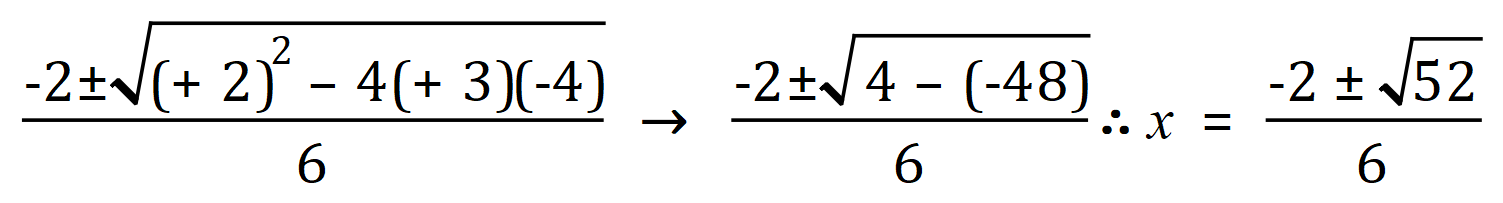
To simplify the SURD using prime factorisation, we establish that:
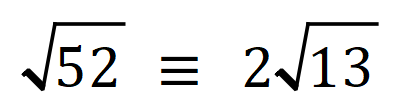
so the expression now becomes:

Therefore our roots of the equation:
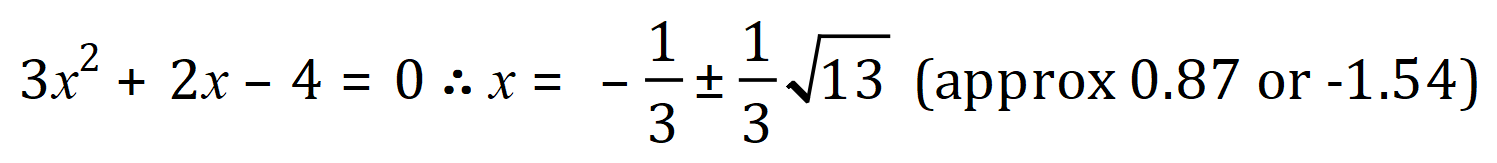
Normally in such cases you would report the result in SURD form, because the roots are in fact irrational numbers and any amount of decimal places would be meaningless.
Here is the graph of our two example questions:
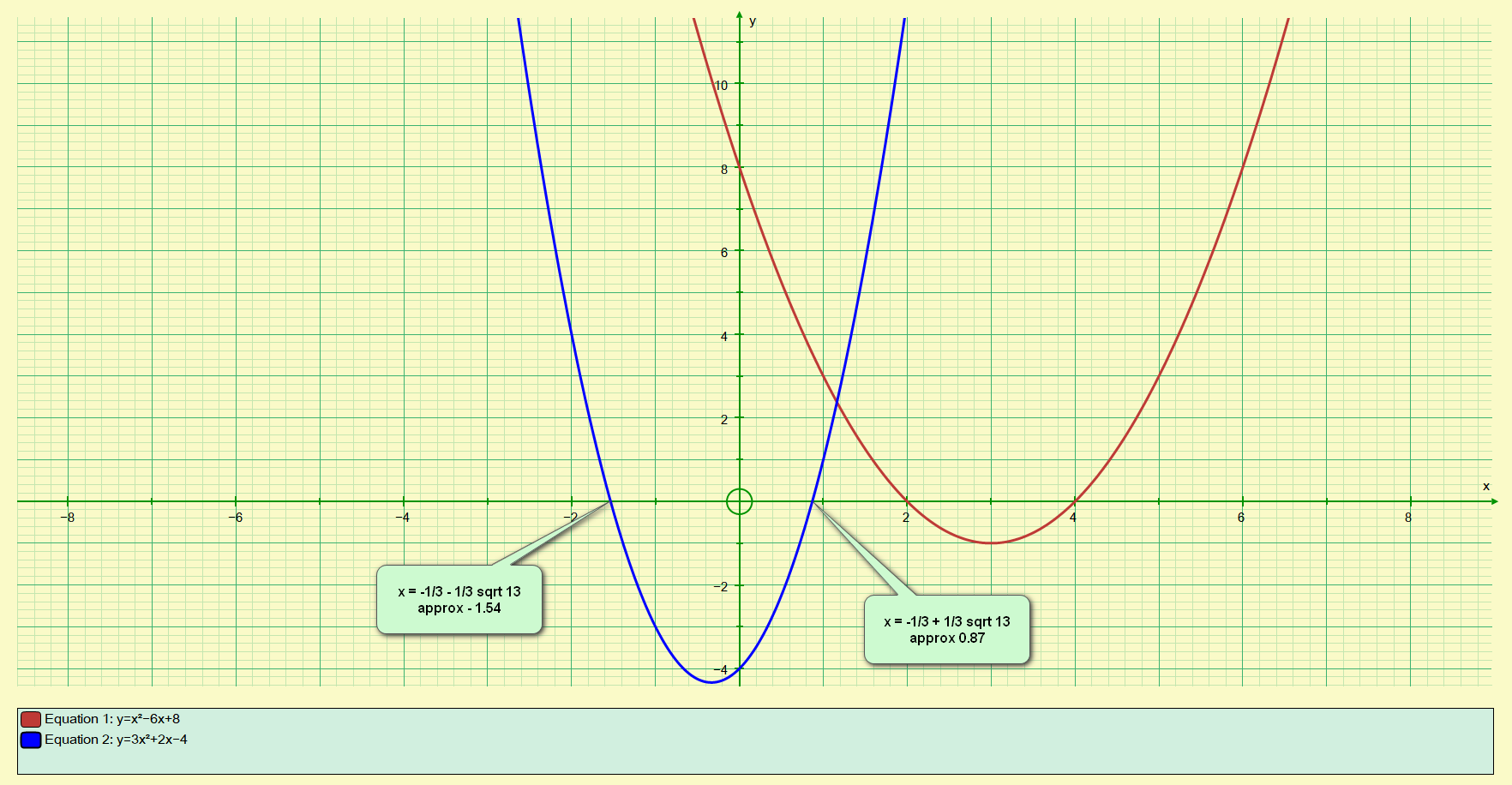
Drawing a graph of a quadratic function is an alternative method to establish the roots of the quadratic function itself. Although usually the "quadratic equation" is used, graphing can also produce a desired result.
Go To >> Graphing Quadratic Functions <<