Quadratic Equations With Complex Roots
In the previous section on quadratic equations, and quadratic expressions we were introduced to several methods of solution, one of which was the “quite well known” quadratic equation formula:
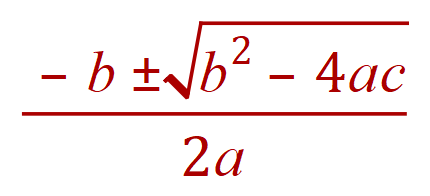
Where ‘x’ represents the roots (of which there may be 0, 1 or 2) and the letters ‘a’ , ‘b’ and ‘c’ represents the coefficients of ‘x’ squared, coefficient of ‘x’ and the constant respectively, so for example in the expression below:

The value for ‘a’ would be +2, the value for ‘b’ would be +5 and the value for the constant ‘c’ would be -7.
It is imperative that you get the signs right because you’ll be putting these values into the quadratic formula and if you get your signs mixed up you can go horribly wrong. Using the example above, just for the sake of simplicity we can solve the equation and determined that in this particular case there are 2 distinct real roots, their values are +1 and -3.5 respectively (if you substituted either of the values into the equation you will see that this is in fact the case:
With x = 1:
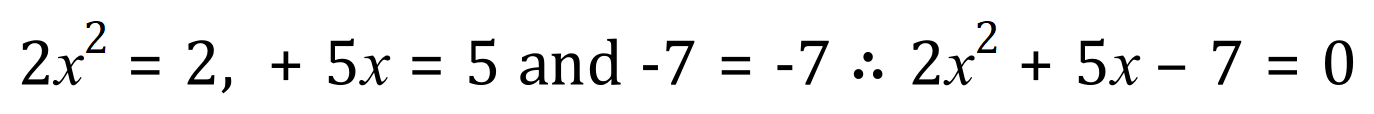
With x = -3.5:
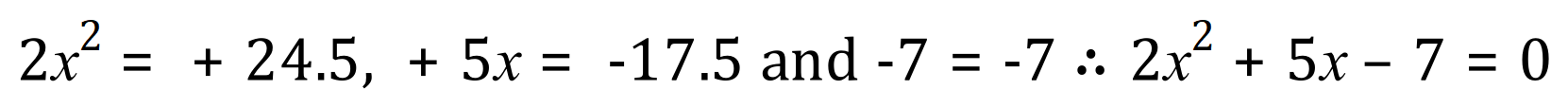
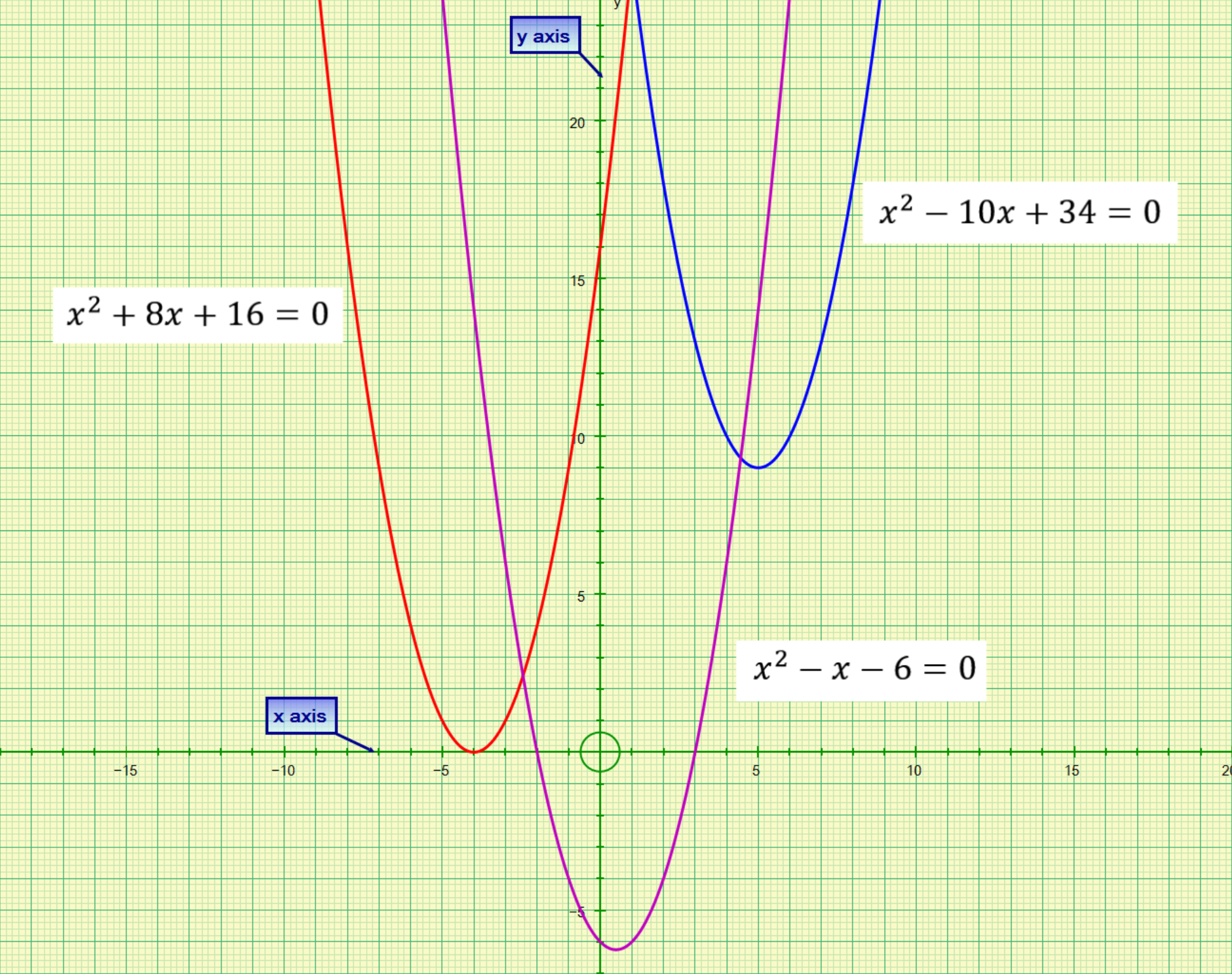
So in this very simple case we have proven our roots to be correct. Unfortunately life, especially mathematical life, isn’t always this simple and the roots can be considerably more complicated than this. In certain cases the roots will be identical, this would occur where the quadratic equation, when plotted, touches the x-axis at the apex of the curve, as opposed to intersecting it into distinct places as would be the case in the example above where we have 2 real roots.
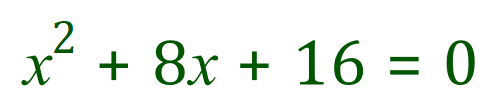
This quadratic equation is such an example, because if you factorise it you will see that ‘x’ equals -4. The curve of such an equation does not intersect the x-axis, it merely touches it at the appropriate point (see the graph).
You may recall from an earlier discussion on quadratic expressions and equations that the deciding factor as to whether or not the quadratic will have 2 real roots, one real root repeated or no real roots depends on the value of that part of the equation which lies beneath the square root symbol, known mathematically as the “determinant”:
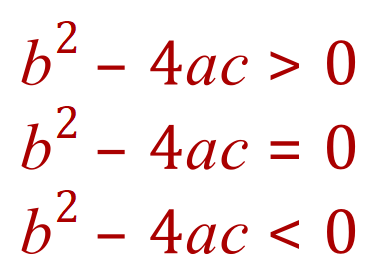
If the determinant > 0 : If the value of the determinant is positive, then the quadratic expression will have 2 real roots.
If the determinant = 0 : If the value of the determinant is 0, the quadratic expression will have one root repeated twice, or if you like ...two identical roots.
If the determinant < 0 : If the value of the determinant is negative, the expression cannot have any real roots because this will involve taking the square root of a negative value.
Note that in the last case I said "cannot have any real roots", not "cannot have any roots" as there are roots to such an equation but "it's complicated" 8-)
Mathematicians are a funny breed and they don’t normally like being told that something is not possible, so if they can they will make it possible, even if this means inventing something...........
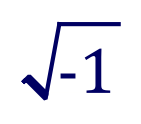
We said earlier that you cannot take the square root of a negative number; that is until now anyway you've been told that you can't. That's because you had no numbers which were negative after you'd squared them (so you couldn't "go backwards" by taking the square root). Every number was positive after you squared it. So you couldn't very well square-root a negative and expect to come up with anything sensible.
Now, however, you can take the square root of a negative number, but it involves using a new number to do it. This new number was invented (discovered?) around the time of the Reformation. At that time, nobody believed that any "real world" use would be found for this new number, other than easing the computations involved in solving certain equations, so the new number was viewed as being a pretend number invented for convenience sake.
This number was given the letter i and it is equated to the square root of -1:

The ‘i’ stands for ‘imaginary’ because this construction, as mentioned above was never meant to be real, just a convenience to make mathematics simpler. Based on the above you should be able to see that:
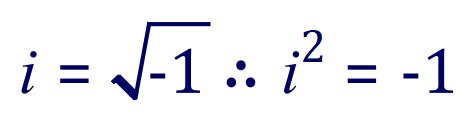
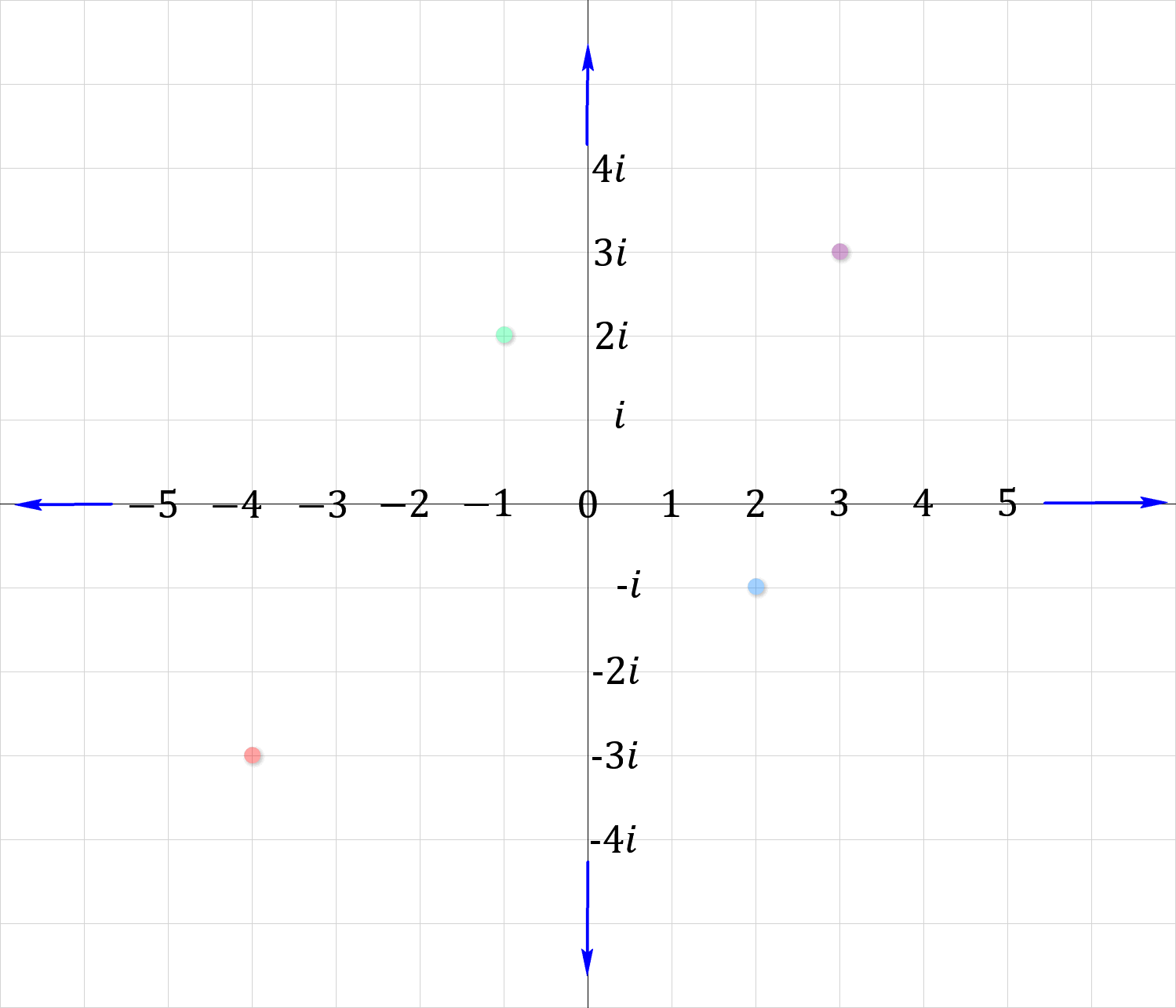
To complicate things even further, mathematicians decided that they would need to multiply these imaginary values by real numbers in the various calculations that they were going to use them in. This effectively added a second dimension to the one-dimensional number line that you have become used to during your mathematical development. If you remember the number line is shown as a horizontal line starting at 0, extending infinitely to the right with the positive values and infinitely to the left with a negative values. Now imagine a vertical axis passing through the 0, extending vertically to infinity with positive values of ‘i’ (upwards) and likewise vertically to infinity with negative values of ‘i’ (downwards).
Technically then, every real number which, until now we have regarded as one-dimensional, should now be represented as a two-dimensional number based on its value and an appropriate number of ‘i’ increments added or subtracted.
So, in the graph above, the points shown are:
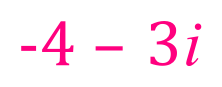

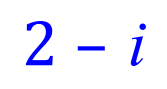
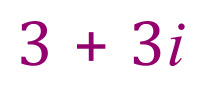
So how we actually "solve" such quadratic equations? Well you might be surprised to learn that these equations are not really much more complicated then their "real" counterparts, all you need to remember is a little bit of arithmetic trickery concerning surds, then you will be well placed to solve this sort of equation.
Remember that a surd is a "square root" representation of a number, so:

Is in fact a surd, the square root of two which is the length of the hypotenuse of a right angle triangle where the other sides are one and one respectively, if you cast your mind back to that section you will remember that we cannot quote the length of the hypotenuse to an exact number of decimal places because the square root of two is an irrational (infinitely long) number.
If you take a look back at the surd section you will see that we can use prime factorisation to try to simplify a surd, the example you will see will be the square root of 175 which ultimately simplifies by prime factorisation:
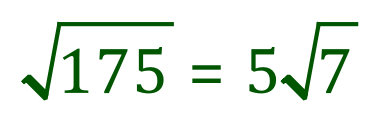
However, before we reached this final point we passed through a number of intermediate stages which showed that numbers in square root form can be made up as the product of the prime factors in square root form, so for example before we reach our final answer as shown we would have seen this:
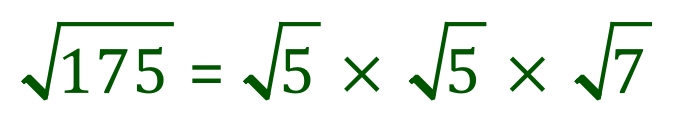
So if you think about it we should be able to take any number and represent its square root as the product of the square roots of two (or more) of its factors as above. Now let us take this one stage further, look at the number shown, can you see the validity what I have written?

We can indeed take the positive number 49 and by multiplying it by -1 effectively invert its sign to make it negative. Now, consider this:
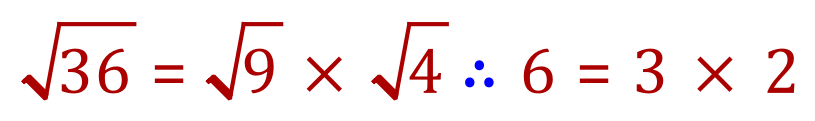
We can take a number such as the square root of 36, and simplify it by showing it as the product of the square root of nine multiplied by the square root of four. As you can see, six does in fact equate to three times two.
What about if we now bring on board our newly invented entity "i" which we have already given a value of the square root of -1
If what we have said above is true, and we know it is, then can we say this?

If we now substitute the value for the square root of -1, and the value for the square root of +36 we can finally state:
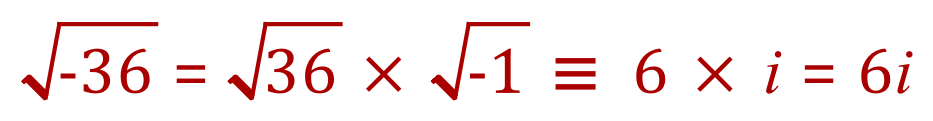
So we arrive at a result that you previously thought could not be done, and can declare that the square root of -36 is in fact the complex number 6i
We can now "weave" this arithmetic trickery into solving some quadratic equations where the determinant is negative, that is where the bit contained underneath the square root symbol is negative and so previously we would not have gone any further with it, now we can !
Example:
Let's take a look at the following simple quadratic equation which is been deliberately chosen because it does not have any conventional roots:
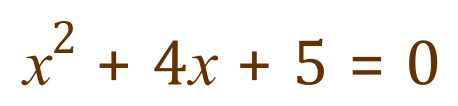
We use the "quadratic equation" substituting a=+1, b=+4 and c=+5:
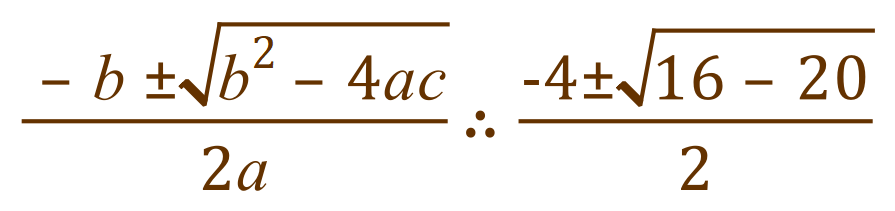
We can see straight away that the determinant is going to be -4, because 16-20 does in fact make -4. Previously this would have stopped us, but now we carry on:
Remember:
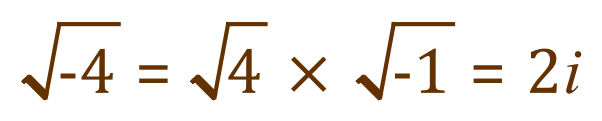
So the "complex roots" of the quadratic equation will now become:
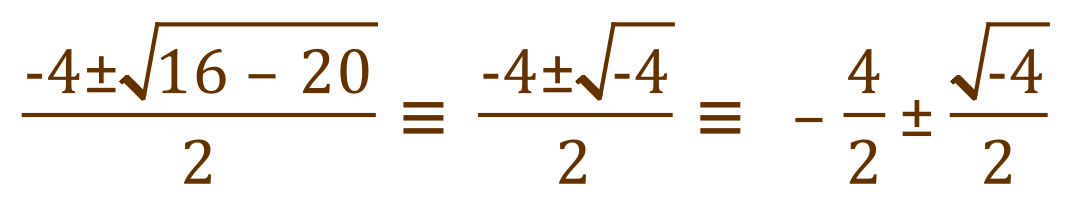
Substituting for 'i'
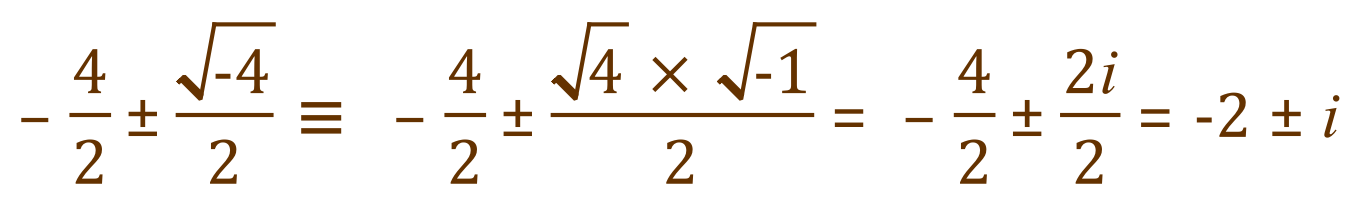
So the complex roots of our initial quadratic equation are:

>> Questions <<