Surds
When we complete any calculation in mathematics we are normally asked to quote the answer either to a certain number of significant figures or a certain number of decimal places. Where the answer is a fraction we are usually asked to quote it in its simplest form.
When the answer is a square root however, a certain amount of accuracy will always be lost if we are then forced to quote this answer to a certain number of places, as a result it is quite normal to leave the answer in its “square root” or “roots” format. This is a known as “Surd Form”
A small example might help at this point to make it obvious why we would need to do this:
Consider the right angled triangle below:
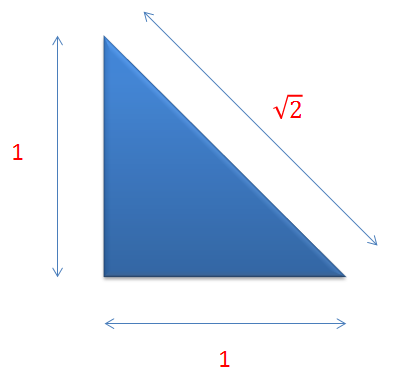
We can see that two of the sides have a length of one unit, and using “Pythagoras theorem” we can work out the fact that the hypotenuse will have a value as shown. At this point we have two choices:
- quote the length of the side of the hypotenuse to whatever accuracy is desired, i.e. a number of decimal places, or
- leave the result as it is shown above
If we consider the first option we can see that the square root of two is in fact 1.414 to 3 decimal places but this is not “the square root of two”, it is only an approximation of it. In fact, because the square root of two as a decimal number is irrational (that is, it has an infinitely long decimal part” no matter what accuracy you quote it to it will never be exact. This is why the second option, “leave the result as it is shown above” or “leave the result in surd form” is preferable, because it is an exact representation of the answer.
Since surds can appear in any size, we must devise ways in which we can make them simpler.
One of the ways of doing this is to repeatedly divide by prime factors starting at 2, then 3, then 5 until you’ve gone as far as you can. Generally these results are written down in a sort of “family tree” descending hierarchy which I call a “prime factor tree”.
Example: Let us suppose that the result of a calculation we have made leaves us with the following surd:

It may be that this is an acceptable format to leave the answer in but generally you would do something to try to reduce this, or make it simpler.
Consider the number, not as a square root, but simply as the number 175.
Step One: identify the first prime factor that will divide into this number. As it is an odd number we know that 2 will not divide into it, for that matter neither will the next available prime factor 3, in fact the first available prime factor to divide into this number is 5 so we divide 175 by 5 leaving 35.
Step Two: we can see that 35 also divides by 5 leaving 7 so our prime factors of the number 175 can be shown like this:

175 is not in fact the number we are dealing with however, we are dealing with the square root of 175 and so we now have to bring into play one of the rules with regard to surds:
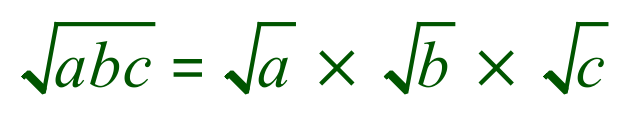
So if we substitute our numbers into this rule:
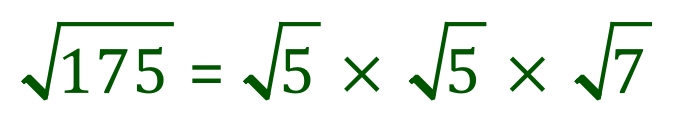
You should be able to see that “root five” multiplied by “root five” is in fact five, so the above expression simplifies now to this:
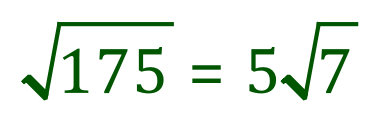
Example: let us again suppose that the result of a calculation leaves us with the surd:
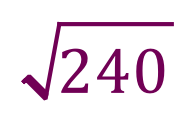
And we wish to simplify this is far as we can. Once again, consider this number as 240 not a surd:
Step one: using the first prime factor (2) divide 240 leaving 120.
Step two: 120 is an even number so once again we can divide by 2 leaving 60.
Step three: we can once again divide 60 by 2 leaving 30.
Step four: we can divide 30 x 2 leaving 15.
Step five: we can divide 15 x 3 leaving 5 and this in fact is as far as we can go.
If we now “round up” our prime factors of 240 we are left with the following expression:
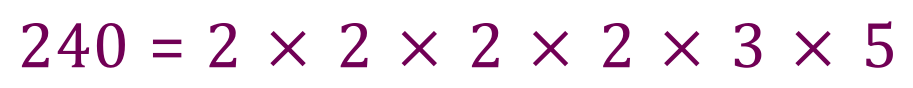
So if we substitute our numbers into the rule:
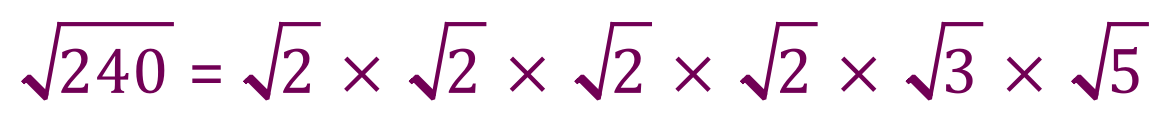
This becomes:
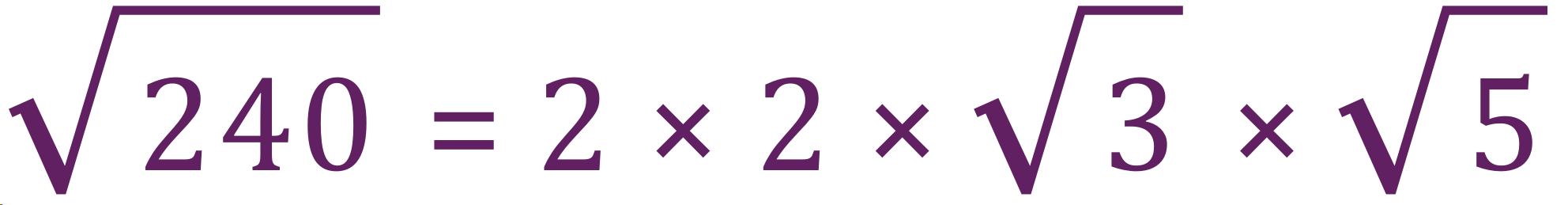
But we don’t leave multiple ‘roots’ in the final answer because it would be more confusing than it was to start with, we simply use the rule of surds to combine the last two roots:
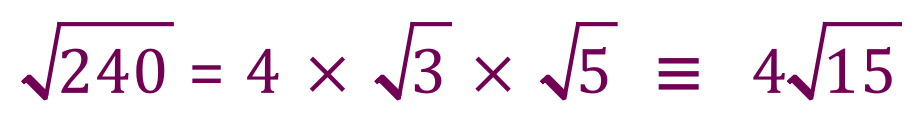
The multiplication signs are not shown normally.
It is important that you understand how these results are achieved, generally speaking we will use a “surd tree” or “prime factors tree” to pictorially represent our simplified results:

there are two ways of looking at this, you could consider this to be the number 88 and therefore a way of finding the prime factors, which in this case would be 2×2×2×11 or if we consider that 88 is in fact “square root 88” then the numbers 2, 2, 2 and 11 would also appear in square root form and therefore the answer to the problem would be (in text format anyway) this:
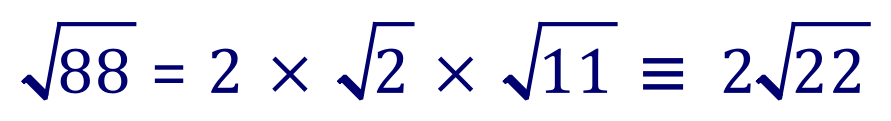
But of course we can’t leave it like this so we look for ways of pairing up, or tidying up the number of smaller surds on the right-hand side of the equation as shown.
Let us take a look at another example:
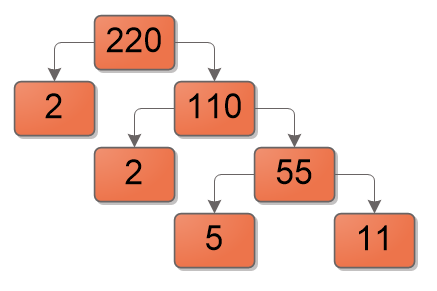
This is slightly more complicated, but we followed the same path. The prime factors of 22 are 2, 2, 5 and 11 but when we consider the surds we follow the usual format and consider them all to be “smaller surds” if such an expression exists (if it didn’t, it does now):
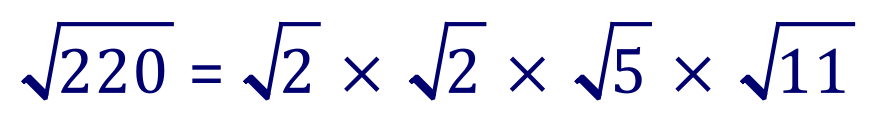
Once again we can “pair up” TWO of our “smaller surds but we are then left with “Root 5” and “Root 11” which can’t be paired, and neither can they be just left as they are so, once again, according to the rules of surds they are multiplied together in our final expression:
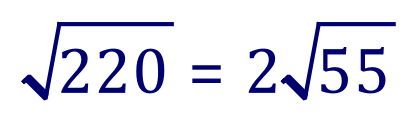
In the last few pages you’ve heard me talk about the “rules of surds” but what exactly are they ?. The rules of surds are simply a set of mathematical operations that can be performed on surds to simplify them.
Go To >> Surds In Trigonometry <<
Go To >> HCM and LCF <<