Surds in Trigonometry
In trigonometry we will encounter a lot of results which have to be quoted to ‘a certain number of decimal places’ but any ‘clipping’ of a result, especially if the result is an irrational number or infinitely repeating decimal (such as 2/9 which is 0.222 infinitely).
For example:
Q. The square root of 2 is 1.414 – Yes or No?
A. BOTH, depending on the level of accuracy you require.
The square root of 2 is 1.4142135623730950488016887242097 to the accuracy of my Windows Calculator but even here it is truncated.
You may be asked to ‘Find ‘x’’ and leave the answer in SURD form, this is a representation of the value for ‘x’ where it involves a square root:
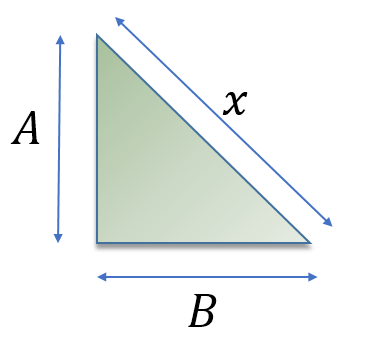
Let A = 1 and B = 1, this is a ‘right isosceles triangle’, what is the value of ‘x’?
Using the formula:
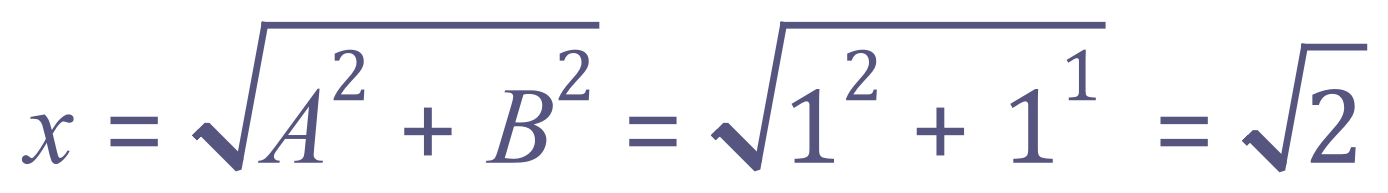
This is the result, you have not been asked to quote an answer to any set number of decimal places, but to leave the answer in SURD form…….the value of ‘x’ is EXACT in this case.
If your answer ends up as the square root of a larger number such as:
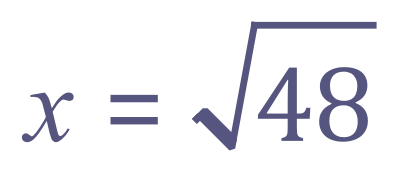
You would be advised to ‘cancel down using prime factors’ to quote your answer:
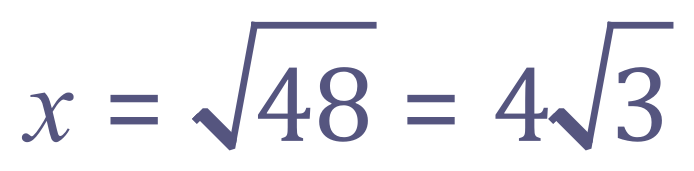
How to do this will follow in another section.
OK let’s throw some numbers into the mix and see what we end up with:
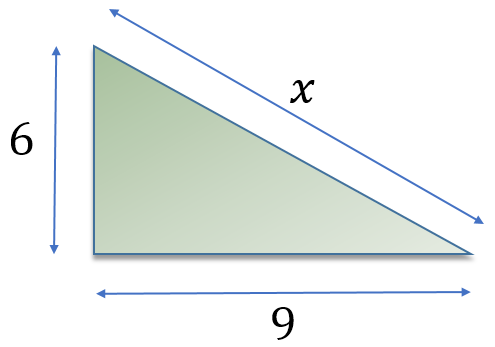
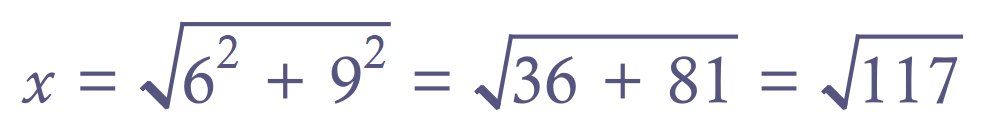
This could be the result, but remember prime factorisation:

ALWAYS remember to quote your answer at the end.
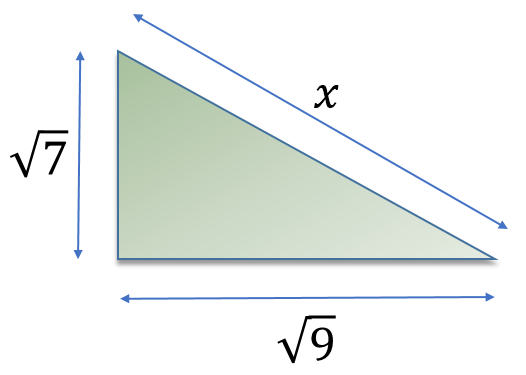
If the examiner is being particularly mean, you might get a question like this:
Doubtful but possible, but remember just do the same thing that you have done before:
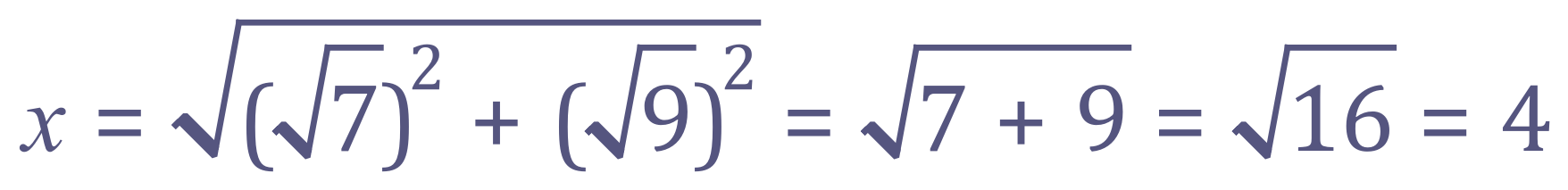
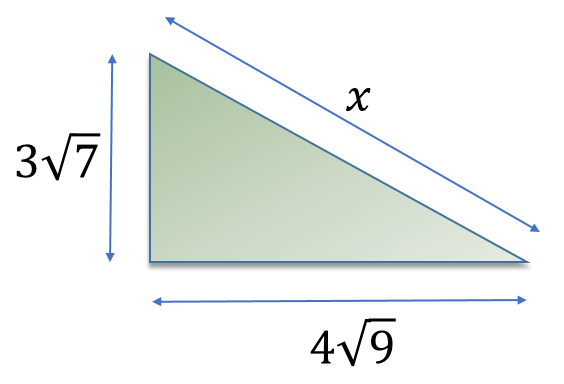
The exam board would be quite sadistic to throw this at you, having said that now that calculators are used in exams it has ‘sped things up’ significantly so why not?
Again, work it out logically:
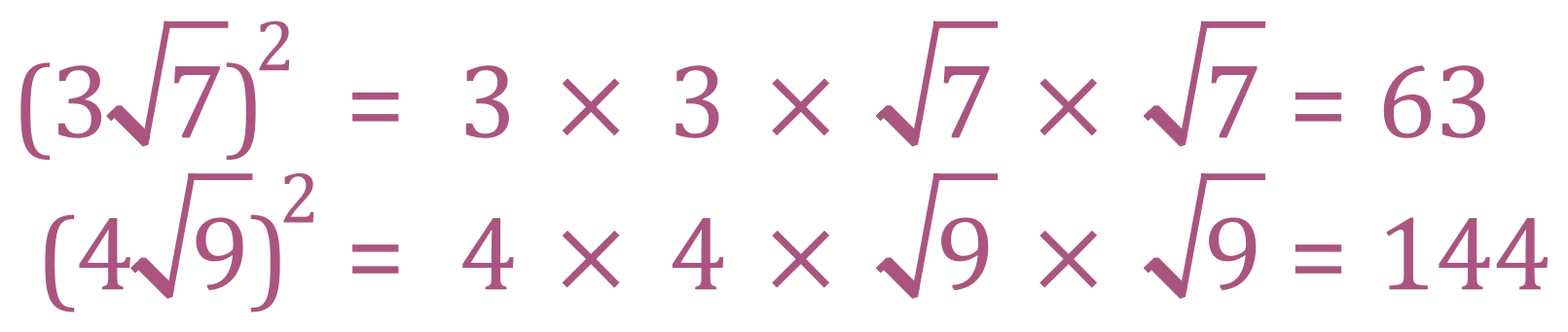
63+144 = 207, so ‘x’ is going to be the square root of 207

We will leave SURDS just for a moment (but not entirely, they creep in everywhere!), but there is one more set of identities that we have to introduce, ones which are fundamental to trigonometry and which are born from the right angles triangle.
Go To >> Surds <<