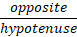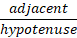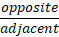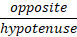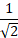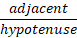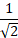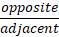Worked Examples in Science and Mathematics

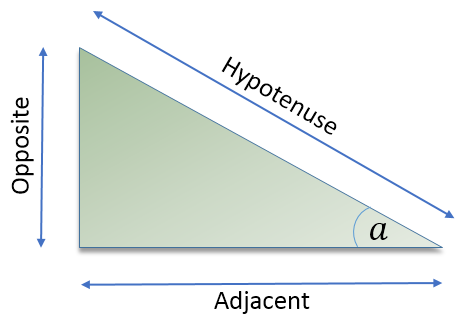
SOHCAHTOA

These identities are defined as ratios of the sides shown in the table, so for example considering the angle ‘a’ the Sine of that angle is the ratio of the opposite side to the hypotenuse and the cosine / tangent are the relevant ratios as per the table.

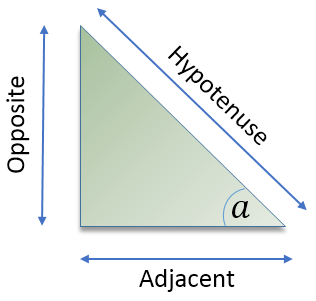
Consider the angle a = 450

This would make the triangle a ‘right isosceles triangle’ so that the complementary angle (at the top of the diagram) is also 450. The opposite and adjacent sides are equal, let us say that they are Opposite = 1 and Adjacent = 1.

Pythagoras would say that the length of the Hypotenuse is 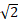so according to our SIN / COS / TAN table we have:  

In general maths you will possibly use the values in further calculations, otherwise the SURD form may be all that you need.

Now I am going to look at two other types of right angled triangle referred to in trigonometry, the 3-4-5 triangle and the 30-60-90 triangle. These will lead us to some more standard SURDS.

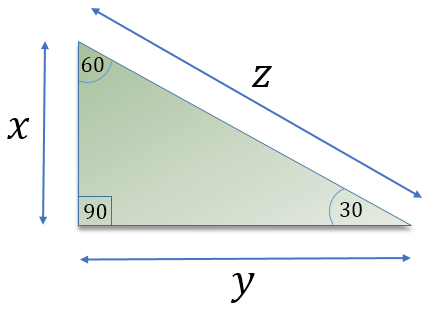
In this case we have all of the angles, but as we have none of the sides we can’t work them out.

Let us state that x = 1 so that the sine of the 300 angle is defined as:

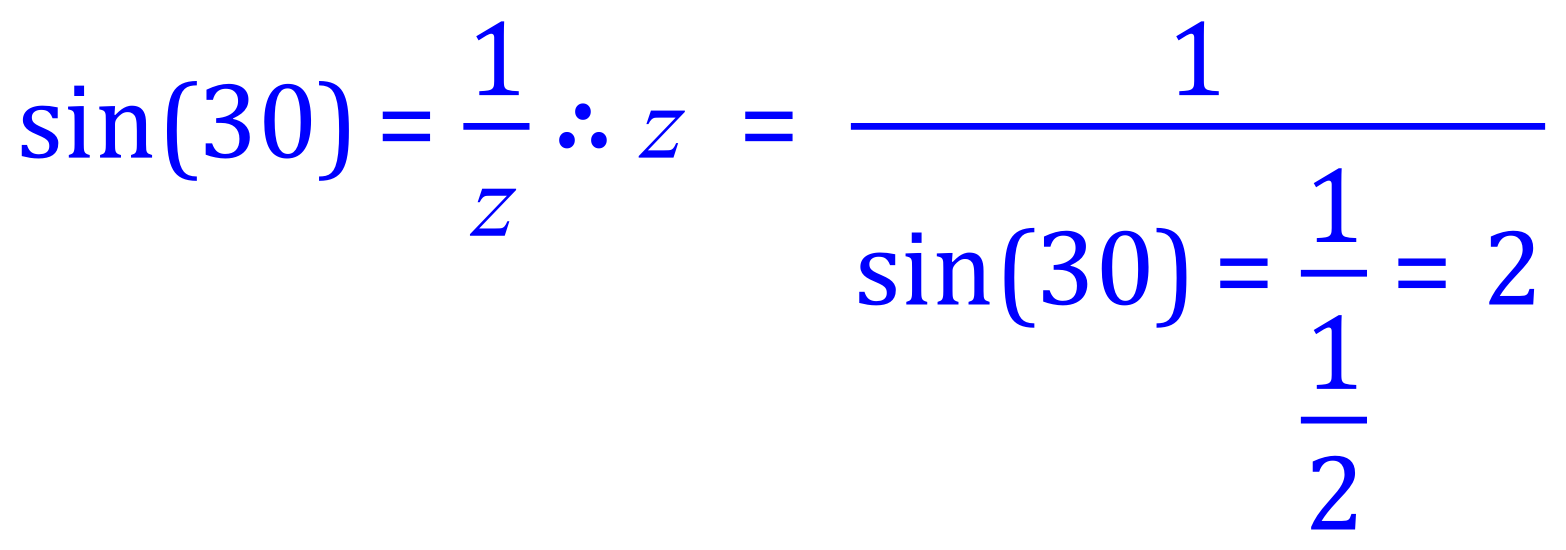
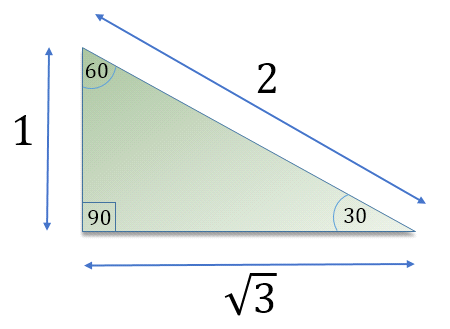
We can now use Pythagoras Theorem to evaluate ‘y’

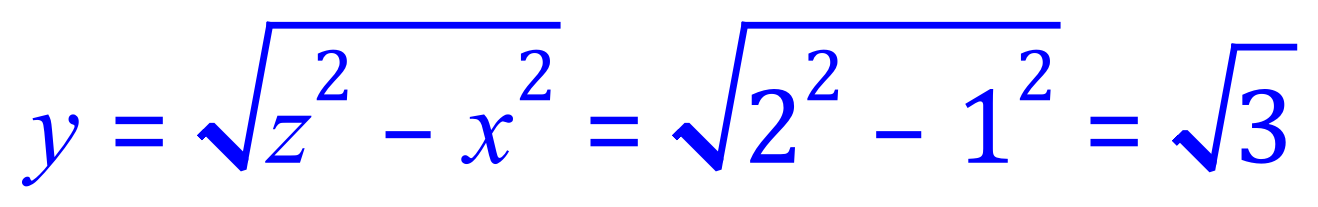
So now we can say that in a 30-60-90 triangle the sides are in the proportion of:

Now let’s look at the 3-4-5 triangle.

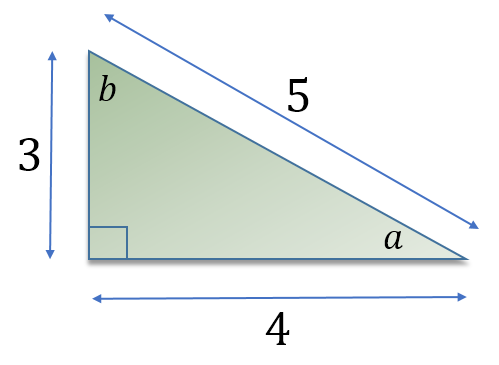
The triangle above is one of the ‘Pythagorean Triples’, in that if the sides above are multiplied by the same integer value, i.e.: remaining in proportion the resulting triangle will also be a ‘triple’:

“A ‘Pythagorean Triple’ is a right angled triangle with sides in such ratio that the Pythagoras Theorem is satisfied”

The 3-4-5 triangle is the simplest one (because 32 + 42 = 52) but there are infinitely more, for example just multiplying the sides here by 2 making it a 6-8-10 still satisfies the theorem (since 62 + 82 = 102).

Note though that the angles ‘a’ and ‘b’ are NOT 300 and 600 respectively even though you might think that they are, in fact we can use the SIN COS TAN identities to work them out:

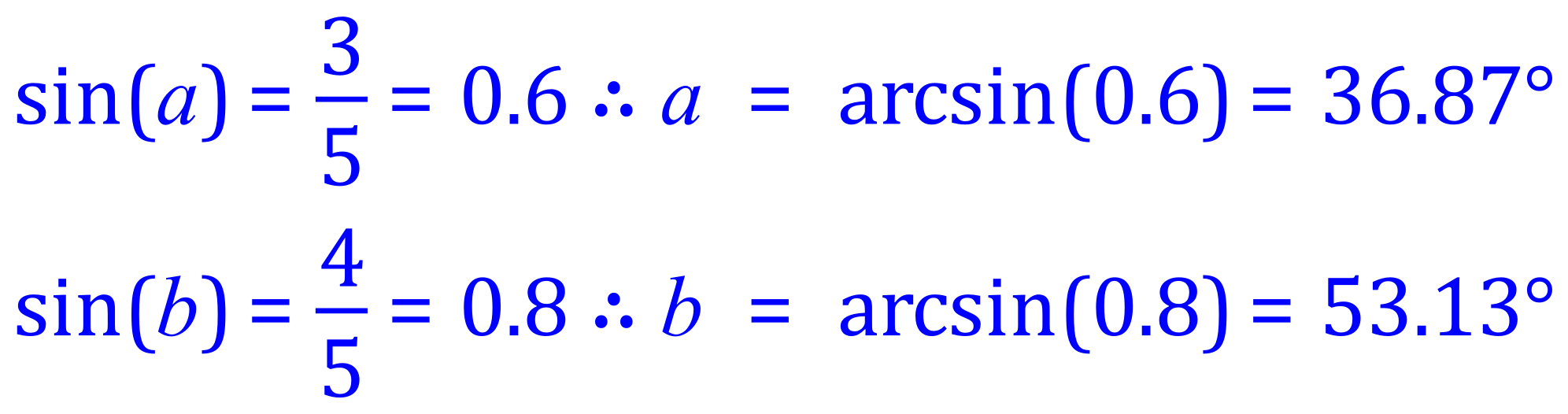
Arcsine is the ‘undoing’ or ‘reversing’ of the sin operation, if you have, for example, the sin of an angle 'x' eg: sin (x) you can find ‘x’ by taking the arcsine, sometimes referred to as sin-1  :

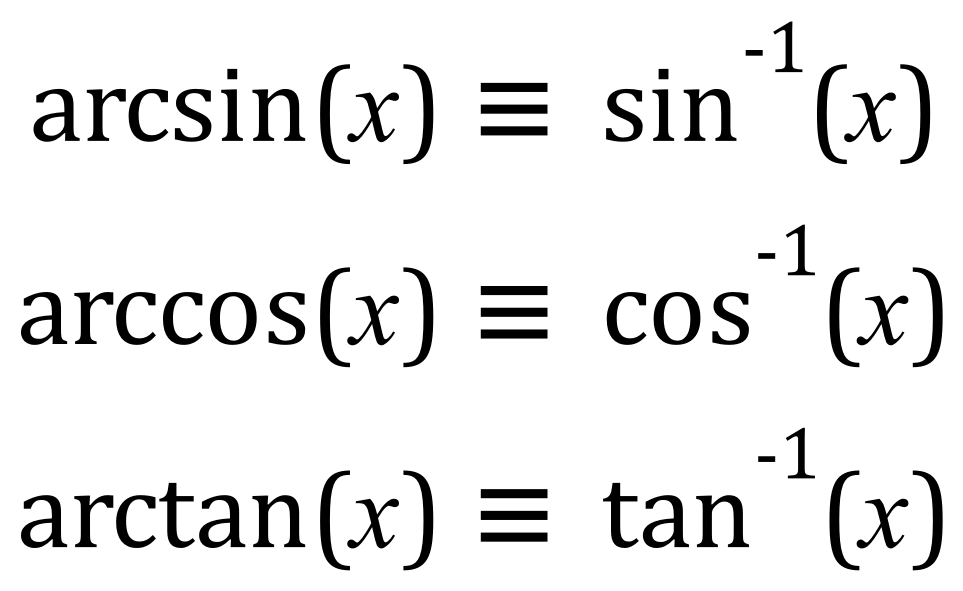
Note that these angles are complementary, adding up to 900 and along with the right angle they satisfy the rule for the sum of the internal angles of a triangle.

>> Table of Trigonometric Ratios <<