Higher Order Equations
This is where it can get messy, as you know the formula for solving the quadratic is:
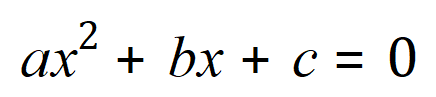
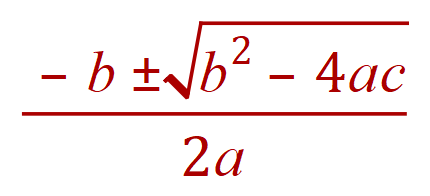
There is a ‘similar’ formula for the solution to a cubic equation, that is, an equation with an ‘x3’ term having three roots…….
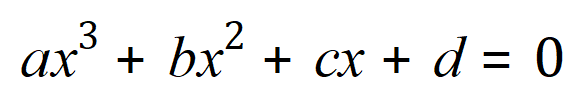

You shouldn’t be too surprised to find that I don’t intend to go any further with this formula, suffice it to say that if I entered:
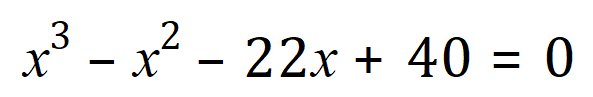
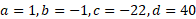
As my source equation I would (hopefully) come back with roots of ‘x’ = +4, +2 and -5. Quite obviously the graphical solution is better but it would only be an approximation in many cases:
Quartics and Beyond
To close this session I will now talk briefly about equations with higher powers of ‘x’

The picture above shows a quadratic, a cubic, a quartic and so on right up to the power of 10 for the ‘xn’ term.
I have, in fact, created at this table by taking the roots of a known quadratic equation (the one at the top) and by throwing at the end of it a ‘random root’ and multiplying out (in algebraic speak ‘expanding’) I have arrived at the next order equation. (I did this manually (pen and paper) up to x7 but as you can see it gets quite big!).
Here is the plot for the OCTIC (x to the power of 8) equation:
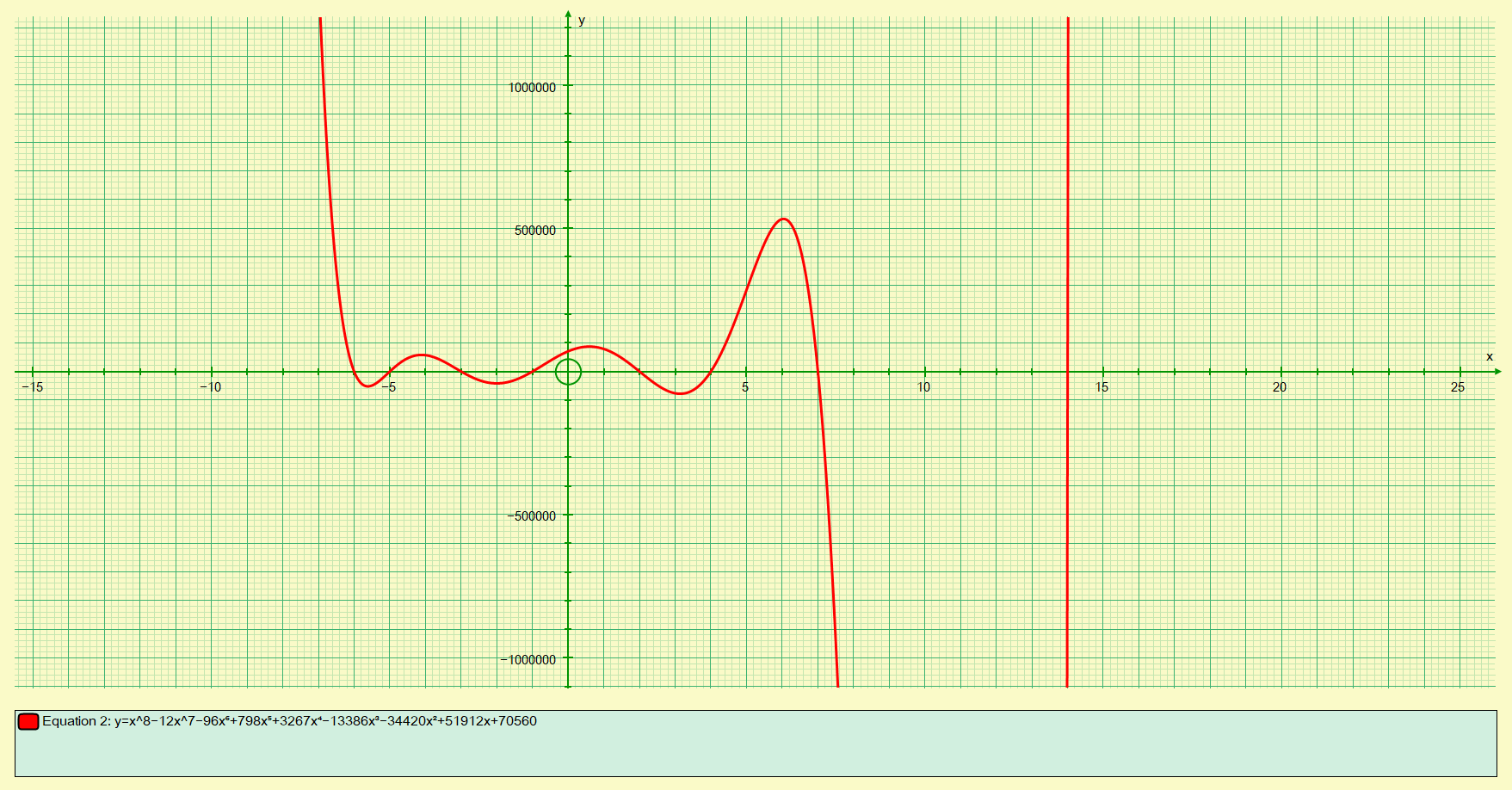
This plot shows the 8 roots of the equation, but it is pushing the software that created it quite hard.