(Gravitational) Potential Energy
Q1. A weightlifter in a gymnasium raises a dumbbell of mass 16 kg through a height of 2 m from the ground to just above his head. How much gravitational potential energy has the dumbbell gained? Take the gravitational field strength to be in 9.81 N per kilogram.
A. As is often the case, the first questions you are likely to encounter will be straightforward "substitute values" directly into the equation, this question is a simple example of that. Looking at the information we have got, we have a value for the mass (16 kg) value for the gravitational field strength (9.81 N per kilogram) and a height of 2 m. "Plugging" these values into the equation gives the following result:
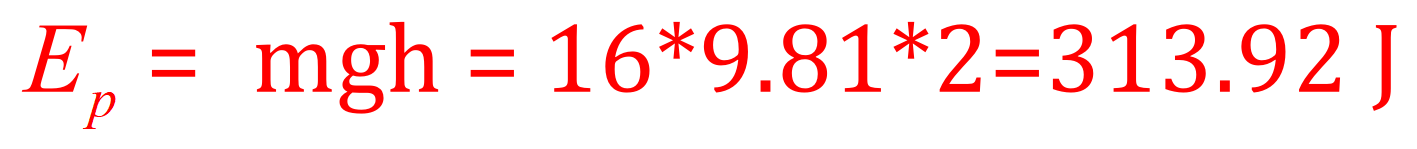
Q2. An engineer takes his box of tools from the back of his van in the car park of a tower block to the roof space at the top in order to carry out some repair work. The engineers toolbox has a mass of 35 kg. Taking the gravitational field strength as 9.81 N per kilogram, approximately how tall is the tower block given that the toolbox holds 60,086.25 J of energy in its gravitational potential energy store when the engineer reaches the roof, and taking the gravitational field strength to be 9.81 N per kilogram?
A. Not unsurprisingly, this question is a little bit more demanding and requires you to transpose the equation in terms of your unknown variable. Taking a look at what we do know, we know the value of the gravitational potential energy (60,086.25 J) and we also know the gravitational field strength which is 9.81 N per kilogram. What we don't know is the height, and this is what the question asks us to find out.
Using the equation:
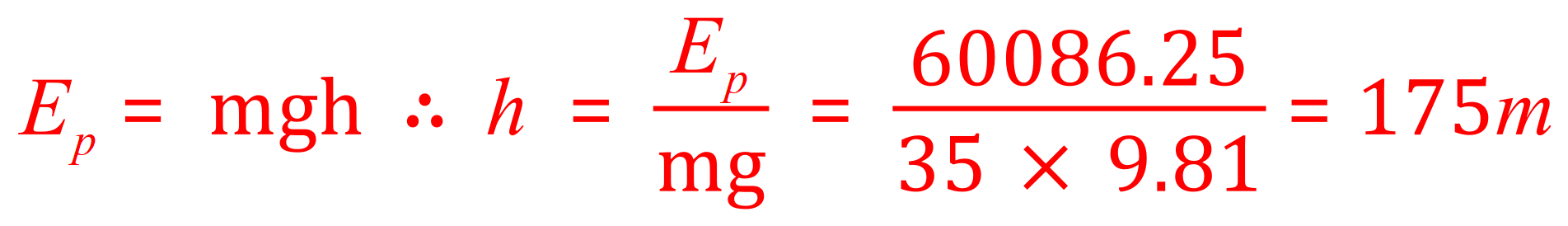
Q3. The engineer in the previous question is quite reckless, and during his repairs at the top of the block of flats he accidentally drops a large spanner of mass 800 g from his work area and it falls to the ground. Given the gravitational field strength of 9.81 N per kilogram, at what speed do you think the spanner would hit the ground?
A. Understandably, your first reaction to this sort of question might be "Huh??" As it's not the sort of thing you've seen before. Take into account what you already established, or what you already know about kinetic energy, gravitational potential energy and the law of conservation of energy and you should be able to work out what the question is asking.Let us look into this a little bit more. From the previous question we established that the engineer was working at a height of 175 m, we are given the gravitational field strength as 9.81 N per kilogram and we are told that the mass of the spanner is 800 g. What can we establish at this point with this information?
Well we have a value for "m", a value for "g" and a value for "h". Looking back at the equations we've learned so far you can see that these three properties are just what we need to calculate gravitational potential energy. Bearing in mind that the mass of the spanner is given in grams, 800 g and we will need to 1st of all convert this into the units that the equation expects, we convert 800 g which will become 0.8 kg.

So, we now know that while our spanner is sitting quite happily on the ledge it possesses 1373.4 J of gravitational potential energy. But, unfortunately our spanner is knocked over the edge and falls to the ground at a velocity which we have been asked to calculate. What is happening to the spanner as it falls?
Energy is being transferred from the spanners gravitational potential energy store to the spanners kinetic energy store. Assuming that we have no relevant energy dissipation by a friction / air resistance or anything like that as the spanner falls (that could just complicate what is intended to be a fairly straightforward question) we know from the law of conservation of energy that all of the gravitational potential energy must be converted to kinetic energy as the spanner falls.
Therefore, at an instant before the spanner hits the ground, it will have 1373.4 J of energy in its kinetic energy store. As it is infinitesimally high off the ground we can say that "h" is zero therefore the gravitational potential energy will also be zero (think about it, if E=mgh and H is zero, then E must also be zero?).
How can we therefore establish the velocity? Well, think about it, we have a value for the kinetic energy, we have a value for "m" of 0.8 kg, the only thing we are missing is the velocity.
Can you think of any equation you may have come across so far where these values could be used?
Look at the equation for kinetic energy:
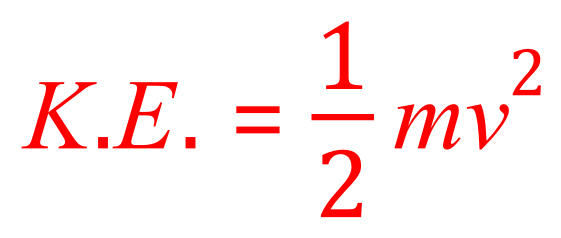
We have values for all of the variables with the exception of "v", so if we transpose equation in terms of the (which we have done previously) will be able to answer the question posed:
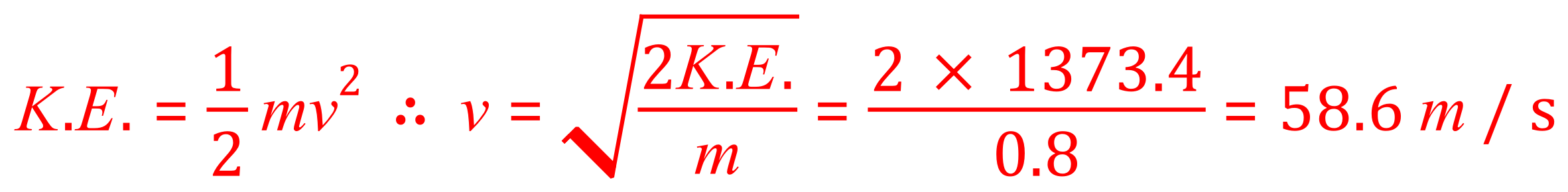
This is quite a considerable speed (131 mph) and a metal object of that mass, travelling at that speed would almost certainly kill anyone if it hit them.
Q4. A driver for the local parcel delivery service has a mass of 110 kg. Carrying a 15 kg box he walks up six flights of stairs to the sixth floor of a tower block approximately 60 m. Calculate the change in gravitational potential energy of the box assuming that it is carried at a height of 1 m from the ground.
A. We are given the mass of the box is 10 kg, the gravitational field strength is 9.81 N per kilogram and the box is starting off at 1 m from the ground. Therefore its gravitational potential energy at this point is simply the product of mass multiplied by gravitational field strength multiplied by the height of 1 m or 10×9.81×1 = 98.1 Joules. At the end of the journey, the box will have travelled through a vertical height of 60m assuming that it is still 1 m from the ground (that is the floor that the delivery man is now standing on) but overall the box will have travelled through a vertical height of 60 m but will now be 61 m from the ground).
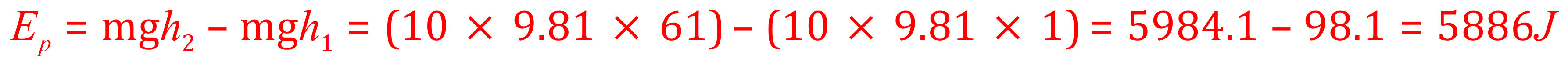
In this particular case it would have been just as easy to put 60 m for the height but I wanted you to see that this was asking for a difference, a change in the gravitational potential energy not a statement of what it was at the end of the journey. The reason I did this is because any object above 0 m will have some gravitational potential energy. This object had a certain amount at 1 m and a larger amount at 61 m, the difference being what the question asked you to calculate.
Q5. A 25,000 kg space vehicle takes off from a planet and climbs to a height of 12,000 m ready to dock with the mother ship. At the 12,000 m point the space vehicle has 2 940 000 000 J of energy in its gravitational potential energy store.Calculate the gravitational field strength in newtons per kilogram of the planet.
A. Sometimes, questions can be wrapped in a convincing scenario such as this one about space travel and leaving the surface of an alien planet that this can cleverly shroud what is essentially a fairly straightforward question. We have values for the gravitational potential energy, the mass and height so it is simply a case of transposing the equation for gravitational potential energy in terms of 'g':

Remember that in questions like this there is plenty of scope for values to be given to you in standard form, for example the energy of the spaceship could be given to you as 2940 MJ which you would have to convert into Joules before you used it. Similarly the height could have been stated as 12 km, and the mass of the spaceship could have been given as 25T (metric tonnes). All of these values would have had to be converted before they could be used.
Q6. An astronaut, stands on the edge of a 455-metre cliff situated at the edge of a crater on Mars. Given that the mass of the astronaut plus all of his equipment is 110 kg, what is the value of the acceleration due to gravity on Mars if his GPE is 185185J?
A. This question requires you to transpose the formula for gravitational potential energy, making "g" the subject:
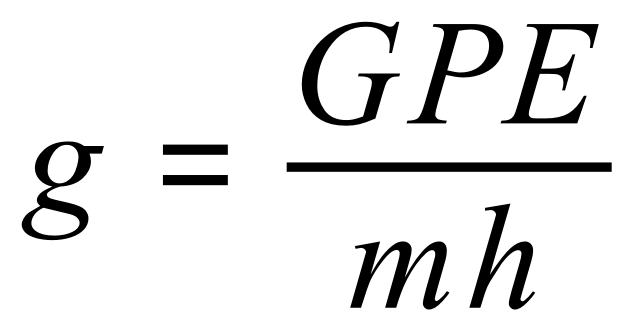
Now plug in the data you have been given:
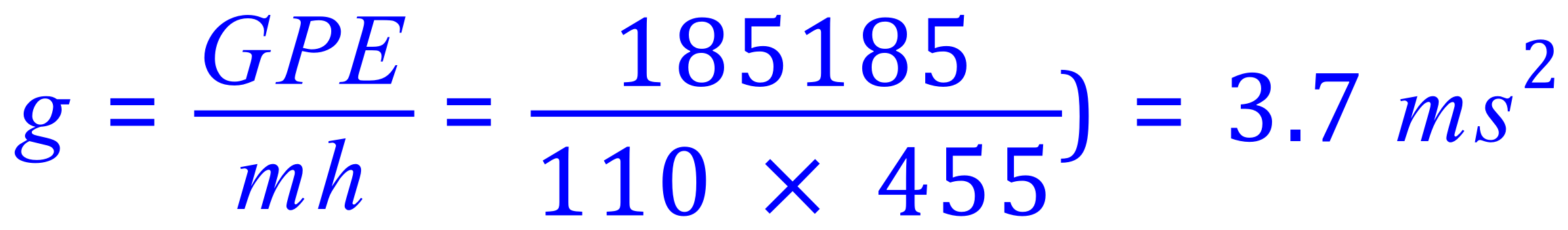
Q7. A small test rocket with a mass of 250 kg blasts off from a launchpad. At a height of 300 m a parachute is deployed and the rocket returns safely to earth. What is the gravitational potential energy of the rocket at its highest point just before the parachute is deployed? Take the acceleration due to gravity as 9.81 m/s/s.
A. Once again, another typical "plug and play" type of question. We are given all of the values we need, and they are already in the correct units so we can literally just insert them into the equation:
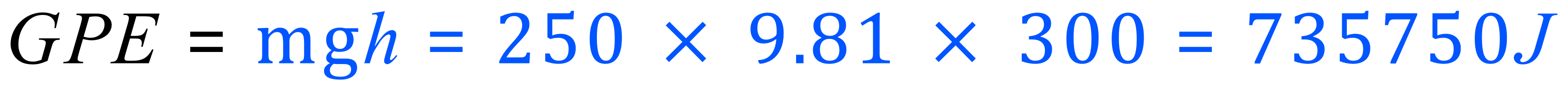
Q8. A space exploration lands on a distant planet with a gravity similar to that of Jupiter. A 50Kg boulder stands at the top of a sheer drop into a crater. Scientific instrumentation detects the boulder falling and crashing at the base of the crater, hitting the ground at 175 m/s. Taking the acceleration due to gravity on this planet as 26.49 m/s/s calculate the height of the drop into the crater.
A. The law of conservation of energy is a physical law that states energy cannot be created or destroyed but may be changed from one form to another. There is nothing in the question to say that energy is "lost" through air resistance (friction) or sound energy when the object crashes, so we assume rightly that the KE of the body at the point of impact is the same as the GPE at the beginning, before the fall.
In this case GPE (start) = PE (end), so we calculate the KE that the boulder had, given its mass and velocity of impact:
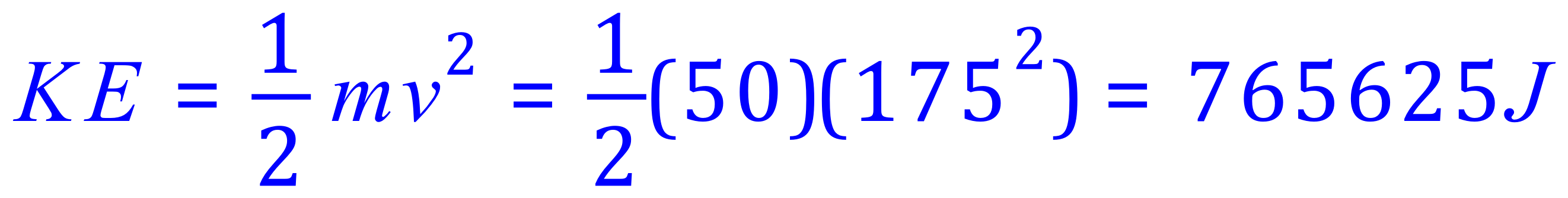
By the LOCOE above, this would also be the value of the GPE at the start of the fall:
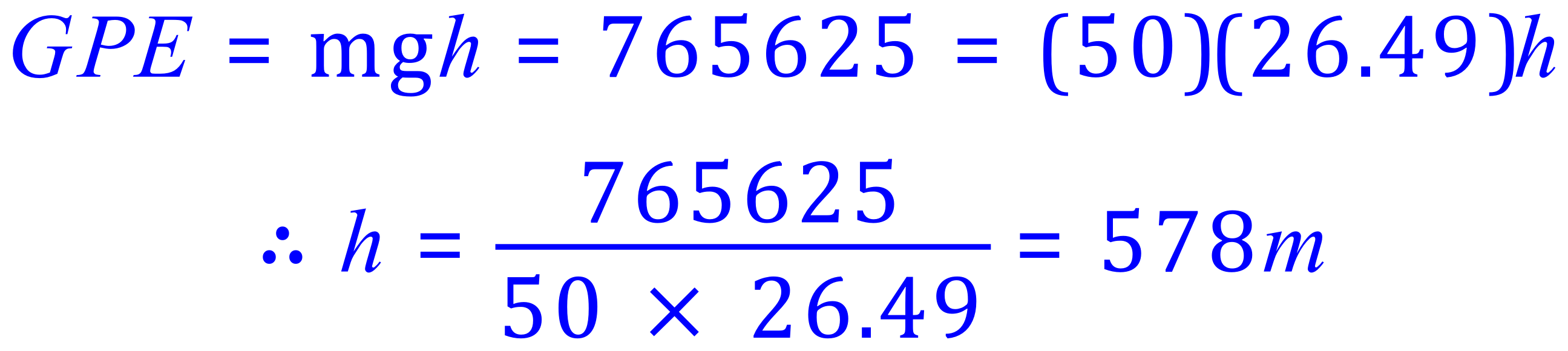
Incidentally, the boulder hits the ground at 175 m/s which is about 392 mph !!
Back To >> Questions <<
Back To >> Gravitational Potential Energy <<