Momentum
Q1. A 60 Kg boulder falls from the edge of a cliff, reaching a speed of 14 metres per second. Calculate the boulder's momentum.
A1. Quite a simple question to start with, this is simply an insertion of given data into the equation for momentum:

Q2. A 12g bullet is shot from a rifle, and has a momentum of 10.728 Kg m/s. What is its muzzle velocity, in miles per hour?
A2. Lots of conversions to do here. First of all let us convert mass to Kg. 12g = 0.012 Kg, velocity is the required value and momentum 'p' is given as 10.728 Kg m/s:
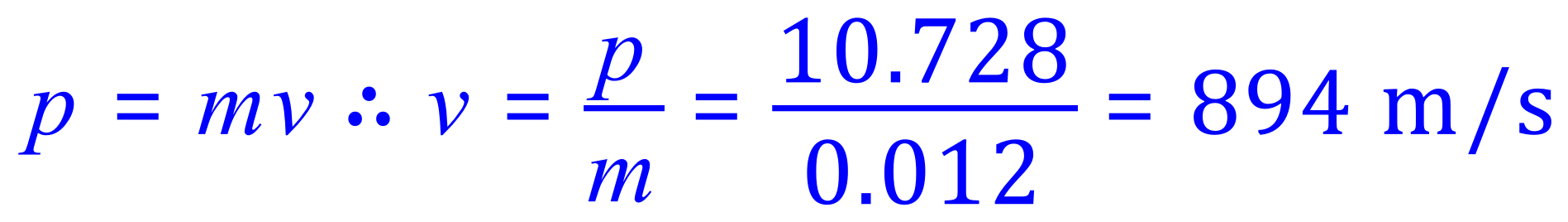
There are 1609.35 metres in one mile, therefore this bullet travels at:
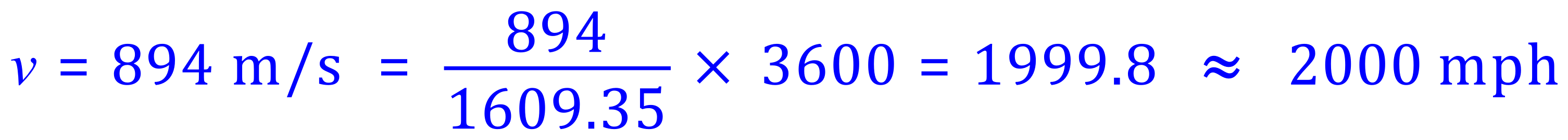
Q3. A car with a mass of 1000 kg is travelling at a velocity of 20 m/s when it collides with a stationary car of the same mass. After the impact both vehicles move off together, calculate their velocity.
A3.
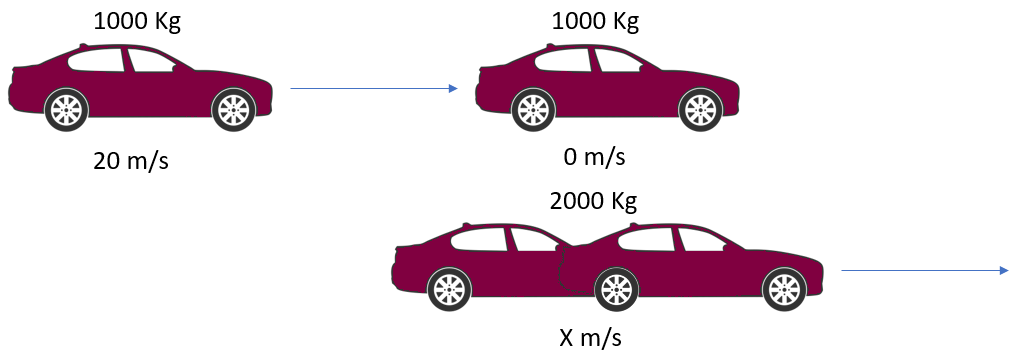
The law of conservation of momentum tell us that the total momentum before the impact must equal the total momentum after the impact. In the case of "before" the total momentum is 20,000 kg metres per second as the second vehicle is stationary and therefore has no momentum.
In the second case "after" the impact, the combined mass is now 2000 kg and the velocity with which the vehicles are moving forward we will call V2 (X in the picture).
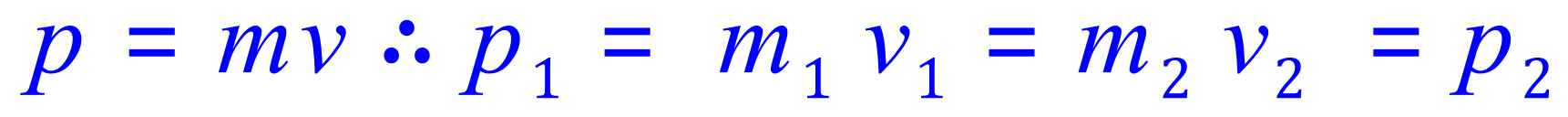
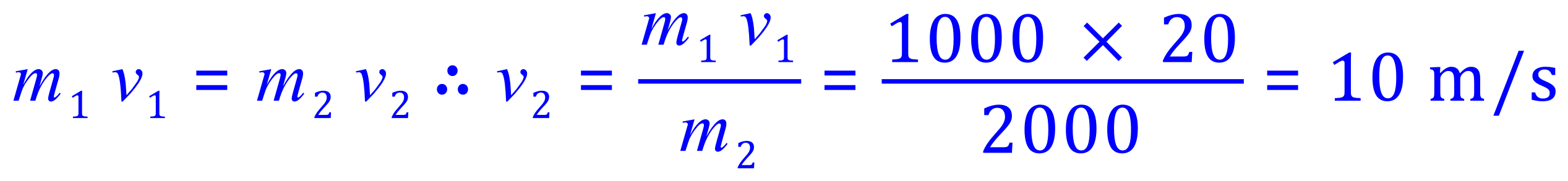
Q4. A lorry of mass 12,000 kg travelling along at a velocity of 15 m/s, crashes into the back of a moving car with a mass of 1500 kg, travelling at a velocity of 5 m/s. Upon collision, the vehicles remain in contact. Calculate their forward velocity.
A4.
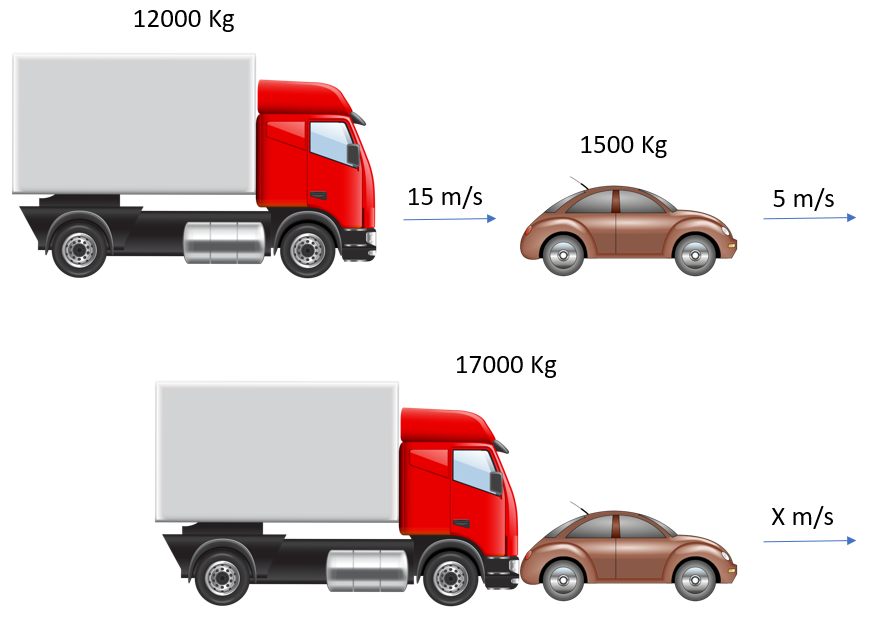
This is the same sort of question as the previous one, the law of conservation of momentum states that the momentum before the collision (that is the total momentum of both vehicles) must equal the total momentum after the collision. The point to remember here is the combined mass of the two objects needs to be taken into consideration when performing the calculation:
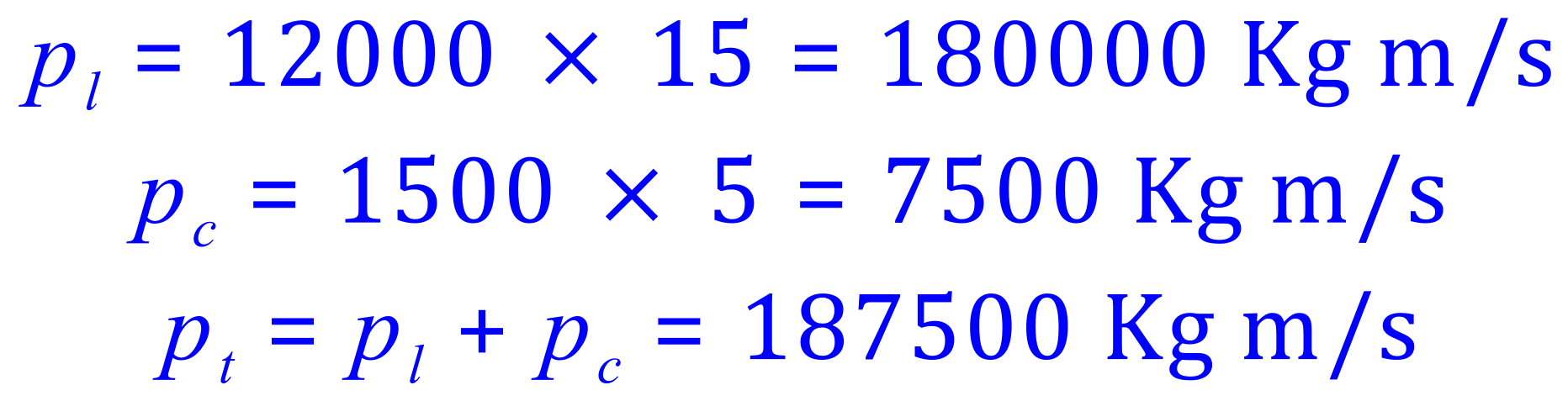
This figure represents the total momentum of the combined lorry and vehicle. The combined mass is easy to see, therefore all we need to do now is to rearrange the standard equation for momentum in terms of velocity to get the new velocity for the combined masses:
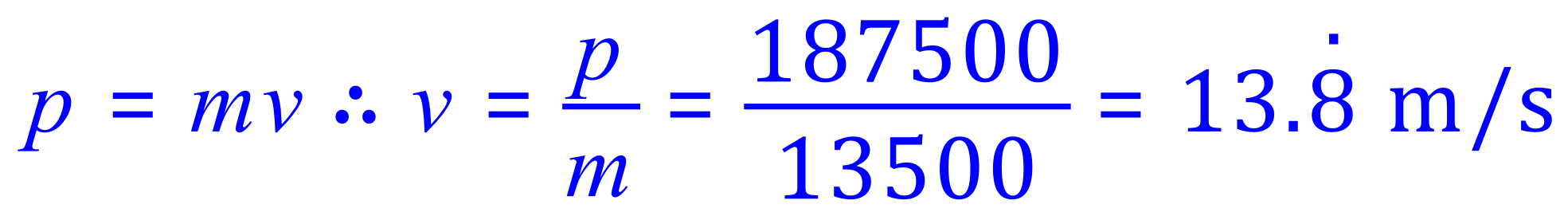
Q5. A rifle with a mass 3 kg fires a bullet with a mass of 100 g at a velocity of 250 m/s. What is the recoil velocity of the gun?
A5.The key here is to make sure that all of your units are converted into the standard units. When we talk about momentum, we talk about (usually) kilogram metres per second, so we need to convert our bullet into kilograms. 100 g is 0.1 kg.

As well as being a question on momentum, this is a good example of Newton's third law. The momentum of the bullet is quite easy to calculate, you can probably see that it is 25 kg metres per second, and as it is travelling to the right will say that this is in the "positive" direction. The garden will recoil in the "negative" direction with an equal momentum of 25 kg metres per second (Newton's 3rd Law). We know the mass of the gun, we need to know calculate the recoil velocity.
The momentum before and after the "events" will be the same, it will be zero. If you think about it, before the rifle is fired, there is NO momentum, therefore there can be NO momentum afterwards.
V1 is positive, V2 is negative as it is in the opposite direction:
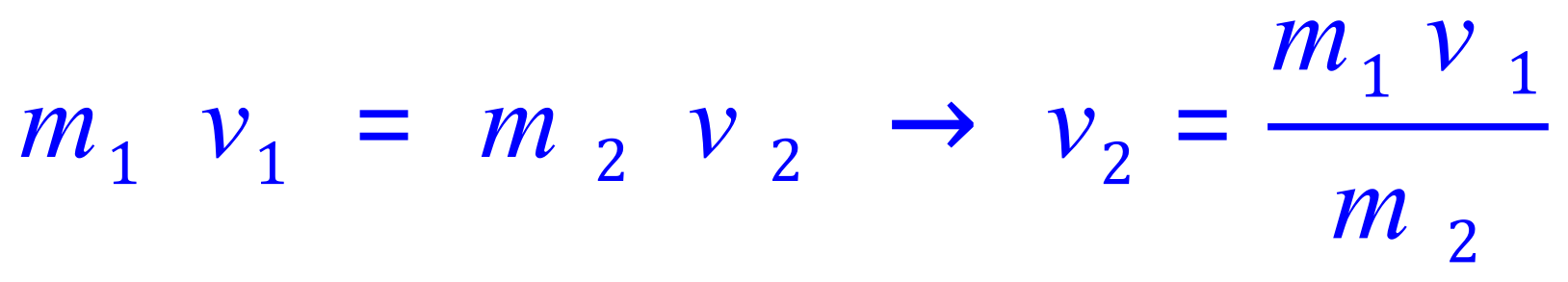
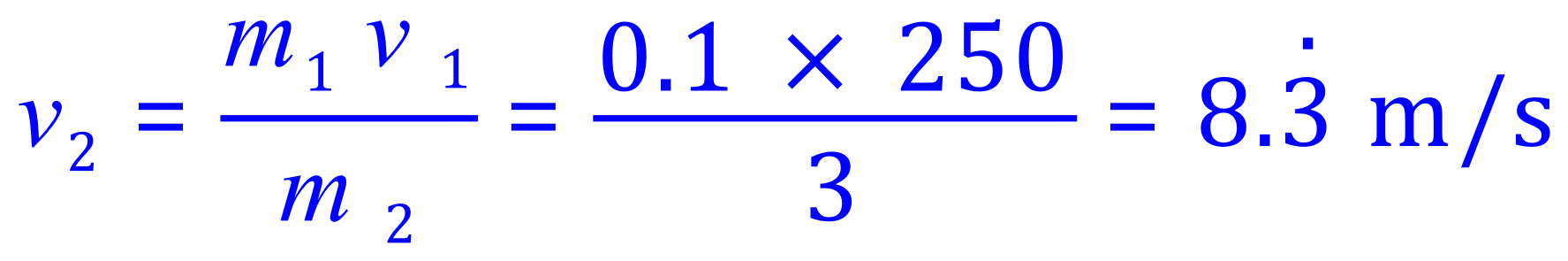
You would state the answer as MINUS 8.3 m/s, or 8.3 m/s to the left, or 8.3 m/s in the opposite direction showing the conservation of momentum.
Q6. A standard bowling ball, of mass 5 Kg is bowled along a tenpin bowling run/track. Assuming no energy losses due to friction, air resistance etc, what will its Kinetic Energy be, in Joules, when it strikes the centre pin with a momentum of 15 Kg m/s ??
A6. A little mix up of physics to make you think. The momentum is given and from this we can establish velocity:
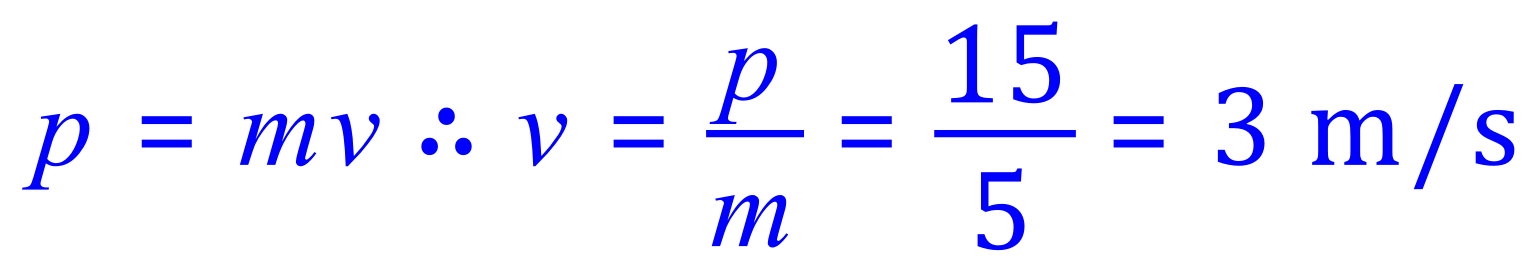
Now that we have the velocity we can calculate the KE, as the mass is already known to be 5 Kg:
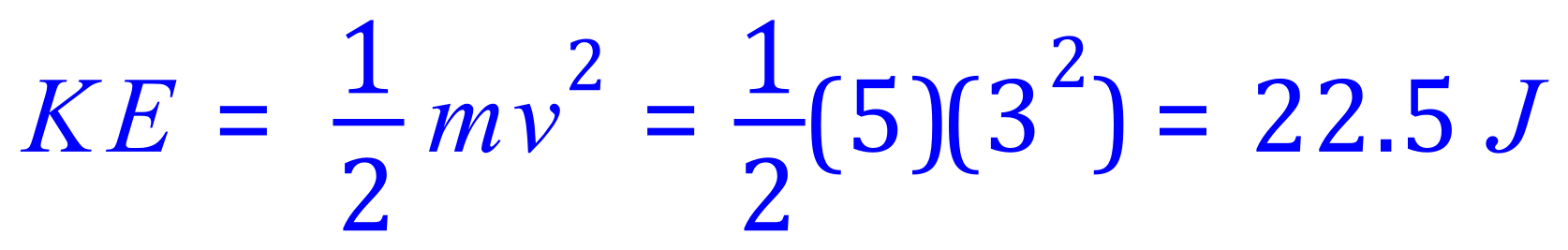
Q7. A cannon fires a cannonball with a mass of 10 kg at a velocity of 100 m/s, this causes the cannon to recoil at 2 m/s. What is the mass of the cannon?
A7. Again this is an example of "momentum before event equals momentum after event" which of course is zero.
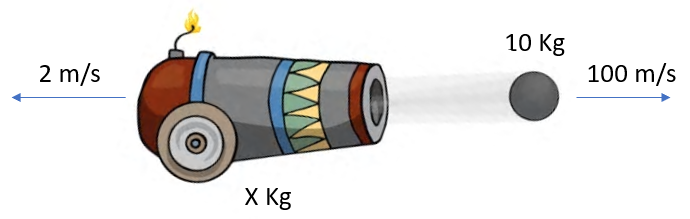
As stated above, the momentum before the cannon is fired is zero, the cannon is not moving and neither is the ball. After firing, the ball has a momentum of 1000 kg metres per second (you should be able to work this out from p=mv). Taking a slightly different approach to the explanation of the second part of the question, the momentum of the cannon must also be 1000 kg metres per second, but in the opposite direction so we could effectively regard this as "negative" because 1000 + (-1000) = 0
As the cannon recoils at 2 m/s, it must have a mass of:
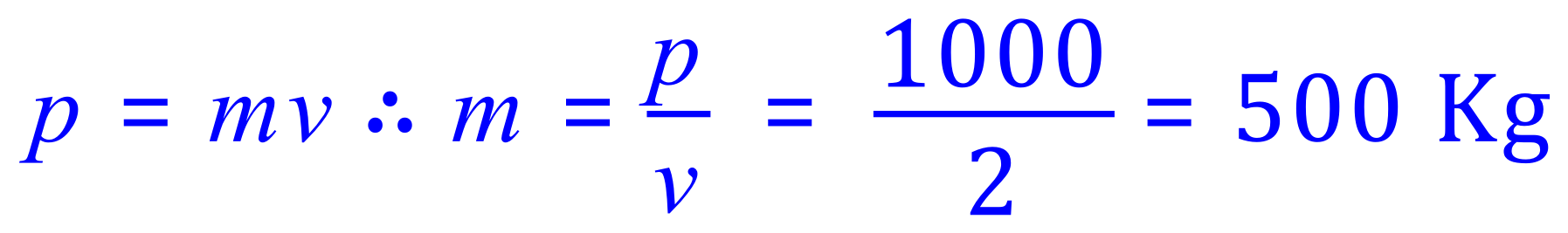
Q8. An astronaut, during an EVA session (extravehicular activity, otherwise known as a "spacewalk") with a mass of 125 Kg throws a 15Kg used equipment pack forwards, in front of him at a velocity of 2.5 m/s. In which direction will the astronaut travel and at what velocity?
A8.This question is no different to any of the others, the momentum before the astronaut throws the pack will be zero, as will the momentum after the pack has been thrown.
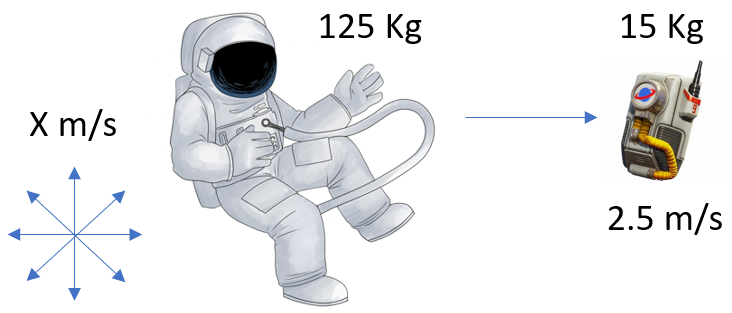
I think you probably know by now that the astronaut will move away from the pack, so that part of the question should be quite obvious. But what will his velocity be?
Remember (Pb = momentum before, Pa = momentum after)
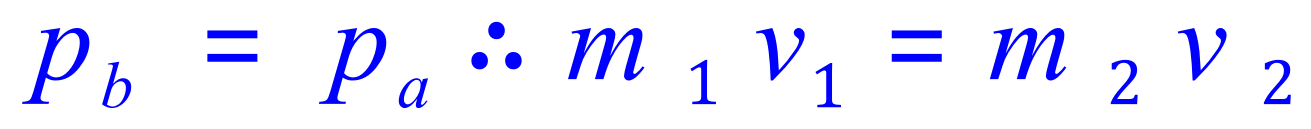
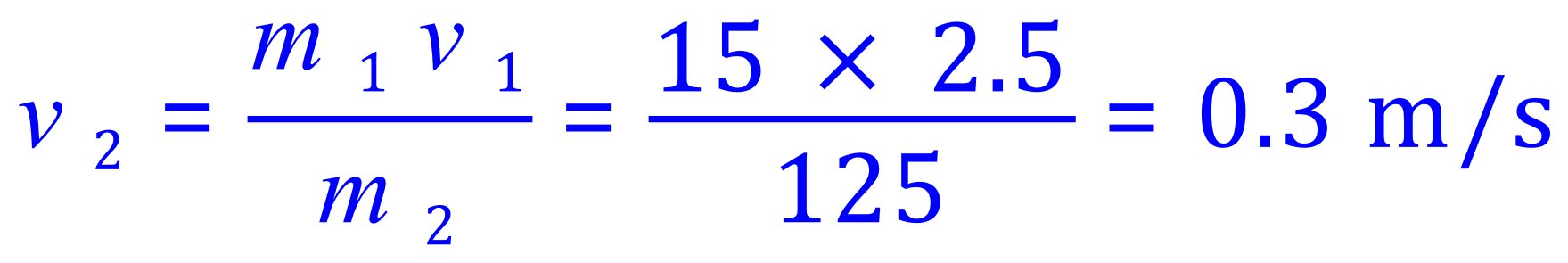
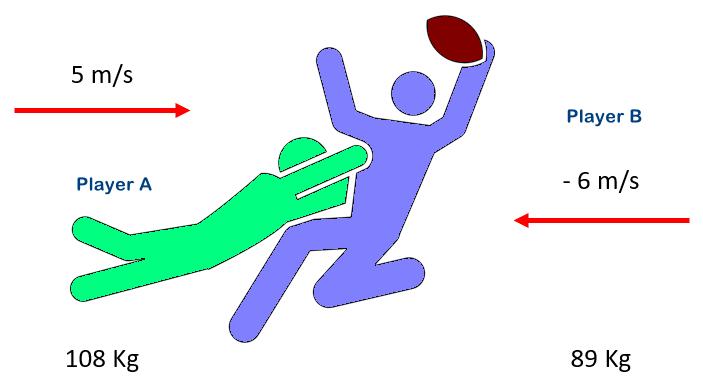
Q9. Two rugby players, Player A and Player B are charging towards each other. They have masses of 108 Kg and 89 Kg respectively. Player A is running towards Player B at 5 m/s and Player B is running towards Player A at 6 m/s. They collide with each other. What will their velocity be after the collision, and in which direction?
A9. Tricky here, the conservation of momentum has to be applied which states that the momentum before and after the collision must be the same. Let us work out some values, and allocate some directions.
Let us state that Player A is running to the right, in a positive direction. At 108 Kg and 5 m/s he will have a momentum of 108 x 5 = 540 Kg m/s
Let us state that Player B is running to the left, in a negative direction. At 89 Kg and - 6 m/s he will have a momentum of 89 x 6 = - 534 Kg m/s
The total momentum is 540 + (-534) = 6 Kg m/s to the right and this represents the new momentum with the newly combined mass of 108+89=197 Kg.
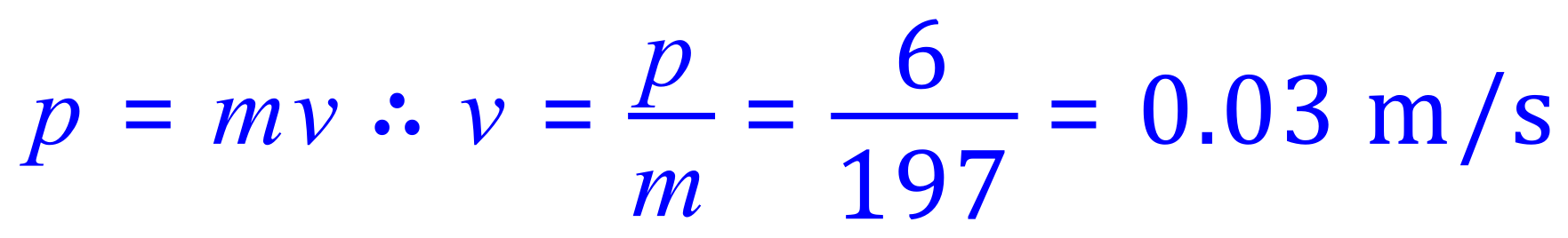
This is still a positive value so they will travel in the direction that Player A was already heading...slowly and painfully 8-)
Q10. Two steel balls approaching from opposite directions collide and move off together to the left at 1.5 m/s. The first ball (moving to the right) has a mass of 5.6Kg and was moving at 1.3 m/s. The second ball has a mass of 7 Kg. What was the approach velocity of the second ball before the collision?
A10. If this is a little hard to visualise, a sketch might help:
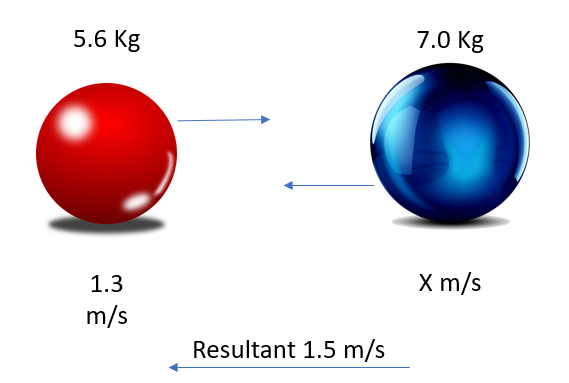
We need to denote a POSITIVE and NEGATIVE direction here, let us say that the RED ball is travelling to the RIGHT in a POSITIVE direction and the BLUE ball is travelling to the LEFT in a NEGATIVE direction.
The momentum of the RED ball is:
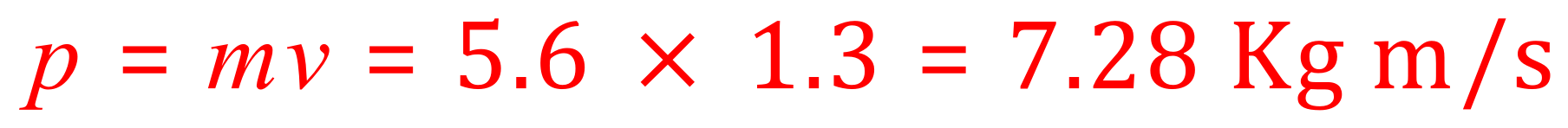
The momentum of the BLUE ball is:
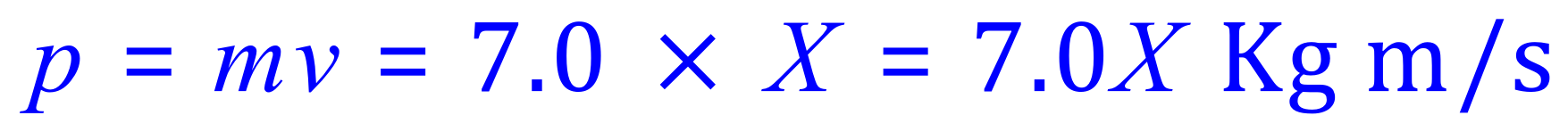
The law of conservation of momentum states that the total momentum BEFORE impact = total momentum AFTER impact. We have a known resultant direction (which we have stated will be NEGATIVE as it is to the LEFT) and velocity of -1.5 m/s, combined mass of 5.6 + 7.0 = 12.6 Kg.
Final momentum:
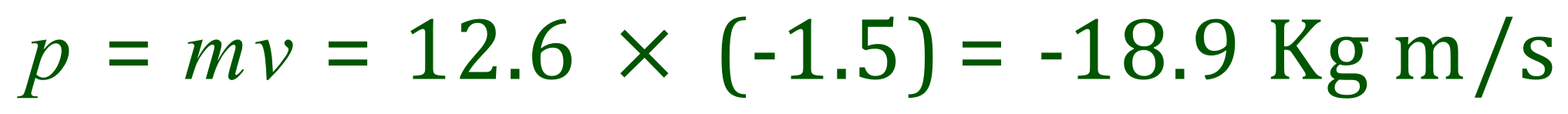
And this is also the sum of the momentum before collision:
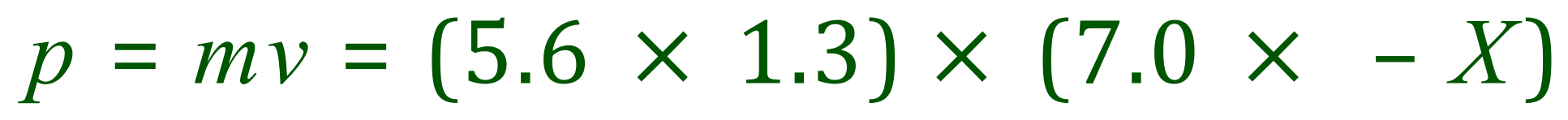
So:
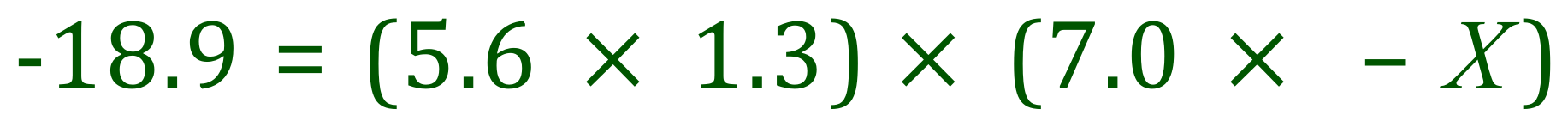
Rearranging for X:
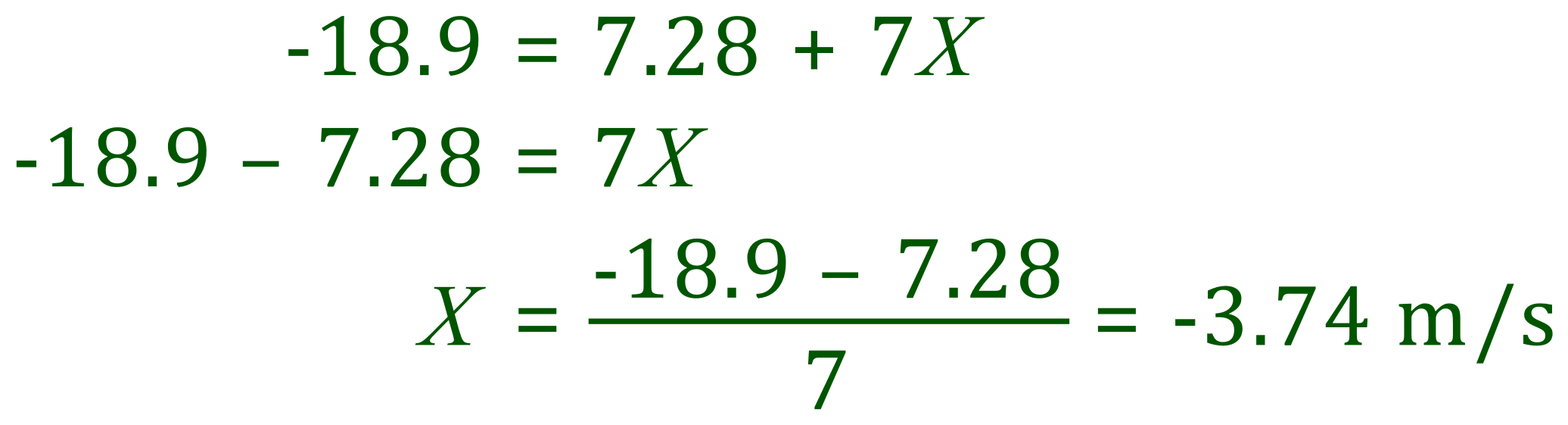
Therefore the BLUE ball was approaching from the RIGHT at 3.74 m/s (the negative sign is only a convenience, we can't have a negative velocity in reality).
Q11. This is a two-part question. A snooker player strikes the cue ball with the intention of potting the green ball for 3 points. However, the shot misses and the green ball collides with a stationary blue snooker ball. Both green and blue balls have a mass of 160 g. Before the collision, the green ball was moving to the right at 0.5 m/s.
(a) calculate the total momentum of the two ball system before the collision.
(b) after the collision, the green ball continues to move to the right at 0.1 m/s, what is the velocity of the blue ball after the collision?
A11. The first thing to do in a question like this is to establish exactly what you've been given, sometimes it can be helpful to sketch out a diagram and label it with the values that you've been given:

(a) The total momentum before the collision:
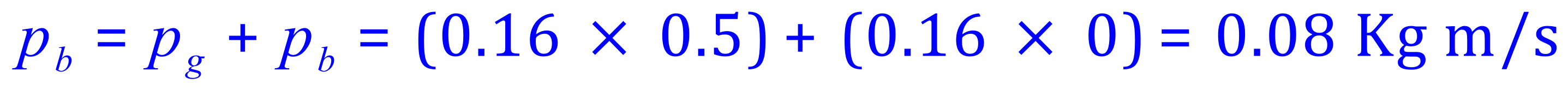
(I have chosen to show in the calculation the ZERO momentum possessed by the blue ball as a mathematical convenience).
(b) After the collision, the green ball has slowed down to 0.1 m/s, it has "lost" momentum and now possesses:
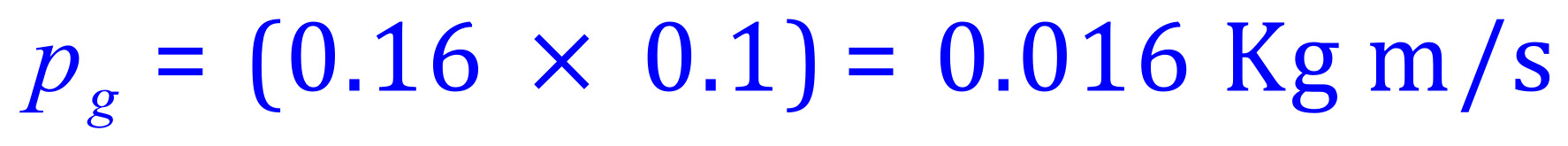
The law of conservation of momentum tells us that the "lost" momentum has been transferred to the blue ball, which now possesses:

As we know the mass of the blue ball, calculation of its velocity is quite simple:
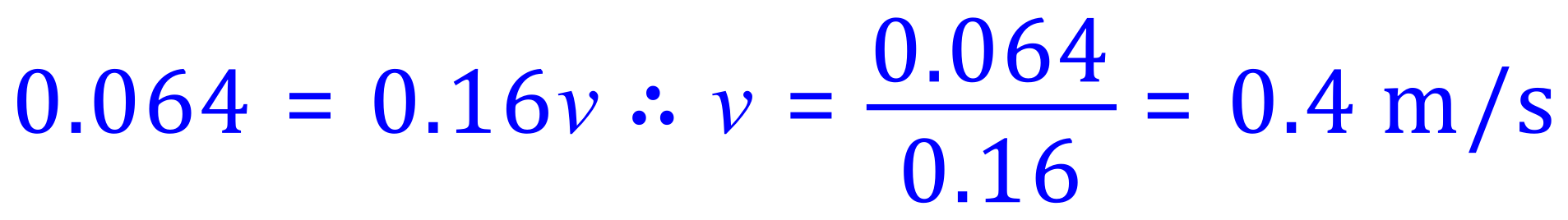
Therefore the blue ball moves at 0.4 m/s to the right.
Back To >> Questions <<
Back To >> Defining Momentum <<