Half Life
Q. A radio isotope has an initial activity of 840 Bq (Becquerel = 1 radioactive / nuclear decay per second). What will the activity of the sample be after 5 half lives, as a percentage of the original?.
A. From the above equation:
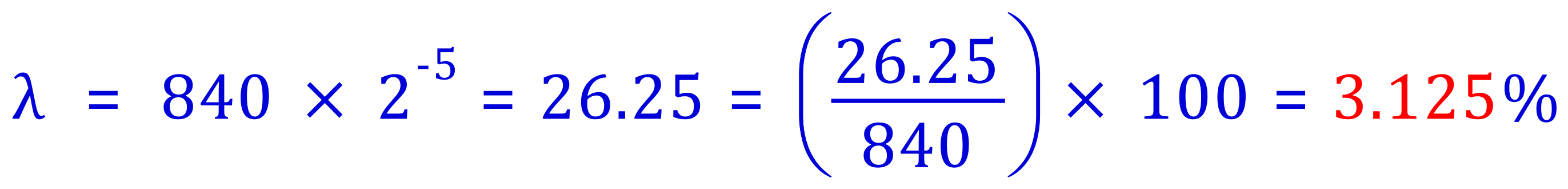
Q. A radio isotope has an initial activity of 1200Bq, after 7 hours it has decreased to 4.6875 Bq. What is the half life of the isotope?
A. Work out the number of half lives that the sample has passed through:
![]()
8 half lives in 7 hours, therefore the half life of the isotope is:
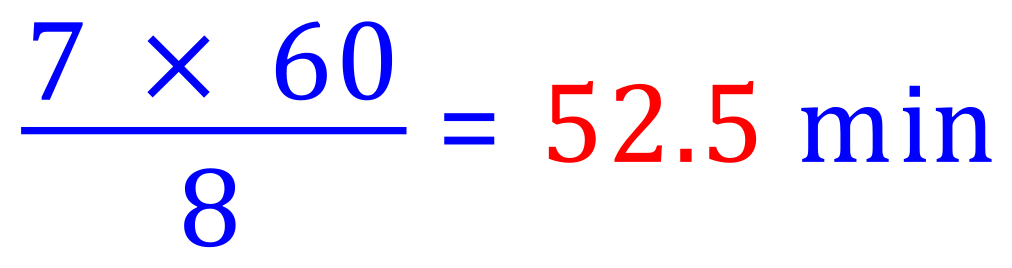
Q. A sample of Caesium-137 is found to have an activity of 24 Bq. Caesium-137 has a half-life of 30 years. What will the activity be, in Bq, at 90 years?
A. 90 years is 3 half-lives, therefore the decay "timeline" would be:
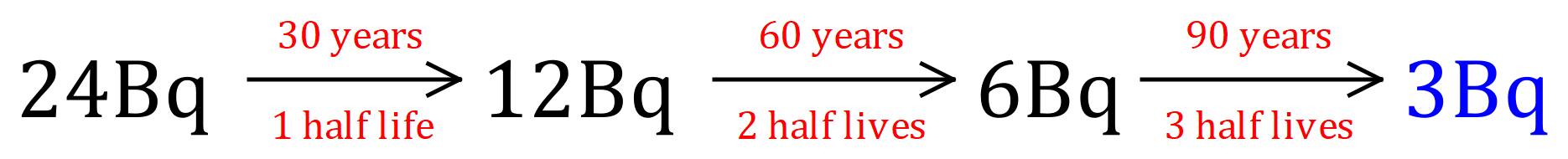
Q. Caesium-137 decays to an isotope of Barium-137. From this information alone, suggest the type of decay taking place. Show the equation for your decision.
A. We can rule out alpha decay, as the mass number would decrease by 4 and the atomic number by 2, in such a case the "daughter" nuclide would be an isotope of Iodine. We can also rule out gamma emission as there is a change in atomic number, an increase of 1 which suggests a "subtraction of -1". The only emission to produce an increase in atomic number would be "beta" emission as a neutron decays to a proton, emitting an electron and an antineutrino.
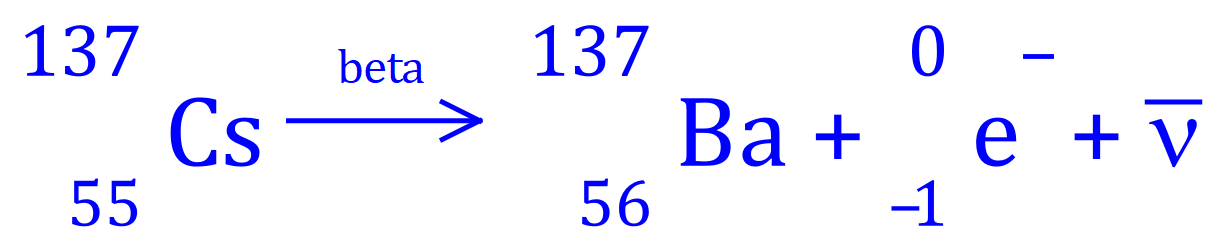
Q. The half life of a radioactive isotope is 27 years. How long will it take for a 2g sample of the isotope to reduce in mass to 0.25g ?
A. There are a couple of ways that this can be completed. Looking at the "half life reductions" we can see that the mass reduction is complete in 3 half lives (the number of arrows represents this value).
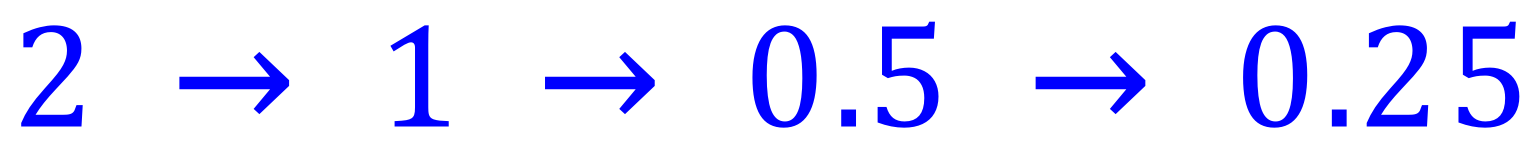
Each half life is 27 years so 3 half lives is 27 x 3 = 81 years.
Secondly, but a little more complicated, is the relationship between initial and final masses and half lives:
If ..... initial mass = "x", final mass = "y" and number of half lives = "n" :
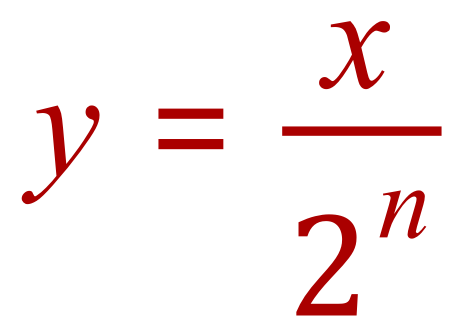
So substitution of our known values gives us this:
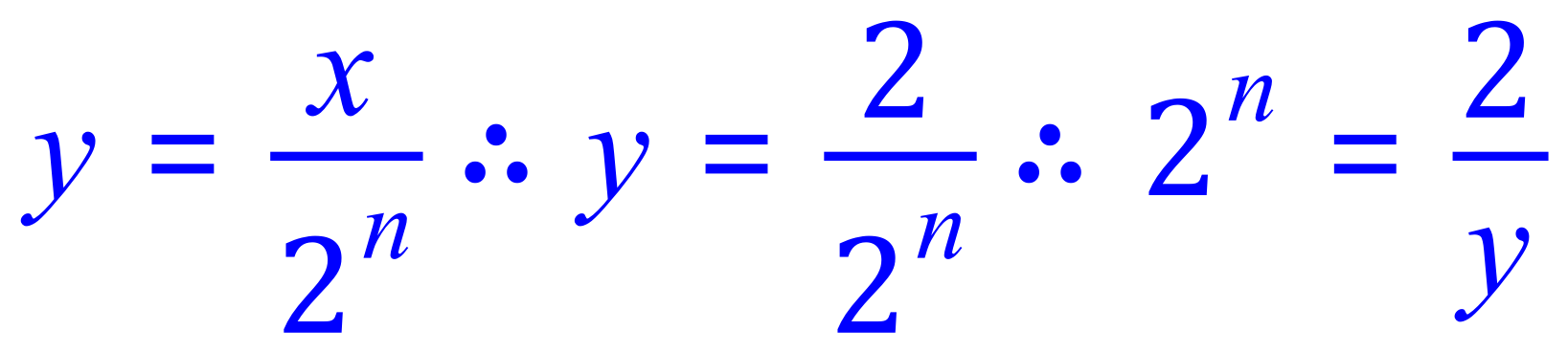
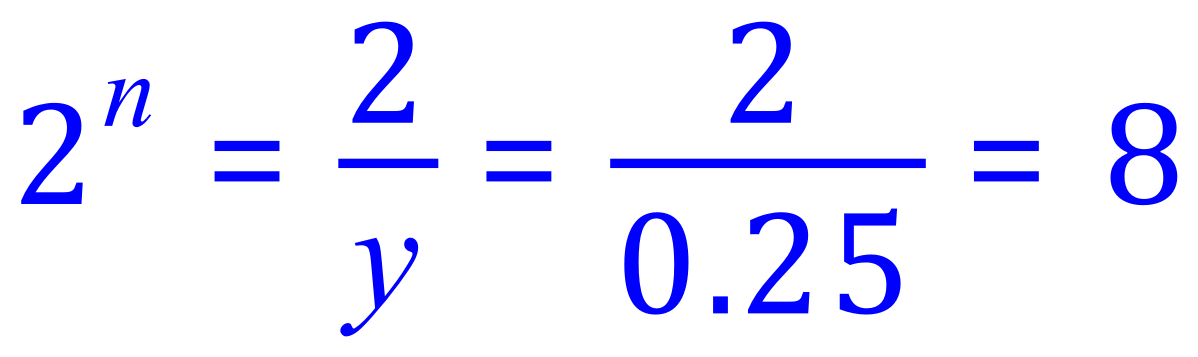
Finally:
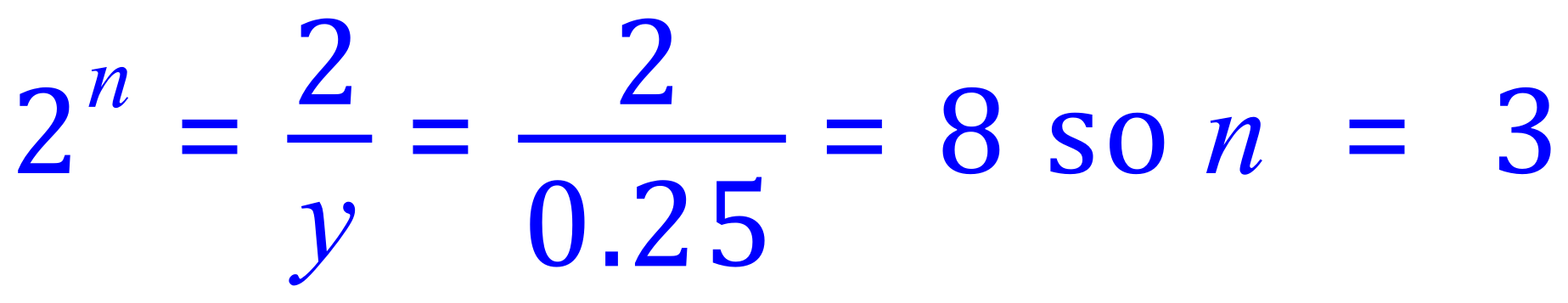
Each half life is 27 years, so 3n = 81 years.
Q. The activity of an isotope falls from 600 Bq (becquerel) to 150 Bq in 10 days. What is its half-life?
A. We are looking for "n", we have been given "x" = 600 Bq and "y" = 150 Bq:
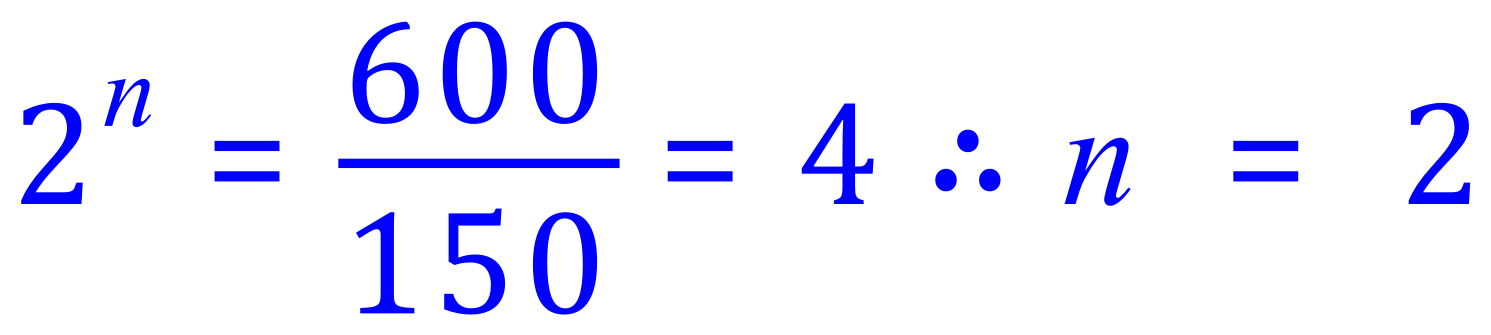
2 half lives = 10 days, so one half life is 5 days.
Q. An isotope has a half-life of 30 years. Estimate how long it will take for the number of nuclei to decay to below 200 if the starting number is 8,000?
A. This question is best attempted using the "arrow" method of half lives as the answer is going to be inexact:
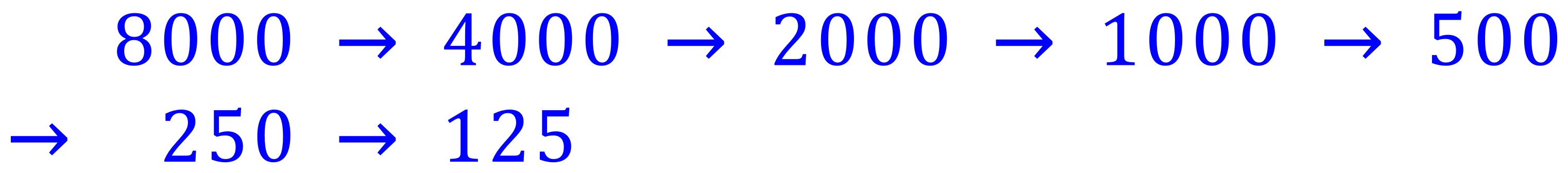
The number of arrows is 6 but the required "range" comes between numbers 5 and 6, so the answer would be quoted as "between 5 and 6 half lives", or "between 150 and 180 years"
Q. A radioactive isotope has a half life of 30 minutes, what fraction of the substance will NOT have decayed after 1 hour?
A. Remember that "half life" involves the repeated "halving" or "multiplication by 1/2", with this in mind......
After 1 half life we have 1/2 of the original amount.
After 2 half lives we have 1/2 x 1/2 or 1/4 of the original amount.
So after 1 hour (2 half lives) we will have 1/4 of the original amount left, the answer is therefore 1/4
Q. A substance has a half life of 3 hours, what fraction of a sample will have decayed after 6 hours?
A. 6 hours is 2 half lives:
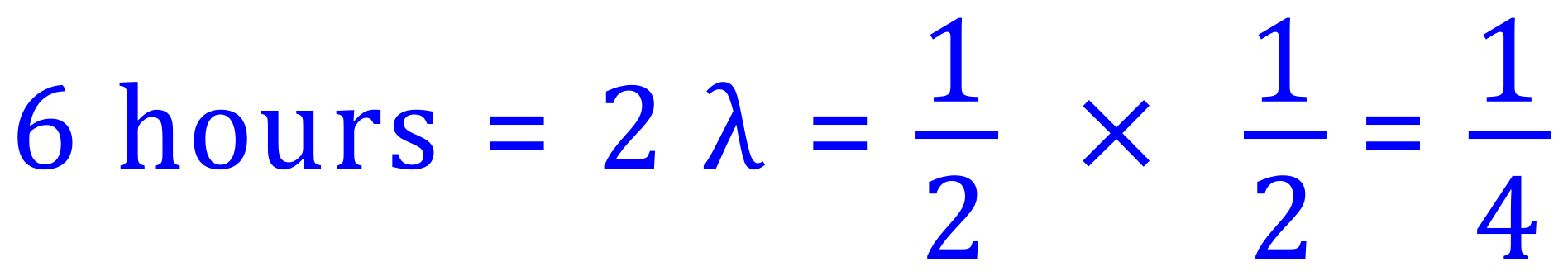
If we have 1/4 of the sample left after this time, then 3/4 is the fraction that WILL have decayed.
Q. A scientist records an activity of 200 counts per minute coming from a radioactive source. This measurement takes place at 12:00pm. At 3.pm she takes another reading which is 25 counts per minute. What is the half life of the substance?
A. The activity drops:

or 3 half lives. If the sample passes through 3 half lives in 3 hours, it has a half life value of 1 hour.
We could also use the "relationship" expression here:
"x" = 200, "y" = 25 and the time is 3 hours:
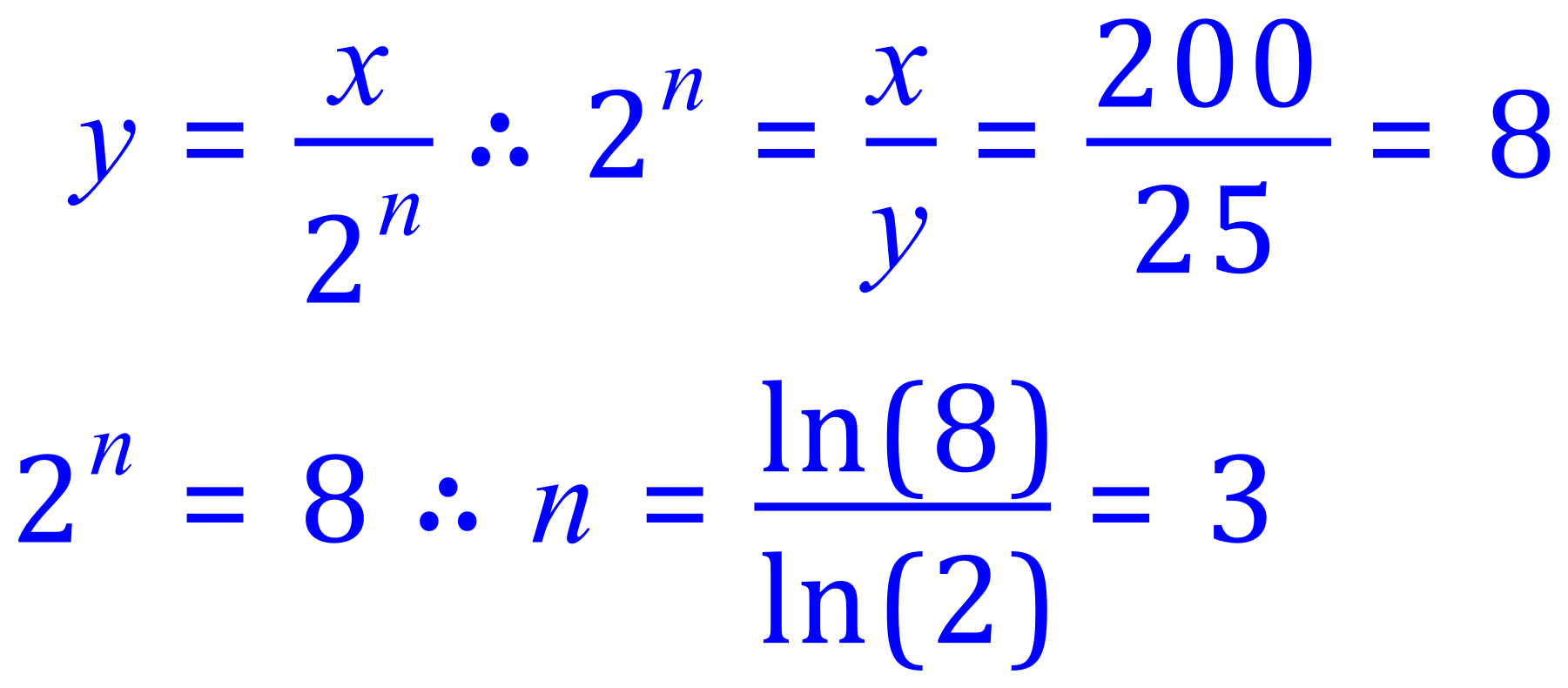
3 half lives in 3 hours leads to a half life of 1 hour as before.
Back To >> Questions <<
Back To >> Half Life <<