Half Life
We have now briefly discussed the different types of radioactivity that we can encounter, but how long does this go on for? Is a radioactive substance always radioactive, or does it stop being radioactive at any point?
To answer these points, it is arguable that radioactivity/radioactive emission never stops but it does get less and less over time. A radio isotope will eventually reach a stable state where nuclear decay (arguably) ceases, but in many cases this takes a very long time. Radioactive decay is caused as a result of nuclei breaking down and each time a nucleus does this to become a stable nucleus, there are less and less of them left behind. Because radioactivity (arguably) never actually stops we can't say that it's "come to an end", if you look at the chart you will see that although the numbers get less and less they never reach zero.
As a result of this, physicists look at the length of time it takes for a radioactive substance to reduce to half of its "potency" for want of a better word, in other words how long it takes for the source to decay to "half strength". This is known as the "half life" and can range from fractions of a second to millions of years, depending on the substance concerned.
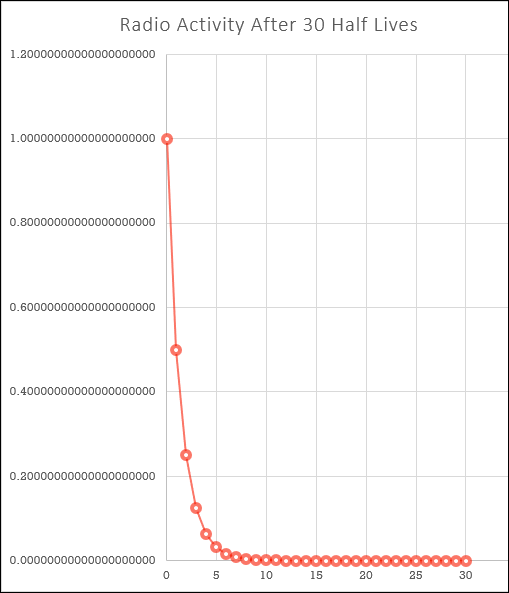
Let us say that a radioactive substance starts at a strength, or activity of "1". After a certain length of time the substance will have dropped to half strength, and the time it takes to do this is given as "one half life". As you know from mathematics, half of a half is a quarter and so the time it will take our radioactive substance to drop to a quarter of its original strength will be 2 half lives.A further half life passes and our radioactive substance will have now dropped to 1/8 of its original activity. The table below shows 30 half lives, shown graphically above but numerically for your information:
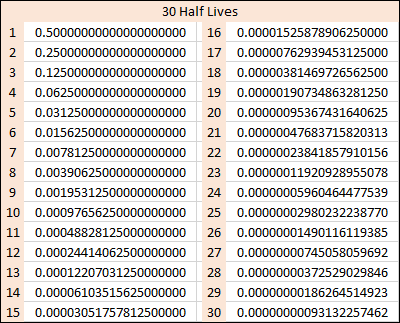
Look at the table. After the first half life the activity of the sample is 0.5 (a half) as you would expect, after the second half life it becomes 0.25 (a quarter) and after a subsequent third half life it becomes 0.125 (and eighth). Half life number four takes us to 1/16 and so forth.
It's probably not quite so easy to see it graphically, but numerically you can see that even after 30 half lives we still have a positive number, we have not reached zero and we never will.

If you want to take this one step further, look at the picture above and count the number of brown dots, each of which represents an unstable nucleus. After the first half life starting from the left the number is reduced to half, and subsequently reduced to half again, from 16 to 8 to 4.
Remember that this can never reach zero, half of 4 is 2, half of 2 is 1 and half of 1 is 0.5. We then start to enter the very long decimal numbers in the table above. Is there a mathematical way that we can represent this? Well, of course it wouldn't be good science if mathematics didn't get involved somewhere.
Let's take a quick look at index powers. Consider "what is 2 raised to the power of 0?
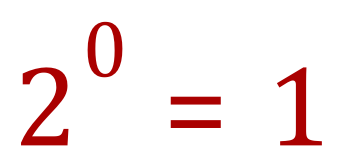
In fact, any number raised to the power of zero is also one, but the reason I chose to is that it features prominently in "half" as in "half life" now read on :-)
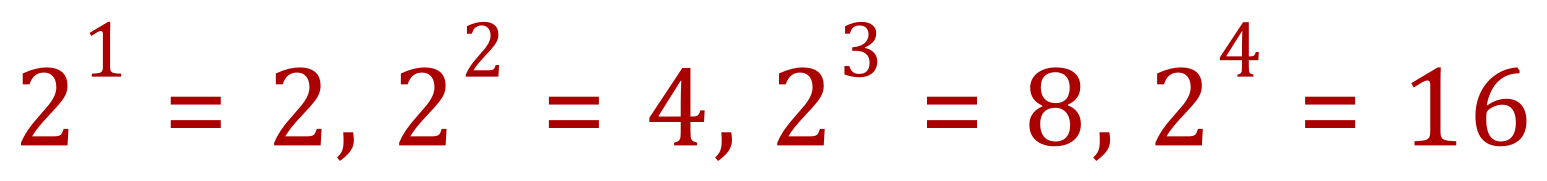
You might be thinking to yourself now "yes, okay I know this" but you might not, at this stage, know where I'm taking it. Previously, and as shown in the table, we talked about half, quarter, eighth, sixteenth and so as a radioactive substance went through progressive half lives. Can we represent these fractions in the same way?
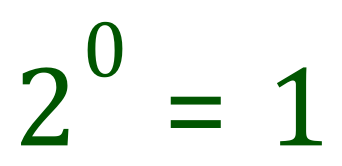
Yes, we've been there and done that but let's move on to something a little bit different:

Have you noticed any relationship between the index number and the result of the calculation? If we take the absolute value of the index number (that is we ignore the negative sign) and compare it to the result of that particular part of the equation, and then refer to the half life table previously there is a correlation.
The activity of the radio isotope after 'n' half lives is therefore:
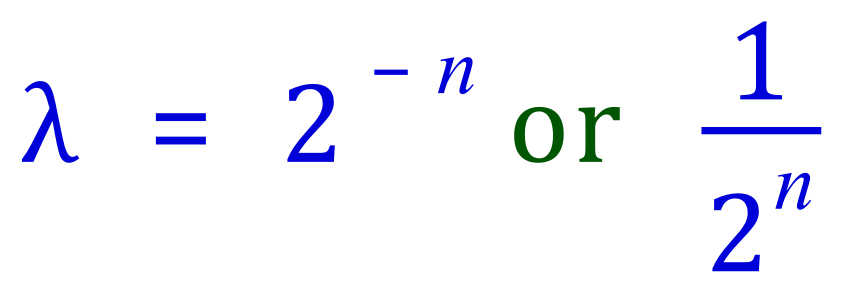
Of the original activity.
>> Questions <<