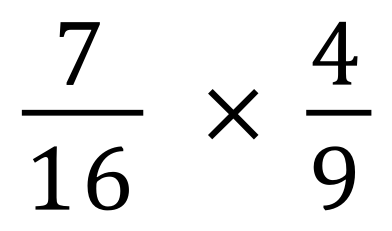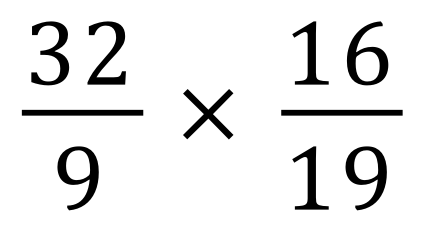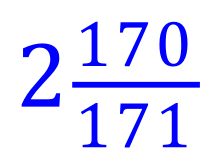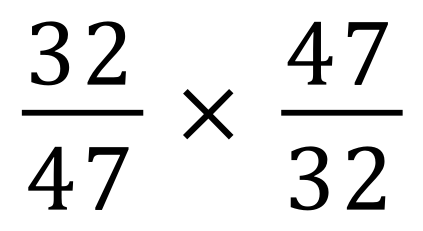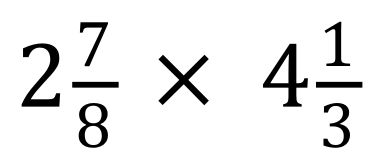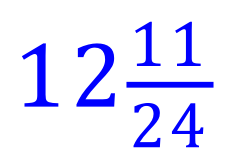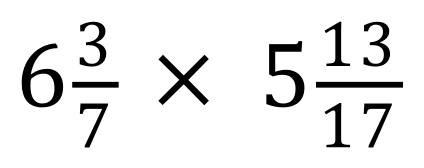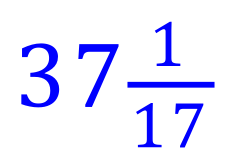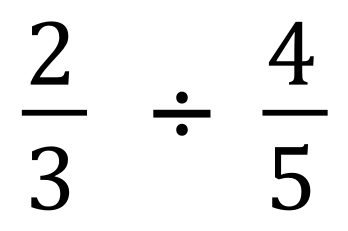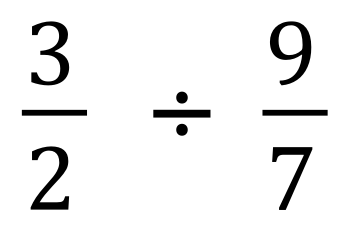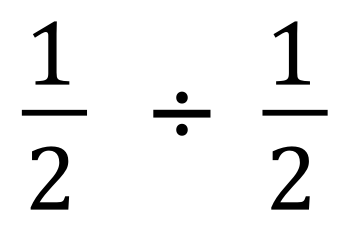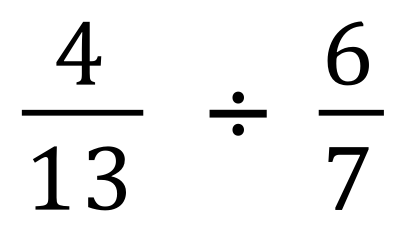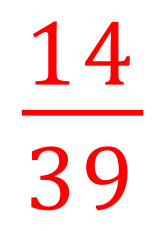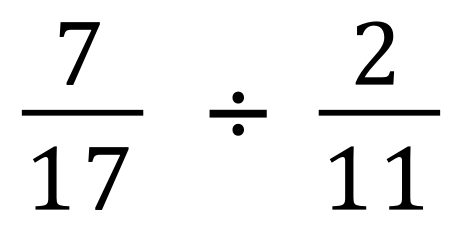When we come to multiply and divide fractions, we quickly realise that it is easier to do this than it is to add or subtract them. The reason for this is in the addition and subtraction of fractions, we have to first convert to a common denominator, then perform the additional subtraction, and then simplify whereas with multiplication and division there is no common denominator step.

Let’s take a look at the multiplication of a simple fraction:


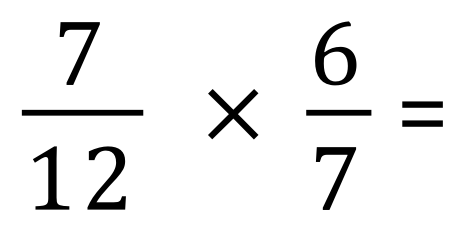
to multiply a fraction, as I said before we do not need to bother with a common denominator, we simply multiply the numerators together which produces the numerator of the result, and then we multiply the denominators together to give us the denominator of the result. We do have 2 simplify and where necessary convert the answer to a mixed fraction.




Exercises


Calculate the result of each of these fractional multiplications, state your answer in its simplest form and as a mixed number if necessary.


(Use your calculator if you want to)


Dividing Fractions


Essentially, there isn’t a specific method for doing this, we adopt the principle called “invert and multiply” where we take the 2nd fraction (known as the “divisor”) ,turn it upside down and then perform a multiplication like we have previously.


Here’s an example:

In this particular case, if we invert the divisor and multiply we have this expression: 




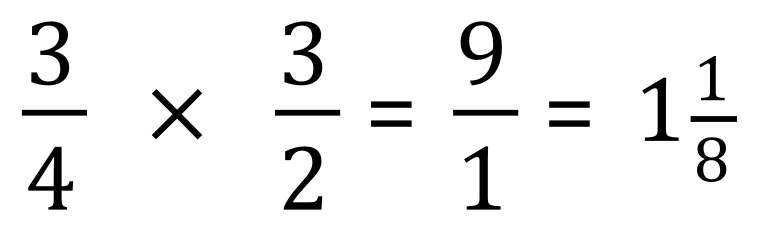
So the answer to the initial problem “3/4÷2/3” works out to be “1 1/8”


Exercises


Calculate the result of each of these fractional divisions, state your answer in its simplest form and as a mixed number if necessary.

(Use your calculator if you want to)