Multiplication of Matrices
Matrices can be multiplied together, but as mentioned previously certain rules must apply depending on the operation being considered. In the case of multiplication matrices can be multiplied only if the number of columns in the first matrix equals the number of rows in the second.
An example will help us here:
Let us consider two matrices, A and B, these matrices can only be multiplied together if the number of columns in A is equal to the number of rows in B.
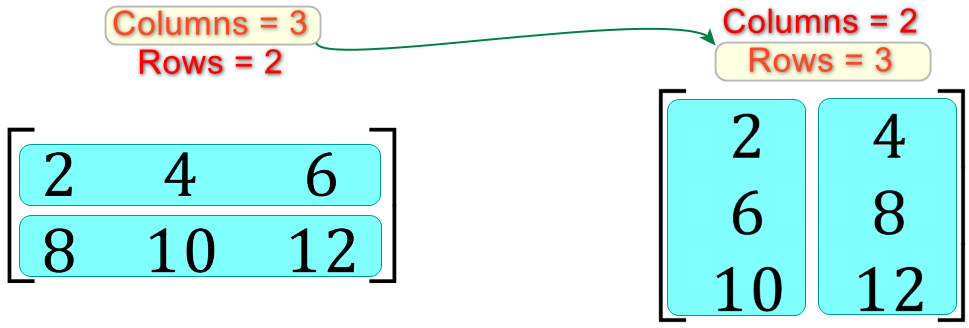
As you can see, the matrix on the left can be multiplied by the matrix on the right because the rule with regard to columns and rows is satisfied. In the following case, the matrices could not be multiplied together:
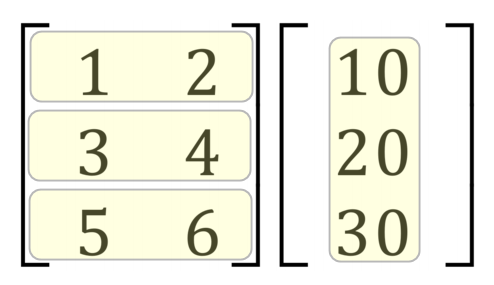
Clearly in the case of the second set of matrices (the ones highlighted in yellow) the number of columns in the left matrix is 2, with 3 rows whereas the right-hand matrix has 3 rows but only 1 column.
The slightly confusing part is about to start, we have talked about (albeit briefly) the "cans" and "can'ts" of matrix multiplication, but not actually how to do it. We'll look at this now by working out the result of the matrix set in blue above.
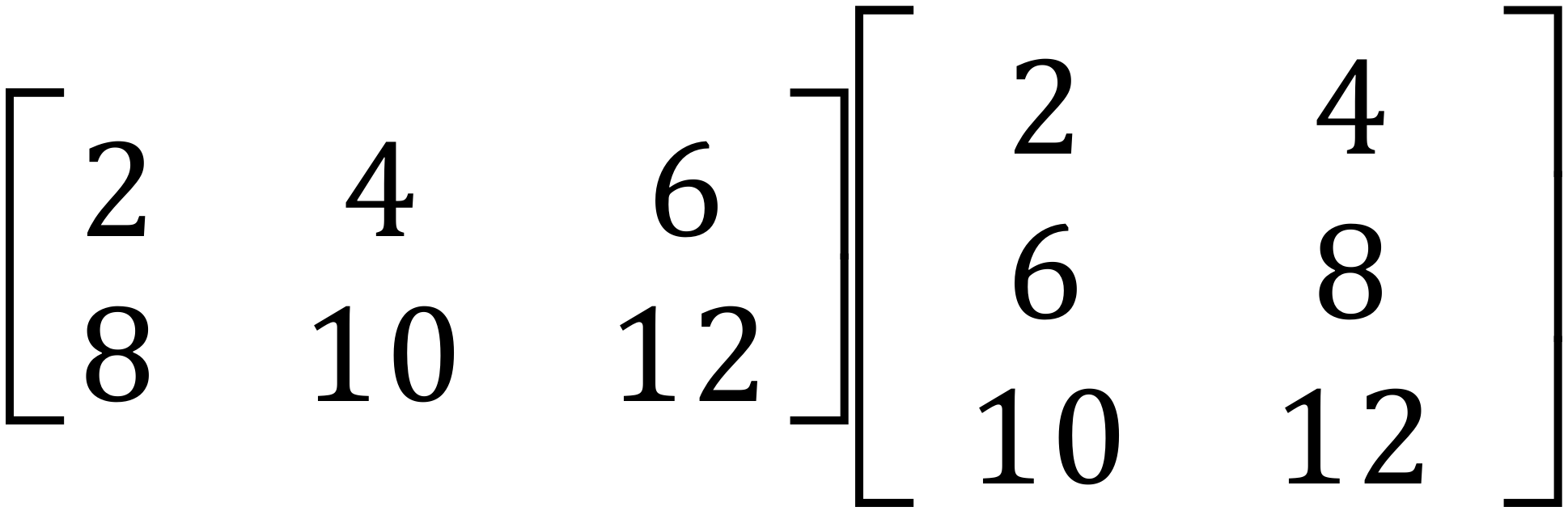
|
Left Side Matrix |
Right Side Matrix |
||
|
R |
C |
R |
C |
|
2 |
3 |
3 |
2 |
|
|
As these are equal it means that these |
|
|
|
The outer bounds determine the size of the resulting matrix (in this case a 2x2 will be formed.) |
|||
|
2 |
x |
2 |
|
Now let's see how its calculated. By no stretch of the imagination can this part be called "easy". When you first start looking at matrices it can be very confusing to keep in mind which particular elements are multiplied together to make the subtotals, and in which order.
Fortunately there are a number of good tutorials available online, one that I've chosen to use here involves laying out the matrices on a two-dimensional plane and then performing the arithmetic on rows and columns which "virtually" intersect.
An example will help.
|
|
|
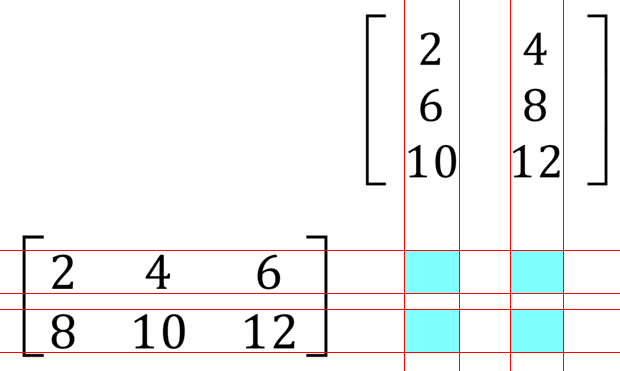
The picture on the left shows the matrix question as you may receive it, and the picture on the right shows the same problem laid out ready to be solved. The rules of matrices show that the left and matrix is "2×3" and the right matrix is "3×2", which by combination will give us a resultant matrix of "2×2" as shown by the light blue shaded squares. It is inside the light blue shaded squares that we will enter the results of the arithmetic.
Each row and each column show an intersection, you can choose any intersection point (Blue Square) but I would advise that you start from top left to bottom right in that order.
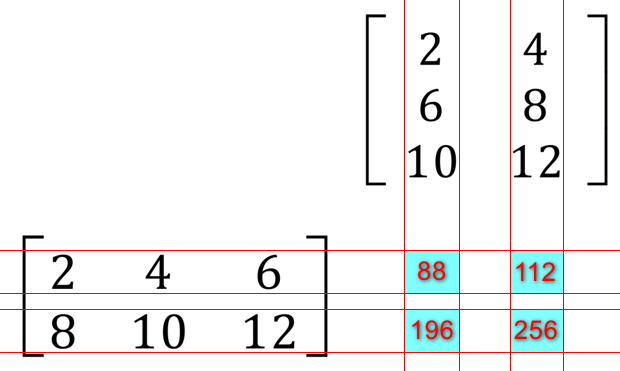
|
Top Left |
2x2 |
4x6 |
6x10 |
88 |
|
Top Right |
2x4 |
4x8 |
6x12 |
112 |
|
Bottom Left |
8x2 |
10x6 |
12x10 |
196 |
|
Bottom Right |
8x4 |
10x8 |
12x12 |
256 |
Of course the numbers in the extreme right hand column (in red) are the totals of the previous three. We now insert each total into its "Blue Square" in the resultant "2×2" matrix:
|
|
|
And this is the final answer, you will arrive at a "2×2" matrix with the element values as shown. This is perhaps the simplest method that I have found so far for multiplication of matrices.
>> Questions <<