Newton's Second Law
Q1. An object with a mass of 6.5 kg accelerates 12.3 m/s2 when an unknown force is applied to it. What is the amount of the force?
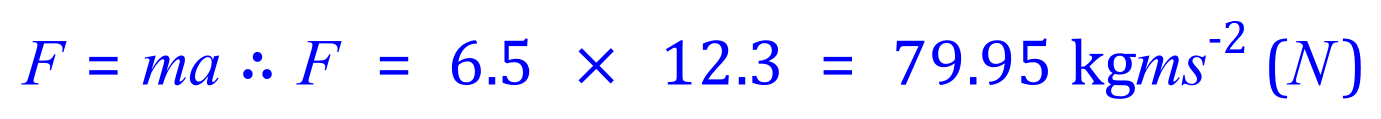
Q2. A car with a mass of 900 kg accelerates from rest with an initial acceleration of 2.5 m/s2. Calculate the resultant force required to produce this acceleration.
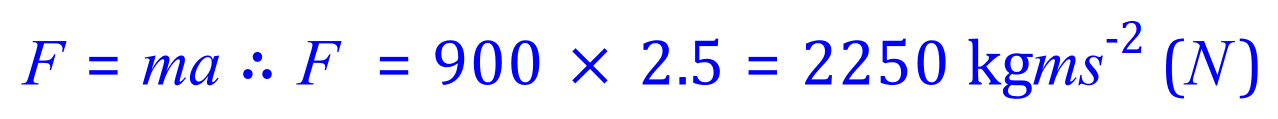
Q3. An object accelerates 7.2 m/s2 when a force of 4.0 Newtons is applied to it. What is the mass of the object?
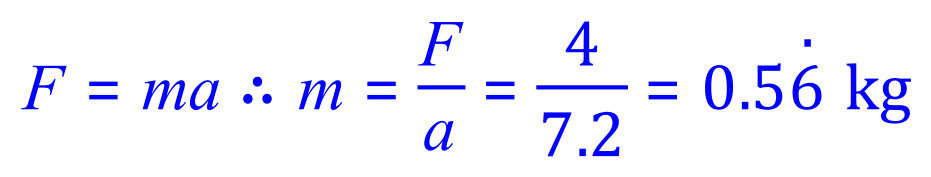
Q4. A speed boat in the water experiences an acceleration of 0.524 m/s2. The boat's mass is 842 kg. What is the force that the boat's engines are putting out?
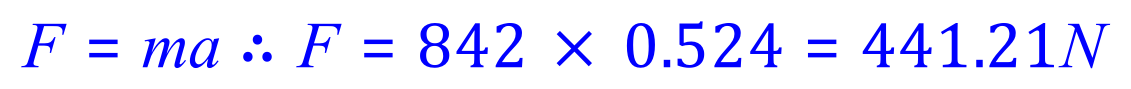
Q5. A very fast car accelerates from a rest to 32 m/s, (71.68 mph), in 4.2 seconds. What is acceleration of the car and how many gʼs is this?
Using one of the equations of speed:
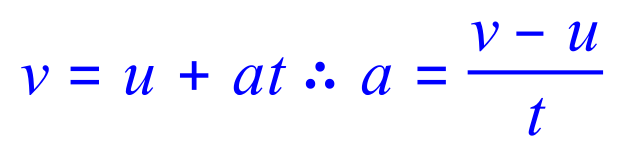
We substitute our known values. 'u' is 0 as the car is initially at rest, 'v' is 32 /ms and 't' is 4.2s:
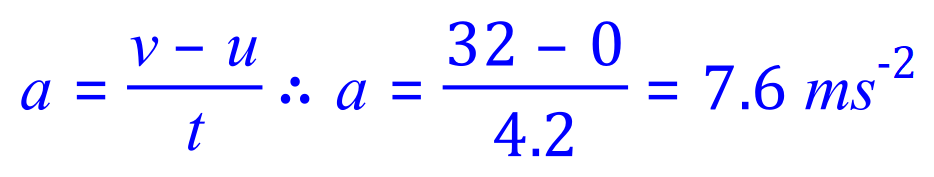
The second part might be new. In calculations involving the acceleration due to gravity 'g' you will often be given the value of 10, 9.81 or 9.8 and it is usually given in newtons per kilogram depending on the question you are being asked. Other units for 'g' are 'metres per second per second' as it is of course an 'acceleration' involving distance and time. In this question we take the acceleration due to gravity as 9.8 metres per second per second:
The number of 'g' or 'G forces' is calculated thus:
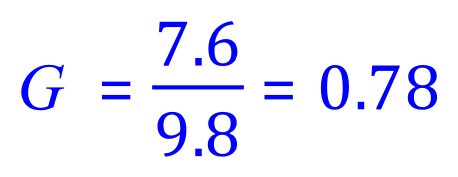
Q6. A stalled car is pushed with a force of 342 N from rest. How far does the car travel in 12 seconds is it's mass is 989 kg?
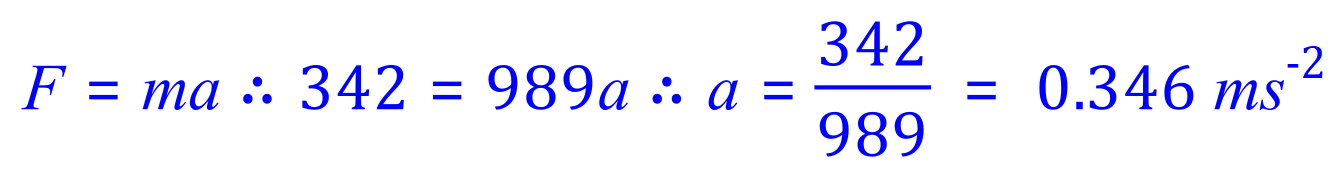
Now that we know the acceleration of the vehicle, we can substitute this into one of the speed/time equations to establish the distance covered:
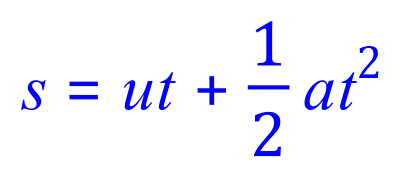
Where 's' = distance, 'u' = initial speed/velocity, 'a' = acceleration and 't' = time.
Since u=0 as the vehicle was stalled (not moving):

Q7. The Space Shuttle travels from launch to 529.2 m in 6.0 seconds. What is the acceleration of the shuttle and how many gʼs is this?
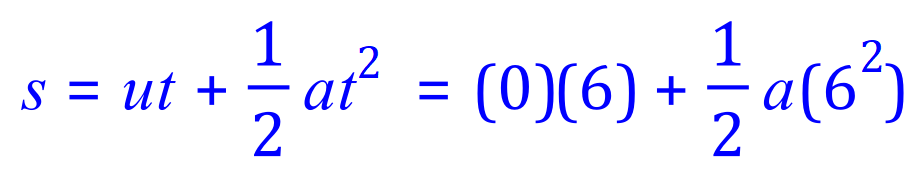
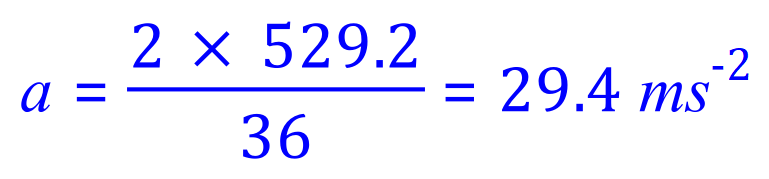
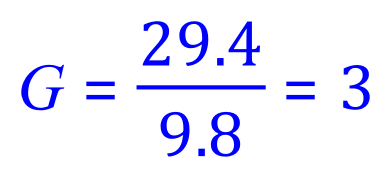
Q8. What force does a car exert if its mass is 1201 kg and the car goes from 5.4 m/s to 16.3 m/s in 107 metres?
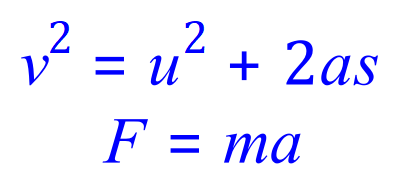
This is essentially a two-part question which requires you to manipulate the first equation involving distance in terms of acceleration. Once you have established the acceleration, substitute this into the equation for force. You will need to develop an eye for this sort of thing, there is another equation which involves distance but of course this time you can't use that because there is a term in that equation 't' which stands for Time. You are not given any information concerning time in the question which renders this particular equation useless. The chosen equation is clearly the right one as you have an initial velocity 'u', a final velocity 'v' and a distance 's' :
Rearranging:
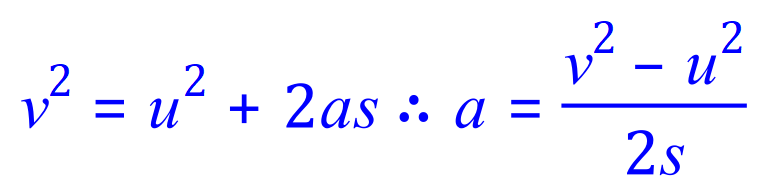
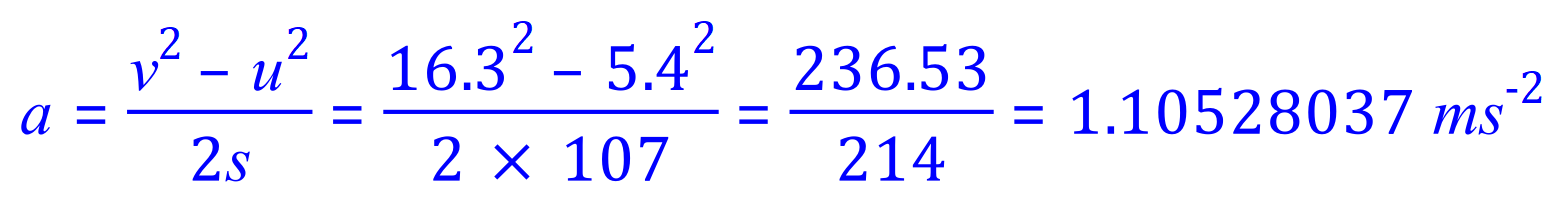
We now substitute our value for acceleration into the standard force equation:
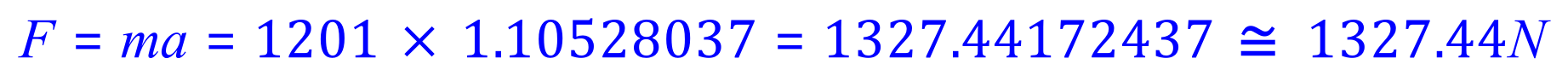
Back To >> Questions <<
Back To >> Newton's Second Law <<