Quadratic Factorisation - When The Coefficient of X Squared > 1
Q1.
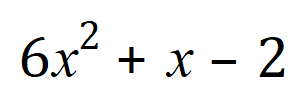
In the same way as in the text examples, we now need to look for two values which when added together come to 1 but which when multiplied together come to -12. Giving this a little bit of careful thought you will come to the conclusion that +4 and -3 will do it.
Rewriting our expression:
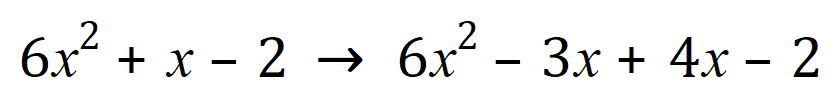
And, in just the same way as before, we now “pair off” and factorise:
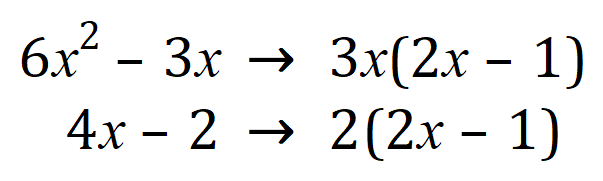
Gathering of the results we now factorise our expression:
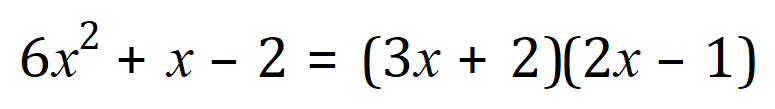
Q2.
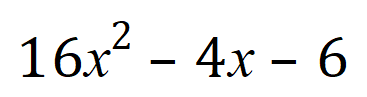
In the same way as in the previous examples, we now need to look for two values which when added together come to -4 but which when multiplied together come to -96. Giving this a little bit of careful thought, and in this laborious case writing out the factors of 96 to arrive at a suitable pair of numbers, you will come to the conclusion (eventually) that +8 and -12 will do it.
Rewriting our expression:
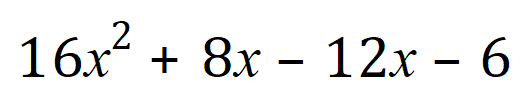
And, in just the same way as before, we now “pair off” and factorise:
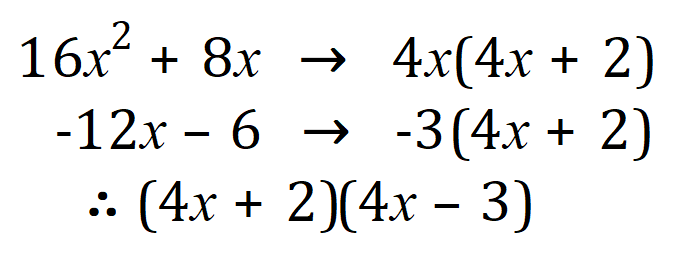
Gathering of the results we now factorise our expression:
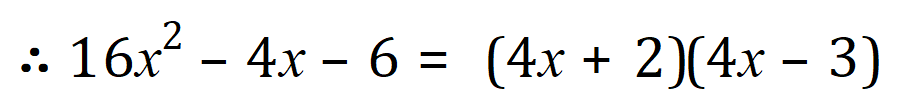
Q3.
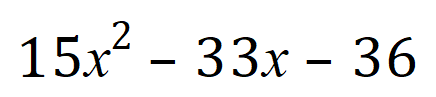
In the same way as in the previous examples, we now need to look for two values which when added together come to -33 but which when multiplied together come to -540. Giving this a little bit of careful thought, and in this laborious case writing out the factors of 540 to arrive at a suitable pair of numbers, you will come to the conclusion (eventually) that +12 and -45 will do it.
Rewriting our expression:

And, in just the same way as before, we now “pair off” and factorise:
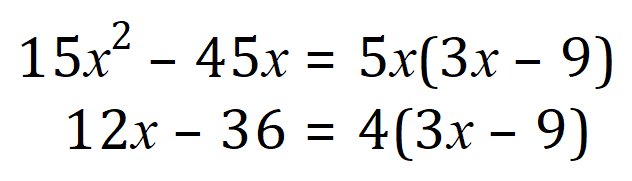
Gathering of the results we now factorise our expression:
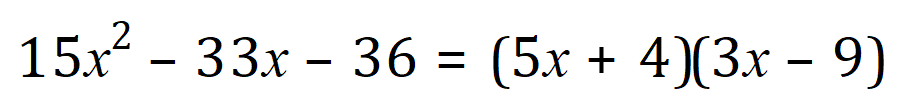
Q4.
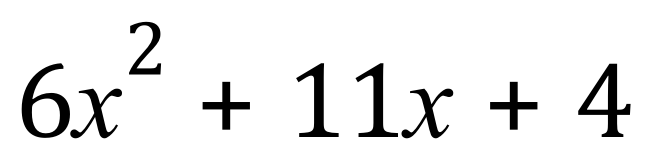
In just the same way as all of the previous examples, we are looking for 2 numbers which, when added together come to +11, but when multiplied together come to +24. Looking at the factors of 24 we can quickly establish that the numbers that we want are in fact +8 and +3, so we split our 'x' component in the usual way:

We pair off the 'x' components with the 'x2' and 'constant' (4 in this example) components, like this:
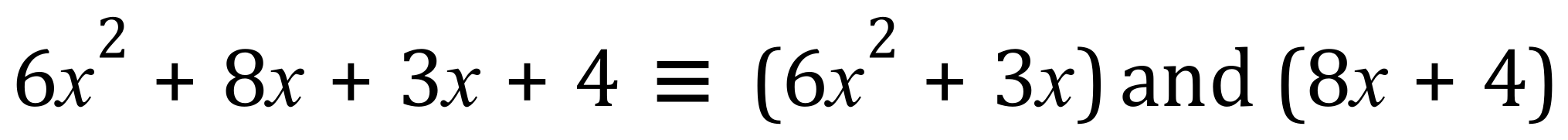
What we need to do now is to factorise both sets of brackets, but in doing so the factor has to be mutual between the 2, in other words it has to be the same factor pulled out of both sets of brackets. We have to do this of course by inspection, let's start first of all with the first set of brackets:
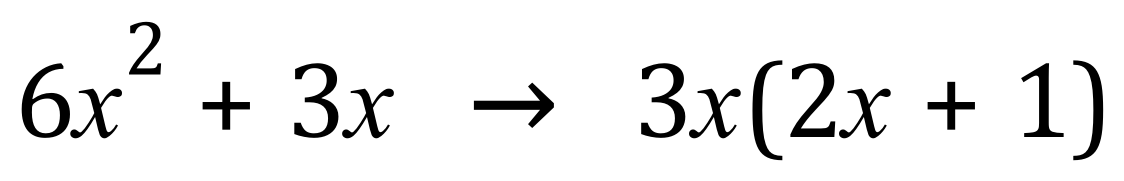
And now with the second set of brackets we have to extract our first identified factor from what we have left:

One of factors is indeed 2x+1 and the other is simply combination of what we have left, which is of course 3x+4
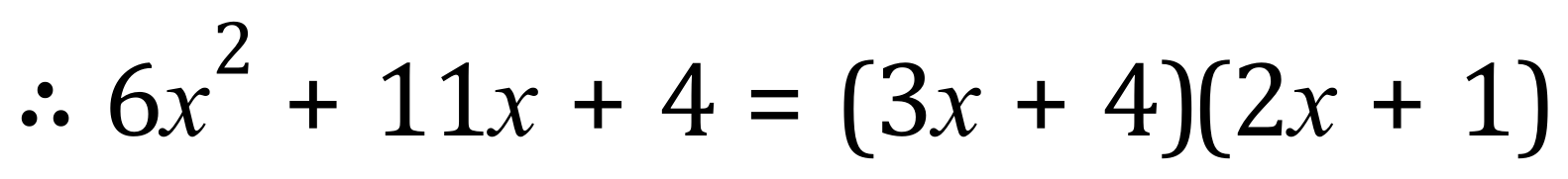
For the remaining 2 examples, I am not going to explain the steps, I am simply going to show them. Follow each step incrementally to make sure you understand where it comes from. If you get stuck, refer back to one of the fully worded examples above.
Q5.
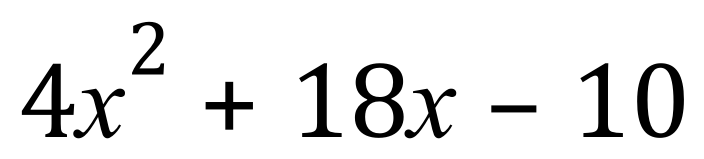
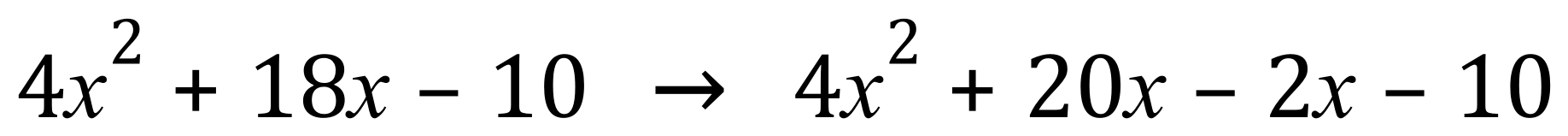

Q6.
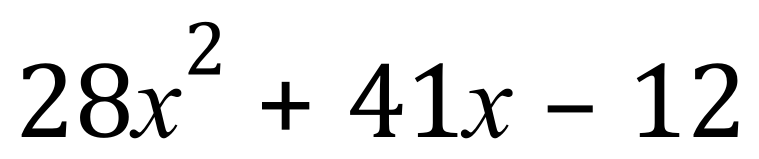
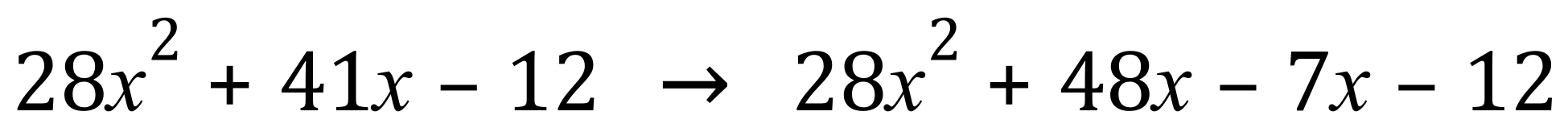
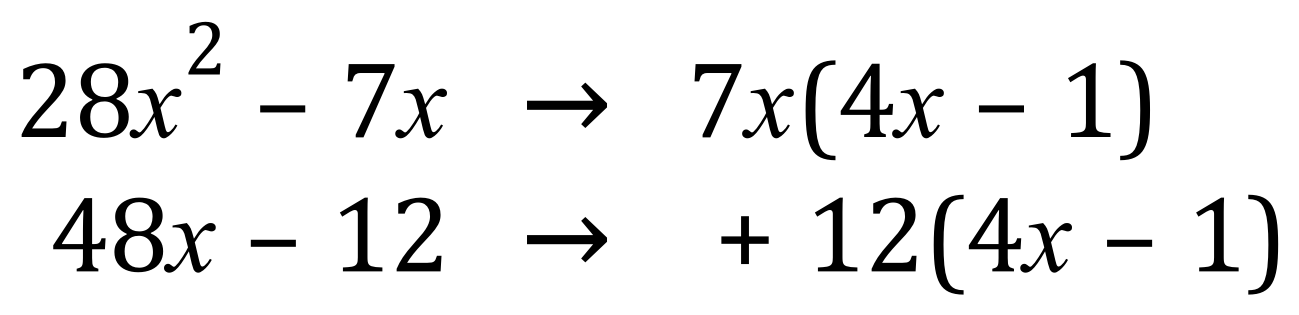
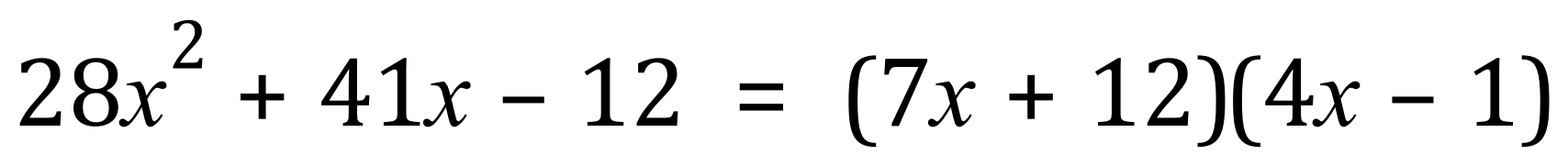
Back To >> Questions <<
Back To >> When The Coefficient of X Squared Isn't 1 <<