Sine Rule
Q1. A triangle has the following properties. Evaluate the remaining two angles in degrees.
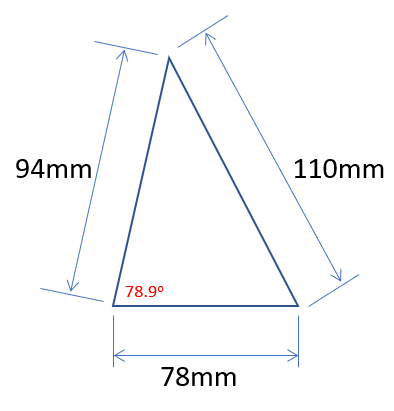
Use the sine rule with the values you are given:
Let A = 94mm, B = 78mm and C = 110mm. From this we have sin c = sin (78.9o)


Angle b = 180 - (78.9 + 60) = 41.1o
Q2. The triangle shown below has the properties stated:
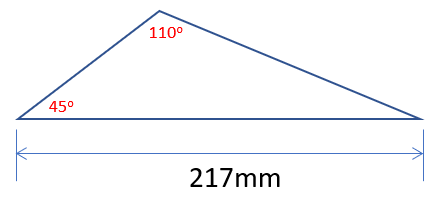
Use the information given, along with the Sine Rule (where necessary) to calculate the remaining angle and the lengths of all three sides.
First of all, if you study the diagram you will see that the angle stated at 45° does not look like an angle of that size. Remember that unless it is specifically stated any diagram you will be given will not be drawn to a scale, so you will be expected to accept the values given and work with them.
Also the question states "where necessary" because to calculate the remaining angle you do not need any complicated mathematics other than the knowledge of the fact that the internal angles of the triangle add up to 180°. In this case therefore the remaining angle is 180 - (110+45) = 25° and this is in fact the answer to the first part of the question.
Part 2 of the question requires us to label the sides and angles according to the sine rule.
Let A = 217mm therefore angle "a" = 110o
Let B = the side opposite 45o therefore angle "b" = 45o
From the Sine Rule:
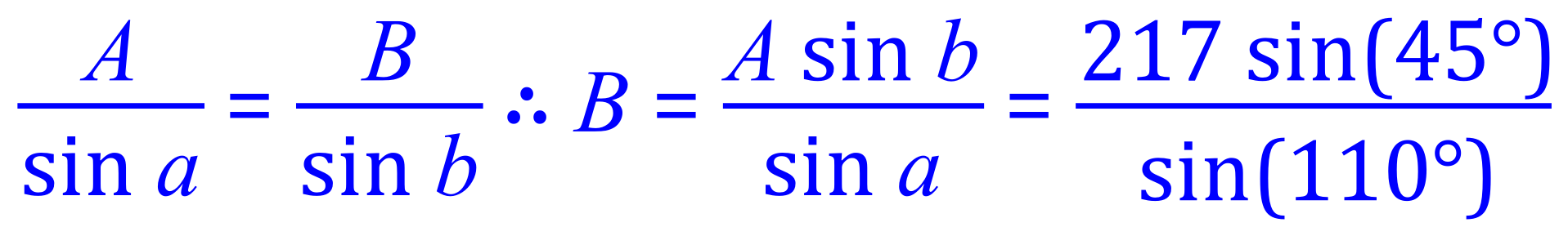
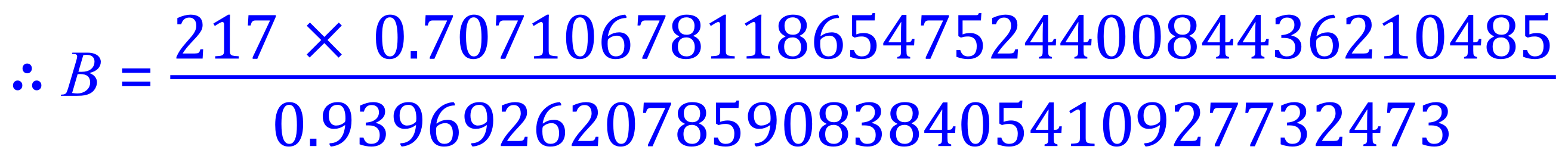
![]()
We now have a result for the length of side B.
As you can see full calculator accuracy has been maintained but the answer has been stated to 0 decimal places. The reason for this is that the question did not ask for any particular level of precision, and based on the fact that the question has not used decimal places in the information it provided, it is common sense to quote any results to the same level of precision.
Let's use the Sine Rule once again to establish a value for the length of side C. We can of course use any values now, so if you wish you may use the newly found value for the length of side B, and the derived value for the angle "c":
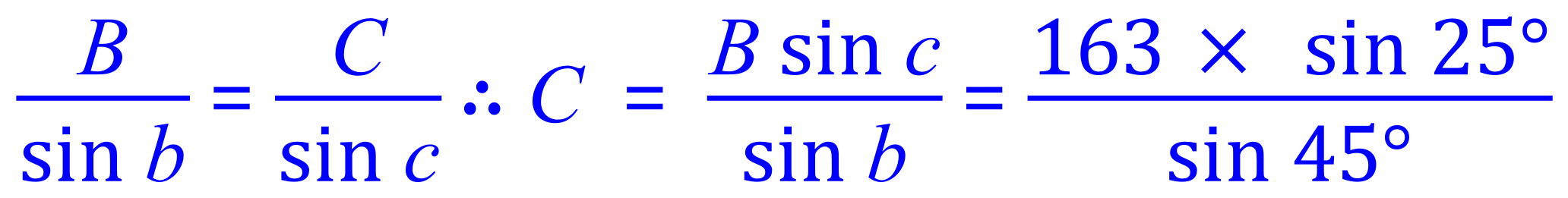
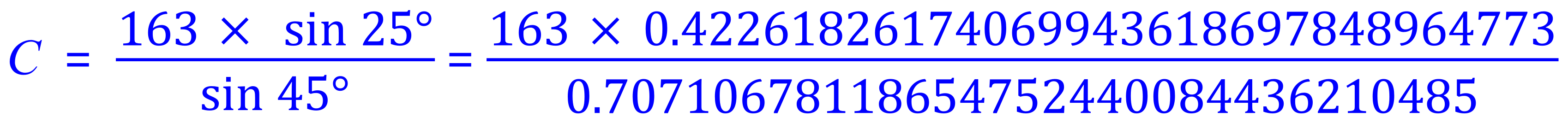
![]()
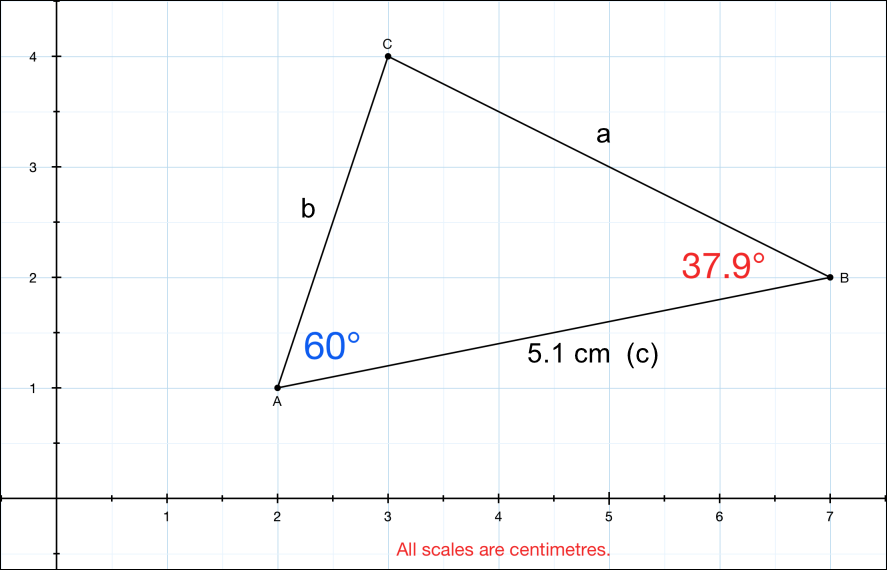
Q3. The triangle ABC is shown on gridded paper, scaled in centimetres. Side AB (c) = 5.1 cm.
Using the information given, and any mathematical method, establish:
- The size of the remaining angle ACB
- The lengths of all remaining sides AC (b), BC (a)
The value of the remaining angle in degrees is quite easy to establish. The internal angles of a triangle add up to 180 degrees, so:
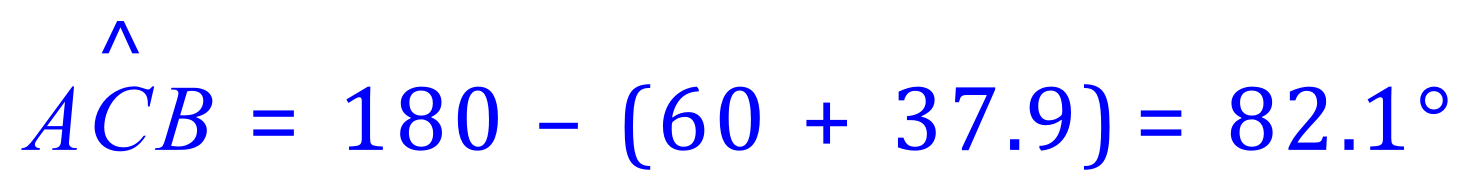
Now we call upon the Sine Rule to start calculating the values of the sides. Given that:
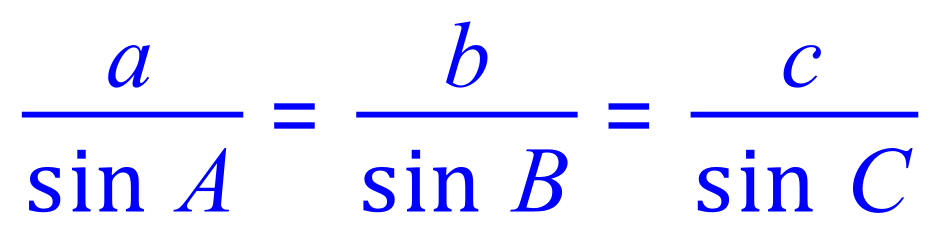
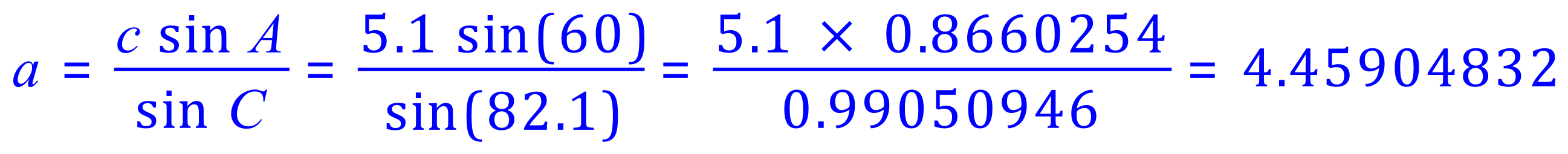
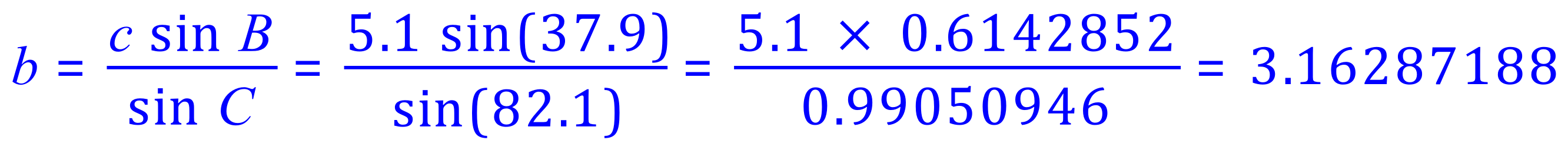
So to 1 decimal place you can state the values:
a = 4.5, b = 3.2 and c as given = 5.1
The question states that the triangle is on gridded paper, and the scale is given. This is usually a sign that some more work is expected. In this case we can confirm our findings from the Sine Rule by using Pythagoras Theorem and the right angled triangles made up from the grid lines, scale and triangle sides:
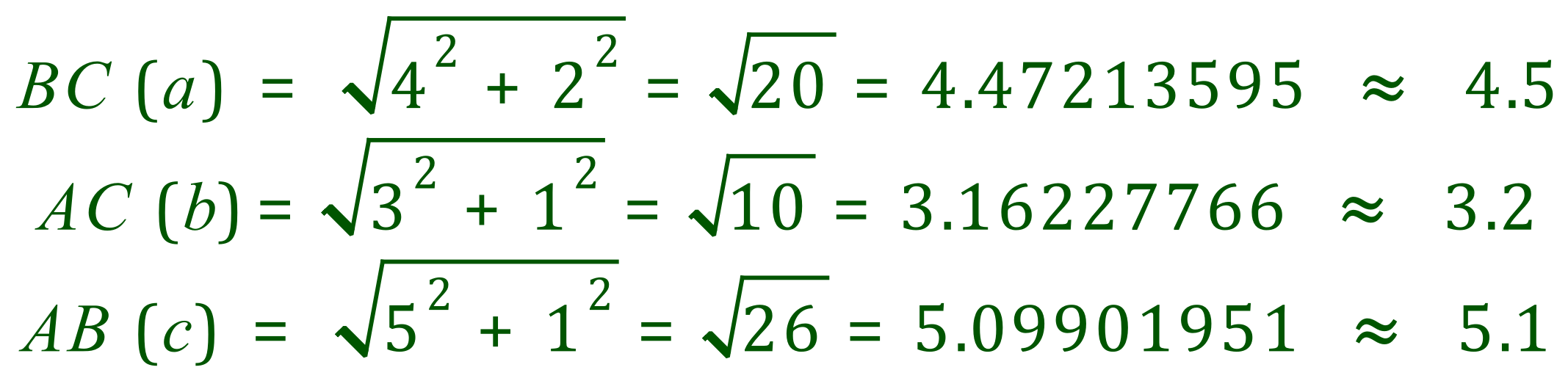
This should show you that your Sine Rule evaluations can be checked against simple Pythagoras!
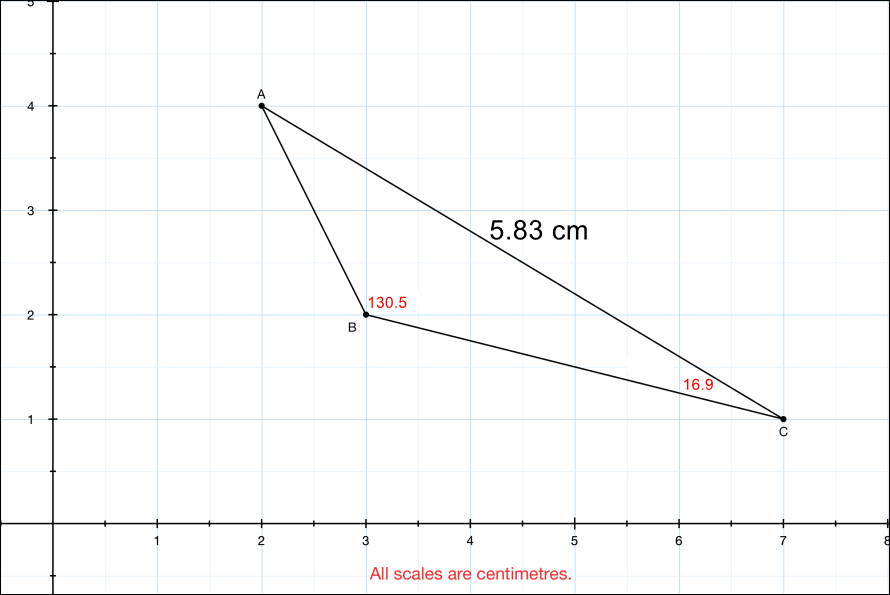
Q4. The triangle ABC is shown on gridded paper, scaled in centimetres. Side AC (a) = 5.83 cm.
Using the information given, and any mathematical method, establish:
- The size of the remaining angle BAC
- The lengths of all remaining sides AB (c), BC (a)
The remaining angle can easily be calculated using then fact that the internal angles of a triangle add up to 180 degrees, so:
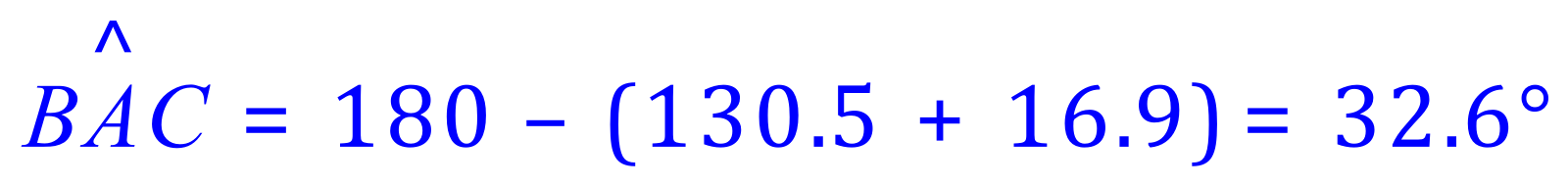
Once again, from the Sine Rule:
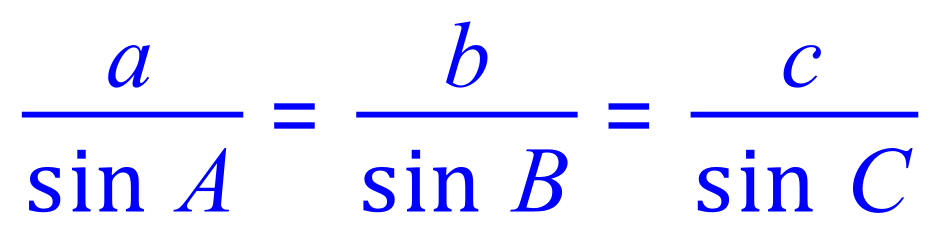
At the moment we only have a value for one of the sides, side "b" so we must establish values for the remaining sides "a" and "c" with the right permutations of the rule:
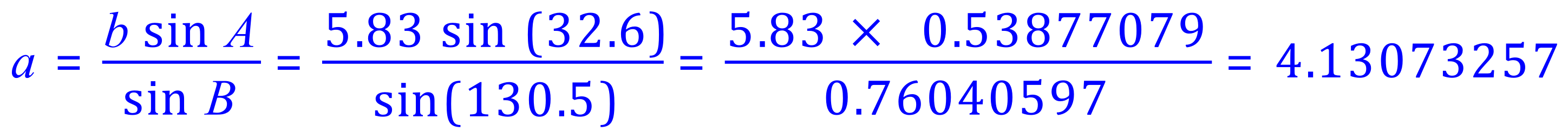

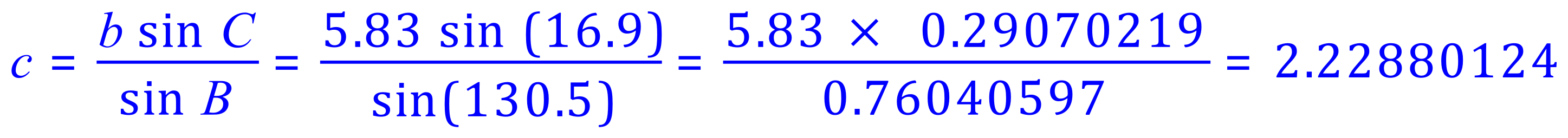
The question states that the triangle is on gridded paper, and the scale is given. This is usually a sign that some more work is expected. In this case we can confirm our findings from the Sine Rule by using Pythagoras Theorem and the right angled triangles made up from the grid lines, scale and triangle sides:
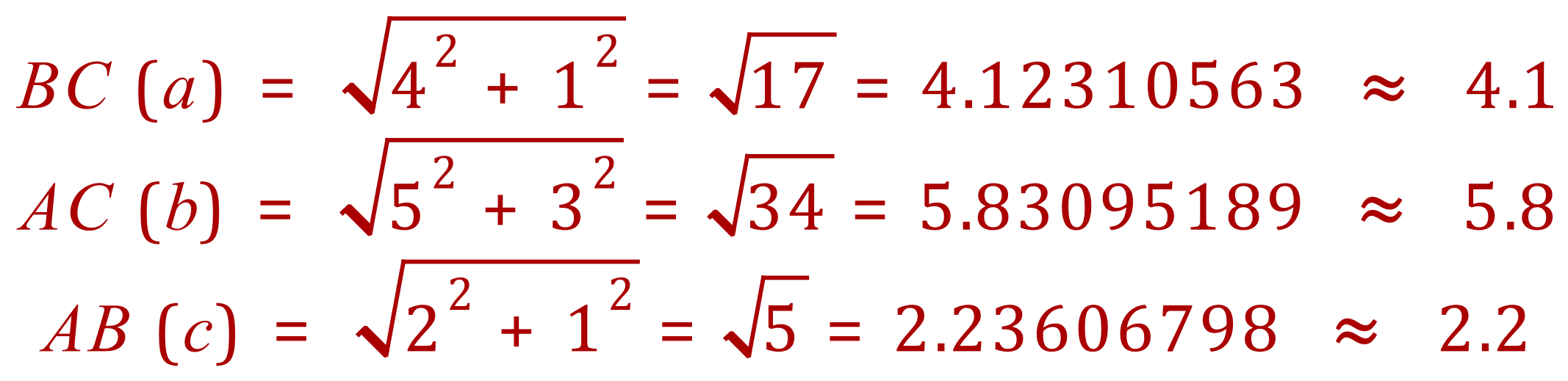
This should show you that your Sine Rule evaluations can be checked against simple Pythagoras!
Go to >> Questions <<
Back to >> Sine and Cosine Rules <<