Cosine Rule
Q1. Given the equilateral triangle shown, and the length of its side as 125mm, use the cosine rule to satisfy yourself that the internal angle shown is indeed 60o
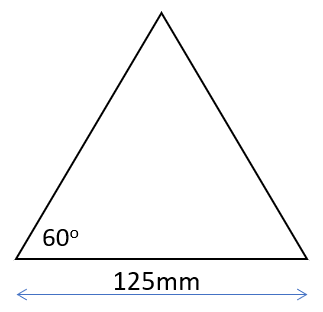
As the sides are all 125mm just slip the values into the cosine rule for angle A (it doesn't matter really which, for this particular question).
All sides are 125mm, just slip the values into the cosine rule for angle ‘a’ given:


Q2. Given angle A = 21.30 and sides ’b’ and ‘c’ as shown, evaluate the length of side ‘a’ and the remaining angles B and C.
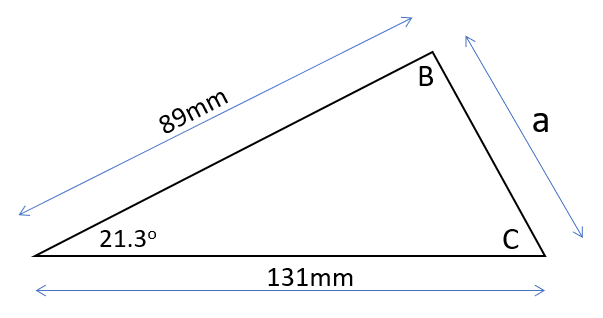
Using the COSINE RULE we can establish the side length of a:
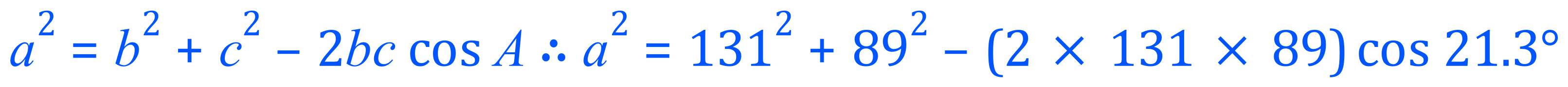
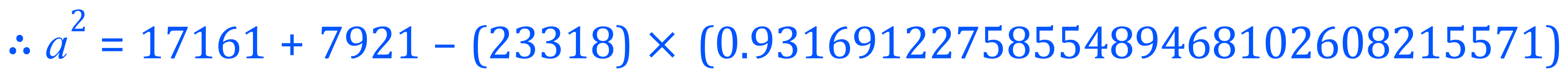

Now we know the lengths of ALL 3 sides.
Again we can use the COSINE RULE to establish either angle B or C…let’s do ‘B’
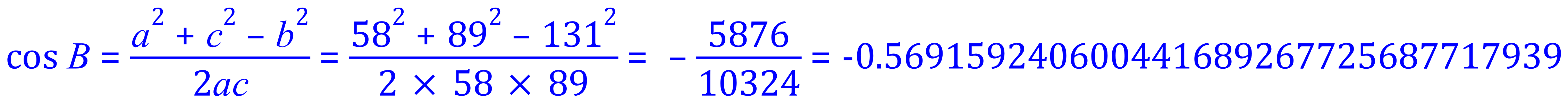
![]()
But wait……can we have a negative number for our cosine value here?, Can the cosine really be -0.569...... ?
Well as you can see, the angle that we end up with is obtuse, ie: it is between 900 and 1800 but perhaps we should look at the rules for ‘the signs of SIN COS and TAN’:

The diagram tells us that our COSINE being negative should give us an ARCCOSINE between 90o and 270o – just checking back against the triangle in the question shows that the angle is obtuse (90o < ϴ < 180o), not acute (<= 90o) or reflex (>180o).
Q3. Given the information shown, calculate:
- The area of triangle ABC
- The length of side AB using the cosine rule.

The first part of the question required a little bit of knowledge of the area of a triangle and the formulae we need to work these out. The most common formula is this one:

Where "b" is the length of the base (any selected side) and "h" is the perpendicular height. Not a lot of use here as the perpendicular height isn't easy to establish with the information given, however another rule of mathematics allows us to calculate the area of a triangle if we have the required entities to satisfy the cosine rule, ie: two sides and the angle between them.
Let side BC = a, included angle (b,c) = A
Let side AC = b, included angle (a,c) = B
Let side AB = c, included angle (a,b) = C
This is just a simplified naming convention, but the formula we need is:
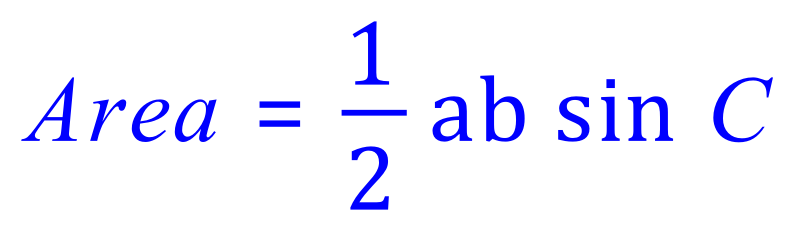
Now we can use the information we have, as the value for "a" is the length of side BC = 8.35cm and the value for "b" is the length if side AC = 7.20cm. The included angle is "C" = 74o.


Q4. Given the triangle ABC and the information shown, calculate:
- The PERIMETER of triangle ABC, quote your answer to 3 significant figures.
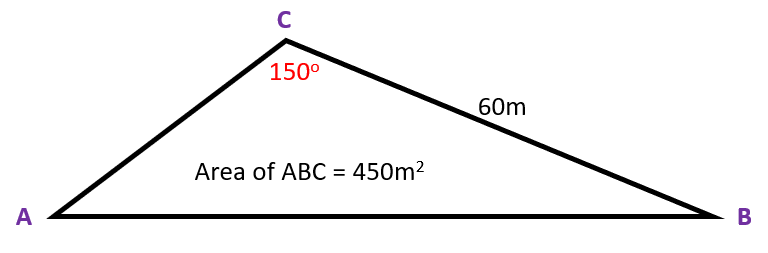
This is a question that relies on the use of the trigonometric formula for the area of a triangle and the Cosine Rule. It will be completed in stages. The Cosine Rule requires the length of two sides and the value of the included angle, so we are missing the length of side AC......this is our first task:
I am going to annotate the above triangle with the trigonometric references we will use, ie: the side labels we will find in the formula for the area, viz:
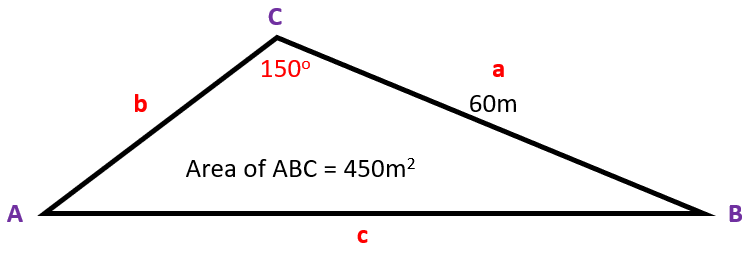
We know side "a", we need to find side "b". This requires a little bit of permutation of the formula for the area of the triangle:

We need to make "b" the subject of the equation, let's do this in steps:
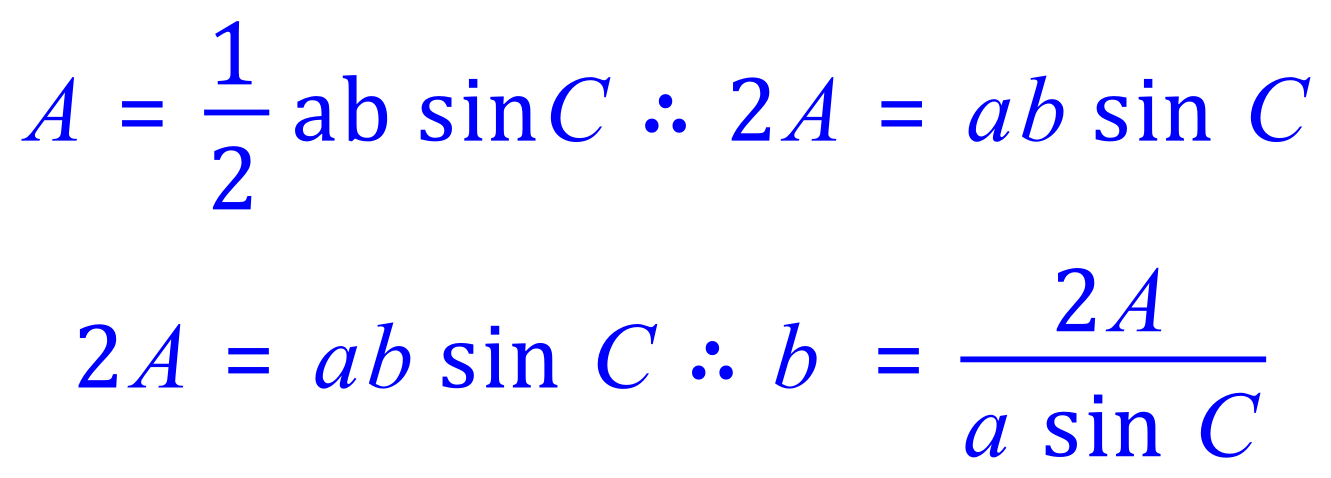
Stop here for a while and make sure that you can see where this came from.
OK..... now "plug in" the values we have been given, remember to work to FULL calculator accuracy until you reach the end, then and only then should you "round".
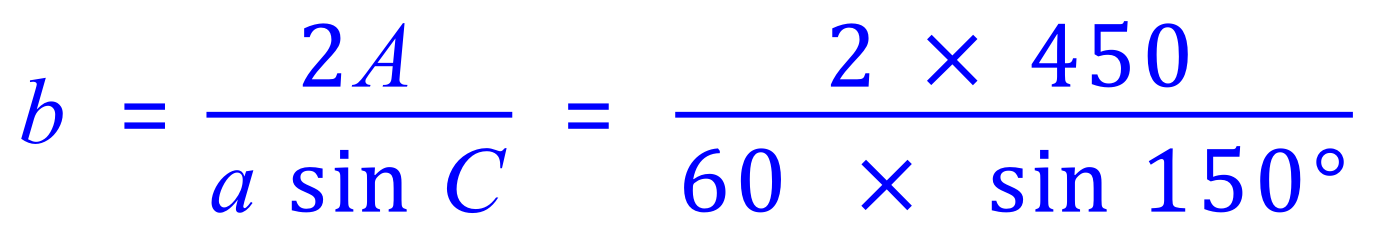
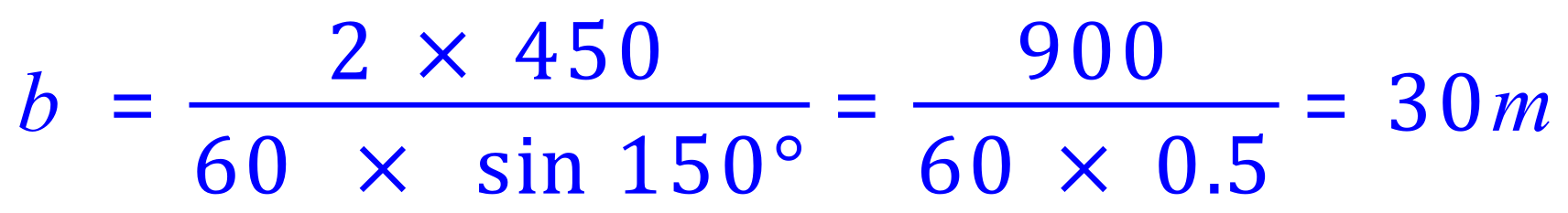
(NB: Sin is positive in the second quadrant...... see the diagram above).
NOW ...... we have the information needed to evaluate "c" using the Cosine Rule:
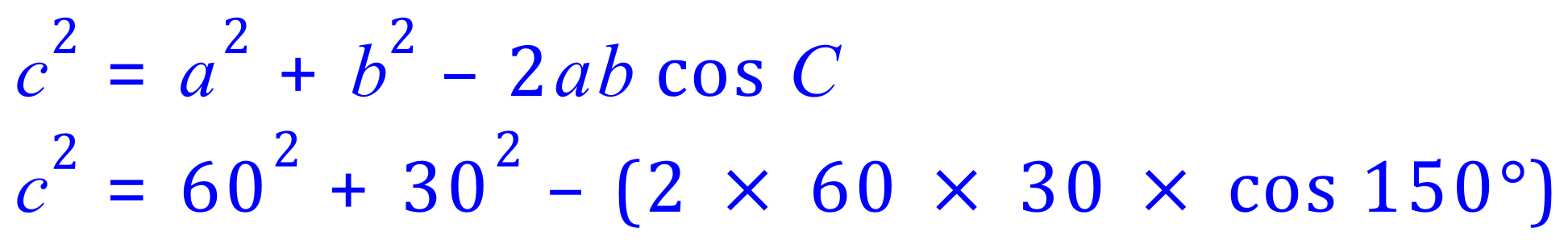
Remember ..... get into the habit of writing ALL steps down, so that anyone following your work can spot errors if they are there.

The value for "c" is therefore the square root of our final result:

The perimeter of triangle ABC is therefore:

Back to >> Questions <<
Back to >> Cosine Rule <<