Cosine Rule
The COSINE Rule
I’ll let you into a little confession, in setting the question above I simply drew a triangle on the screen and used an ‘on-screen ruler’ to work out the side lengths, but I needed to give you at least one angle or you wouldn’t have been able to do the question.
To do this I used the Cosine Rule, this is a tad more complicated than the Sine Rule, especially if you want to rearrange the terms to provide a solution to the angles, but let’s look at the formula first:
In a triangle with sides a, b and c and angles A, B and C:
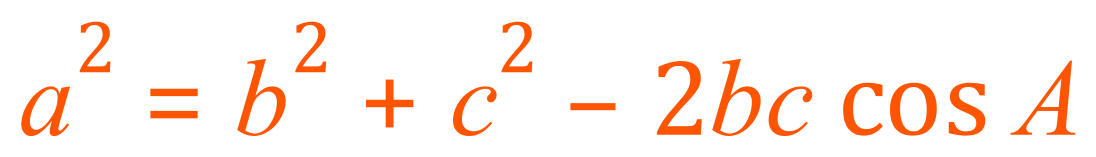
Also…..
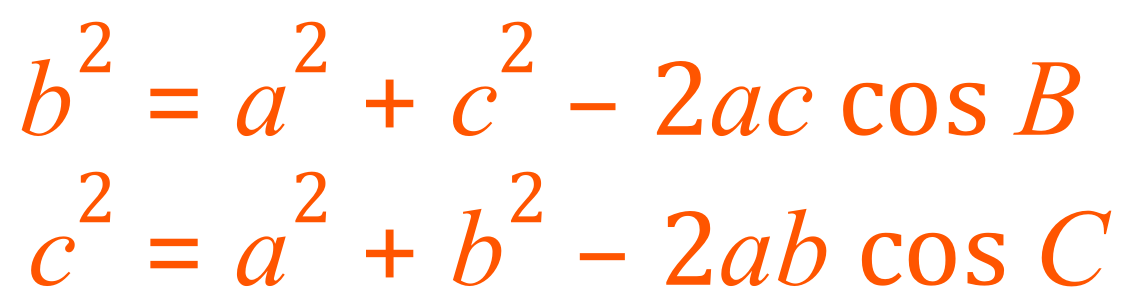
Note that the first equation in orange is the ‘main’ equation, the remaining two are just transformations of the first one.
You can probably see that the cosine rule can be used when you have:
- Two sides and an angle
- All three sides
In the latter case the equation would be ‘transformed’ (as I mentioned earlier):
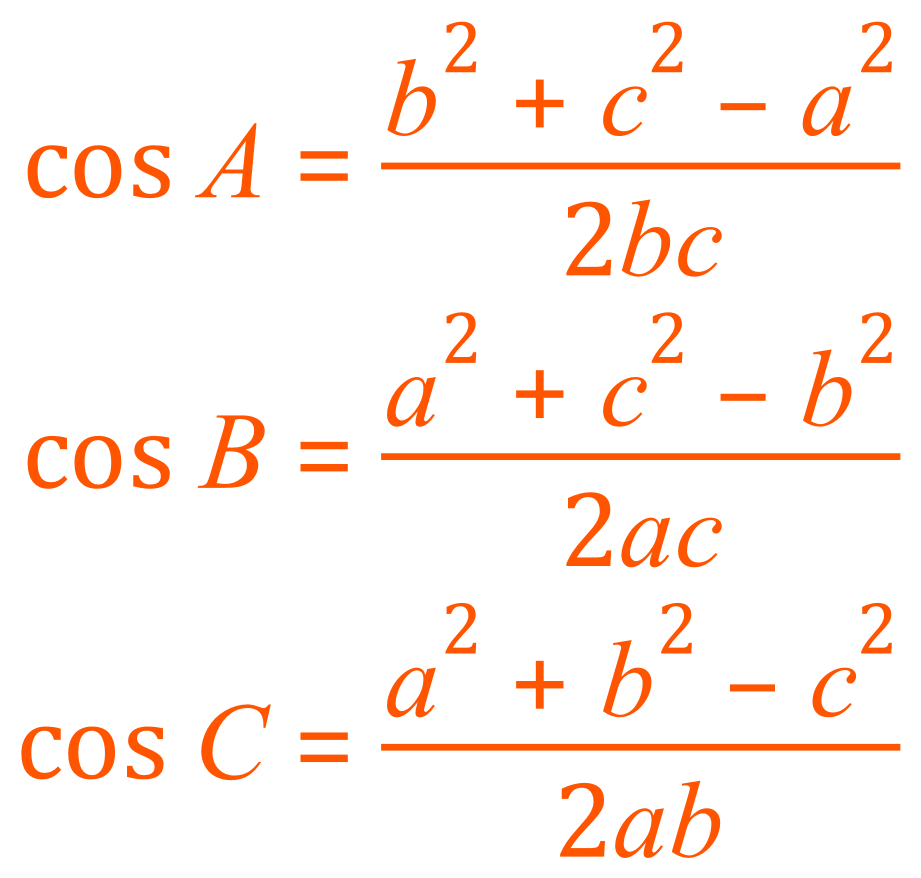
Then the inverse of the cosine function (the arccosine or cos-1) would be applied to the result to arrive at the angle.
OK…remember these……..?

Although we don’t usually need the complexity of the sine and cosine rules for right angled triangles they can be applied if you wish.
We have a standard 3-4-5 triangle and previously worked out the angles to be 900, 36.90 and by deduction 53.10 but now we are going to confirm these using the sine rule and then recalculate using the cosine rule as a little bit of practice:
First of all:
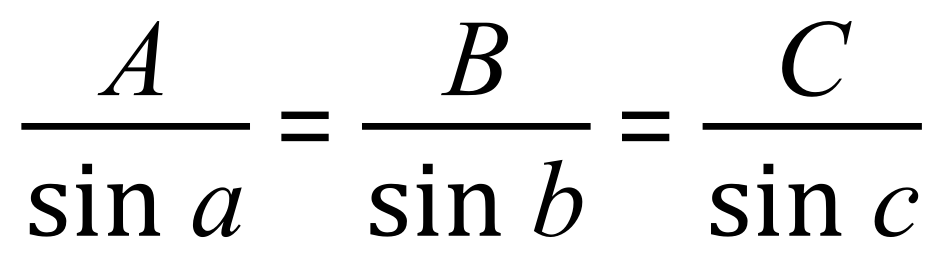
Or
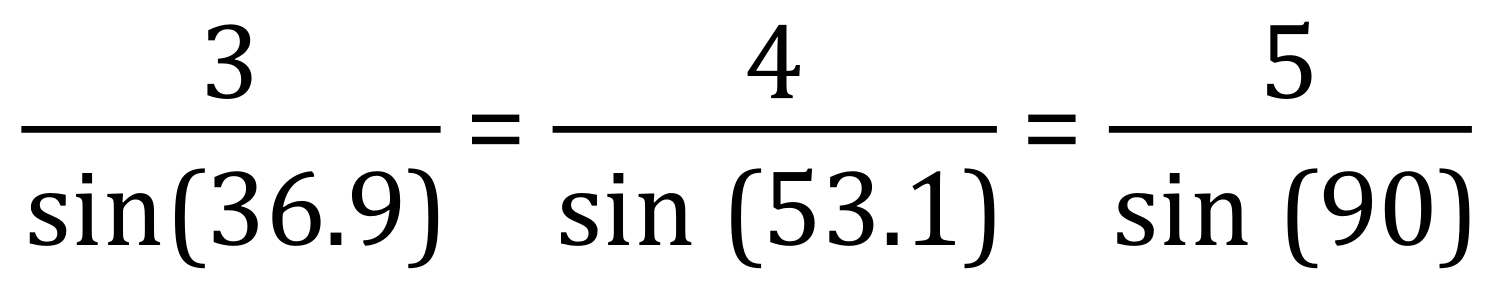
Does this work?
Well let’s see:
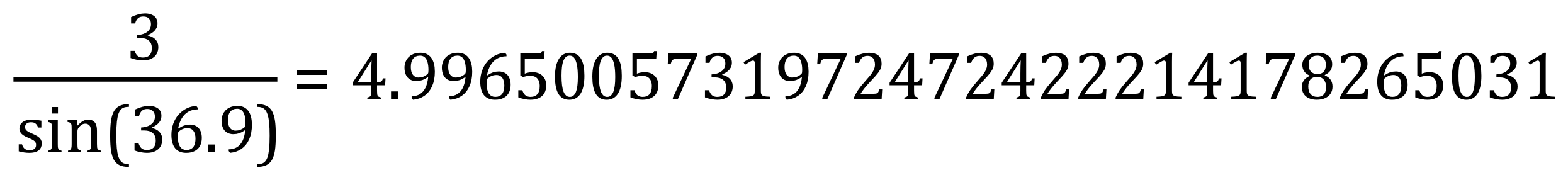
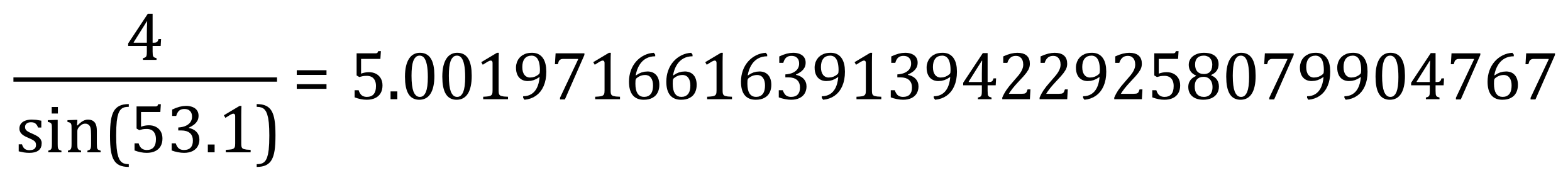
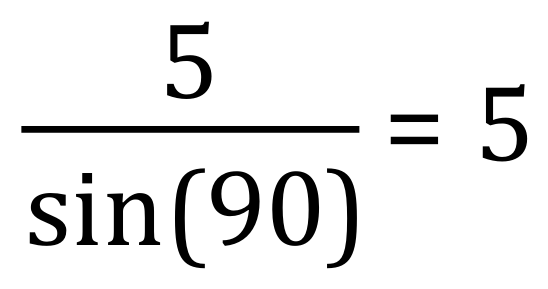
So we can see that within the limits of the numbers I have used, the answers to 2 dp would be the same, i.e.: 5 so we have validated the angles as correct.
Using the cosine rule and the sides only:
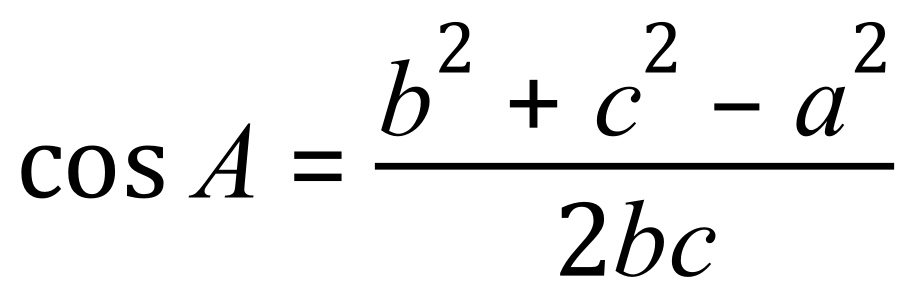
So
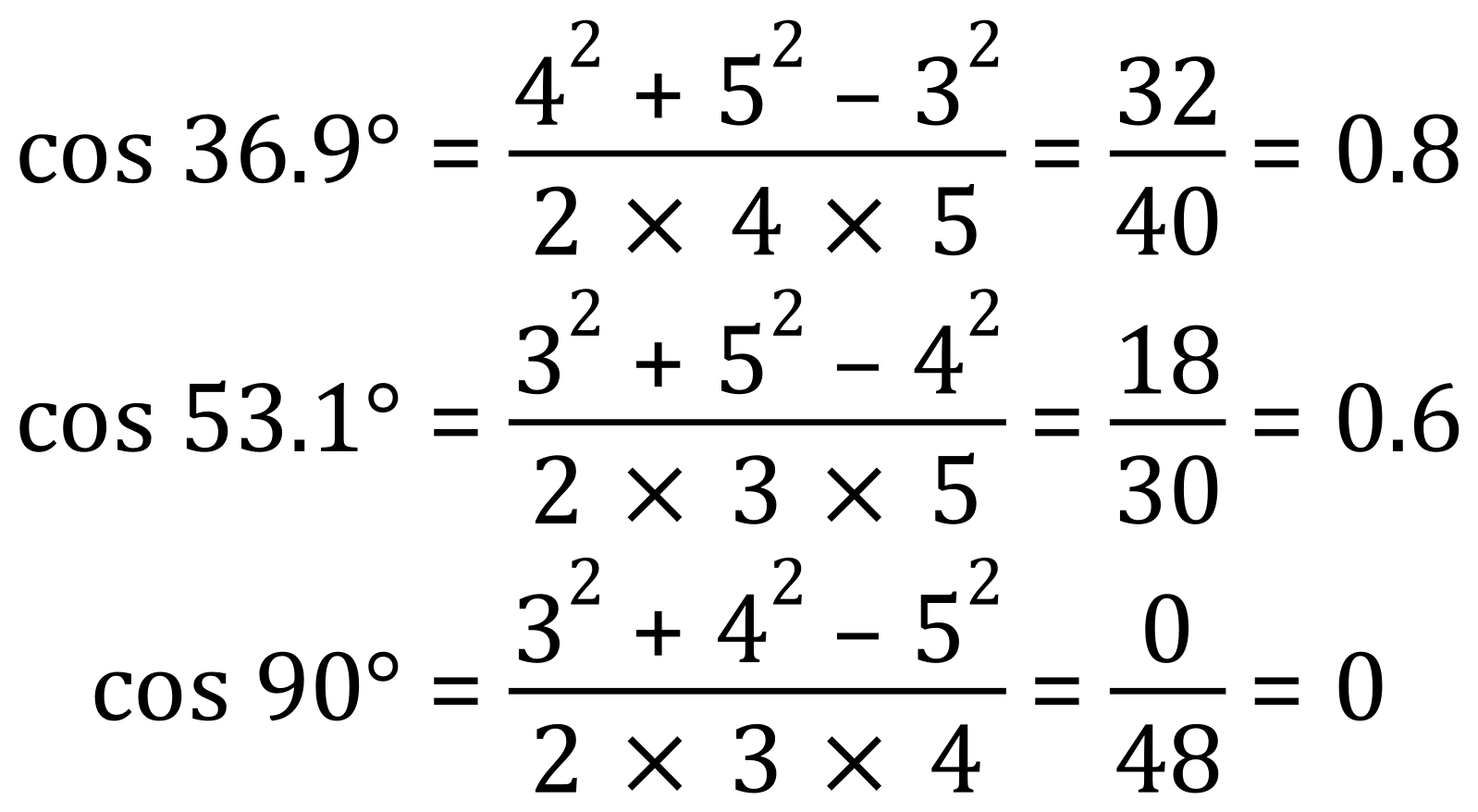
Cosine Rule >> Questions <<