Surds Rule 5
Rule 5 can probably be regarded as an extension of rule 4; it allows us to deal with more complicated “surd denominators” using the “difference of 2 squares” method:
Let us look at the rule:
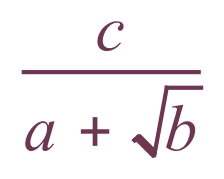
We multiply the denominator in this case by the expression:
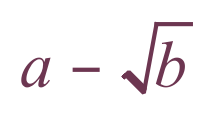
Let us see what the expression looks like before we actually carry out the multiplication:
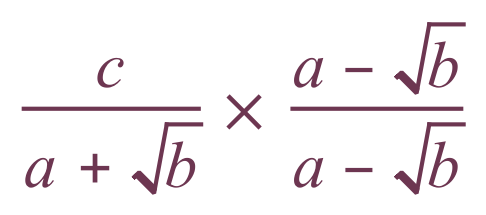
Well, you might be thinking to yourself at this point “how does this make things simpler, we are effectively multiplying our original expression by one but where is this going to take us?”
Consider this expression:
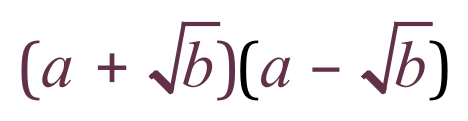
You can probably see that this is in fact the product of the denominators above, but let’s multiply it out and see what happens:
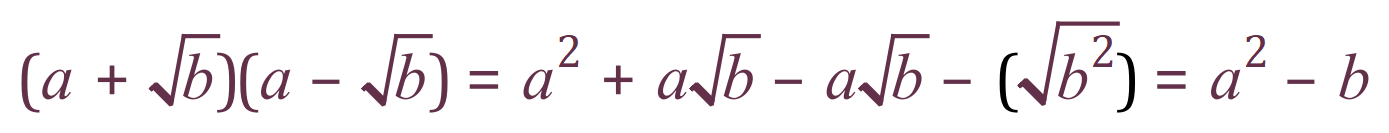
Straight away you can see that the end result is considerably simpler than what we had at the beginning, and this suggests that when we come to rationalise using this method we will indeed have got rid of the square root expressions on the denominator, leaving us with a simple integer subtraction.
This will become clearer once we have looked at an example or two, so let’s do that now:
Example 1:
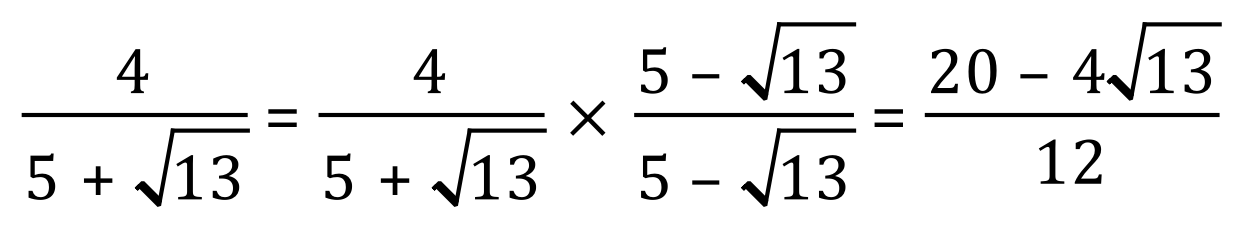
Note that a2 is 5x5=25 and of course the square of any square root returns the original number.
The above expression can be further simplified to:
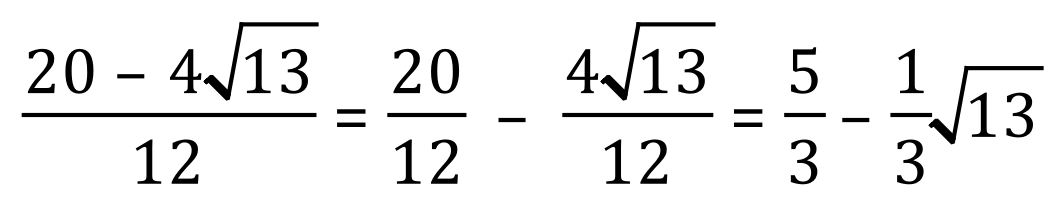
Example 2:
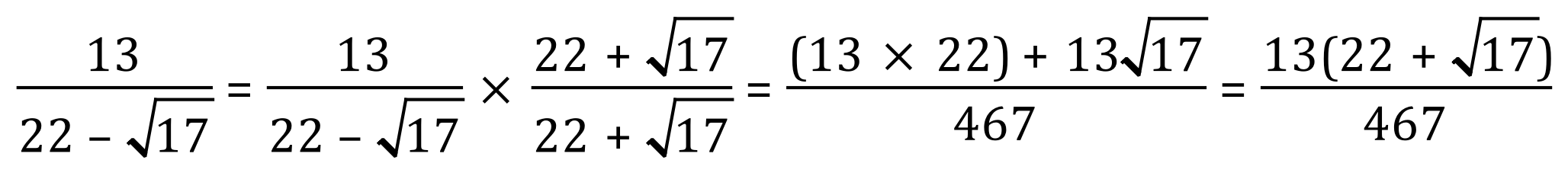
Not perhaps the best expression, it is sometimes that case that the expression you are left with is more complex than the one you started with.