The Hexagon / Sexagon
A six sided shape that is a little bit more “uniform” than the Pentagon.
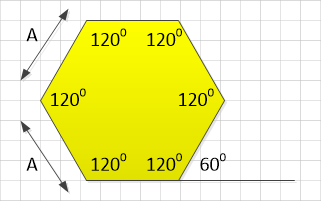
In just the same way that we added up the internal angles of the Pentagon to reach 540°, we can add up the internal angles of the hexagon and reach 720°
The sum of the external angles is once again 360° being the number of sides multiplied by the value of the external angle. This is leading us to a small formula to calculate the internal angle of any polygon which we will come to soon.
There are in fact an infinite number of regular sided polygons with seven, eight, nine… equal length sides but of course the more sides we have, the greater will be the sum of the internal angles although the external angle sum will continue to be 360°. Have a think for a moment what you think a polygon with an infinite number of sides would look like?
To help you along a little bit, take into account the fact that in all of the shapes we have seen so far as the number of sides has increased, the relative length has decreased (that is pro rata, of course we can continue to make the sides as long as we wish to by drawing each shape larger and larger each time, but if we try to keep it in proportion by drawing each shape with the same “approximate radius” the side length will appear to decrease).
As the length of the side gets smaller and smaller it will reach a point where it will be difficult if not impossible to distinguish one side from another and also to distinguish where one side ends and another one begins.
You might have cracked it by now but a polygon with an infinite number of sides is a circle.