The Triangle
The Equilateral / Equiangular Triangle
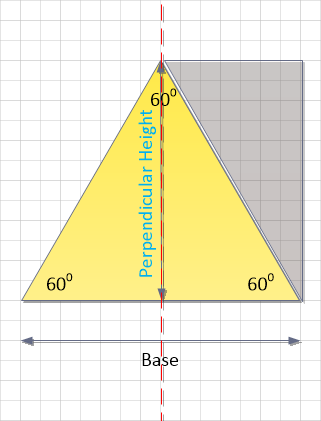
Okay then, let us now take a look at our first simple two-dimensional shape - the triangle:The example shown is that of a triangle where all sides are of the same length and all internal angles measure the same. Mathematically this is called an Equilateral triangle but could also be called an Equiangular triangle.
To measure the area of a triangle we multiply the half base value by the perpendicular height:
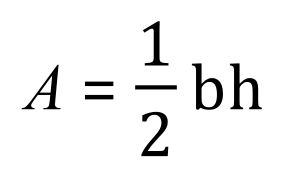
Stop and study this for a moment, if we were to cut this triangle out of paper and then cut in half down the perpendicular height we would find that the left-hand piece rotated correctly would fit over the top of the grey triangle which should help you understand why we use half of the base value but the full perpendicular height.
When the triangle is not as compliant as this, in other words the "perpendicular height" is not quite so easy to establish, there is another rule using basic trigonometry which can help, provided that we have knowledge of the lengths of two sides, and the value of the angle between them.
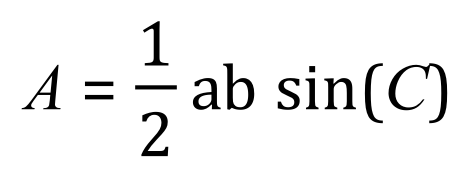
Where "a" and "b" are the lengths of the two known sides, and "C" is the value in degrees of the angle between them.
There are three different types of triangle, the Equilateral triangle as we have seen above, the Isosceles triangle which has two equal sides (and therefore two equal internal angles) and the scalene triangle which has no equal side lengths and consequently none of the internal angles are equal either.
The Isosceles Triangle
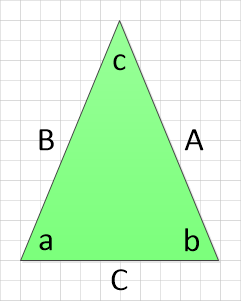
In this example, the isosceles triangle is shown. The properties of this shape are such that:
- Length of Side A= Length of Side B
- Value of Angle a = Value of Angle b
- And as with all triangles, a+b+c = 1800
Once again the same formula is used for the Area of the triangle, usually if you are asked to evaluate this you will be given sufficient information such as a side length (A or B, plus C) and an angle (a or b) from which the calculation can be made.
Refer to the section on the Sine and Cosine Rules for examples of this.
The Scalene Triangle
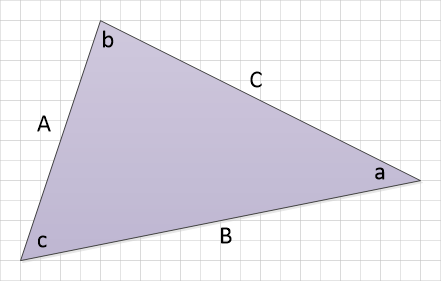
In this, the last but one of the triangles we are going to meet in this section we can see that none of the sides have the same length and consequently none of the angles of the same value, however the rules with regard to area (how to calculate it) still apply and the rules with regard to the sum of the internal angles of a triangle also still apply, that is they still add up to 180°.
It is usually the scalene triangle that we will be given an example of when we are asked to apply the sine and/or cosine rules and along with this we will be given the requisite values of the angle or side to enable us to make our calculations.
When we consider the angles, if the value of an angle is less than 90° it is considered to be an “acute” angle, when the angle is exactly 90° it is of course a “right angle” and when the angle is between 90° and 180° it is regarded as “obtuse” (we will come to these later on when we look at lines and angles in particular, and when we go into the trigonometry of triangles using the aforementioned sine and cosine rules).
I said above that this was the last but one of the triangles, the final one is in fact the “right angled triangle” or the “right triangle” which deserve special mention because it is unique and features prominently in the area of trigonometry. For that reason I’m leaving the right angled triangle to the section on trigonometry (so you need to flick there now if you wish to >> click <<).