[A] Formula for the Volume of a Cone
Consider the straightforward line graph shown below:
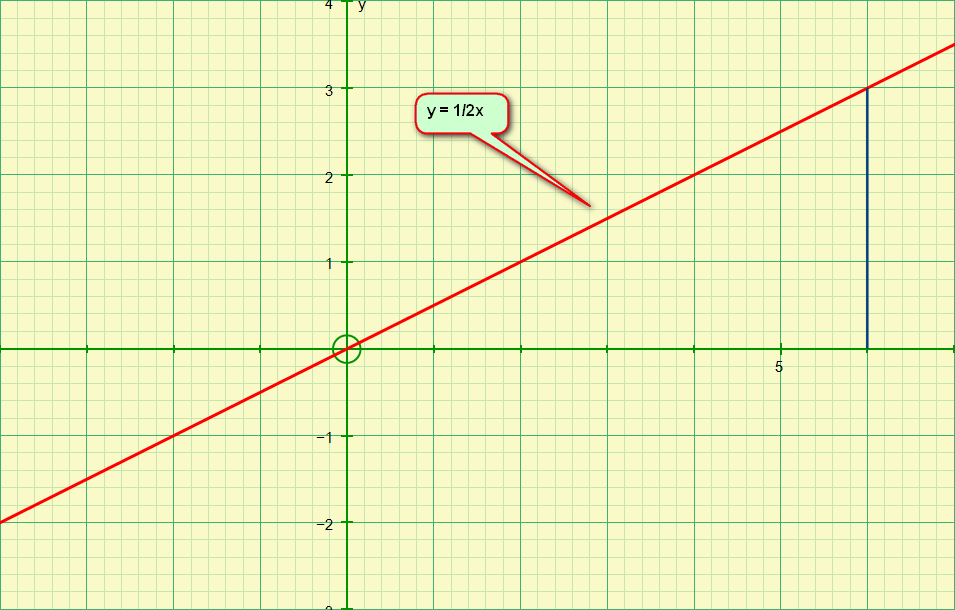
This is a simple linear plot of the function:
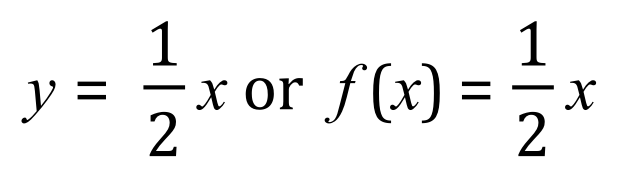
Therefore for every value of ‘y’ we have a corresponding value of ‘x’ which is half the size, and of course in the true y = mx+c fashion we have a value for ‘m’ of one half and the value for the constant of zero (so in this particular case we will disregard the constant). I have chosen in this particular example to set the limits at 6 and 0 because although I intend to calculate the volume of the solid of revolution and give you an actual numerical answer I do also want to use this particular example to show you how to establish the generic equation for the volume of a cone.
First of all let us calculate, between the limits given, the value of this particular volume of solid of revolution, shown below in the three-dimensional picture.
Step one: restate the problem:

Step two: square the function:
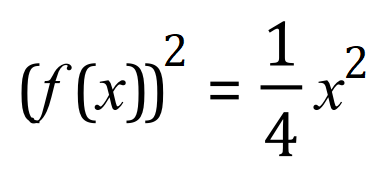
Step three: apply the formula for volumes of solids of revolution, remembering that pi is a constant and can be left outside the integral (constant multiple rule).
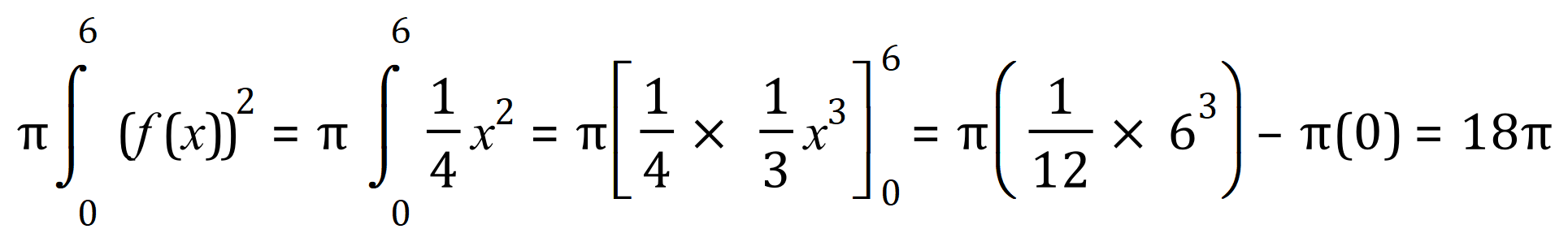
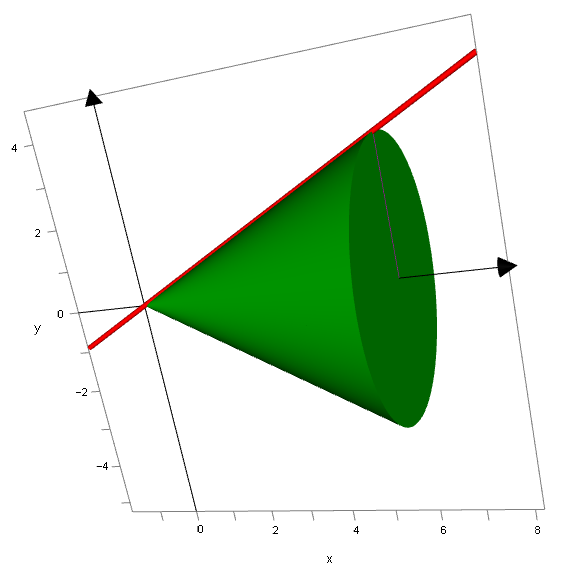

So what we done here is calculated the volume of a cone with a height of six units and the base radius of three units and if we now apply the well-known formula for the volume of a cone we can confirm that this is in fact correct:
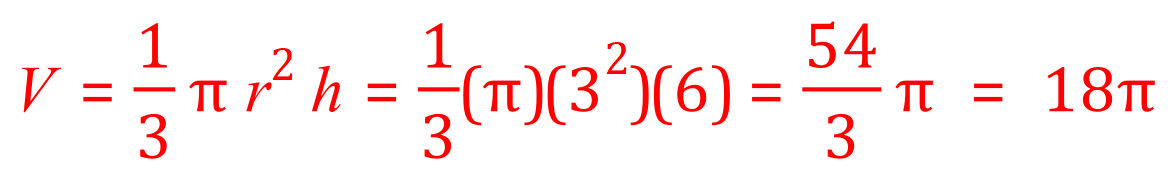
But I can hear you say “you have just given us the formula, but you said at the beginning that we were going to derive it”… Well in fact that’s what we’ll do now first of all let us go back to our two-dimensional graph of the function we started with.
As I said on the picture below the gradient of the graph is the “rise” divided by the “run”, this time we can’t call it a half because it may not be, we choose to call it simply “ ‘r’ divided by ‘h’”
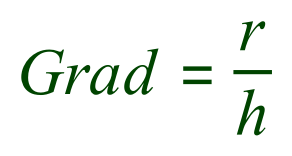
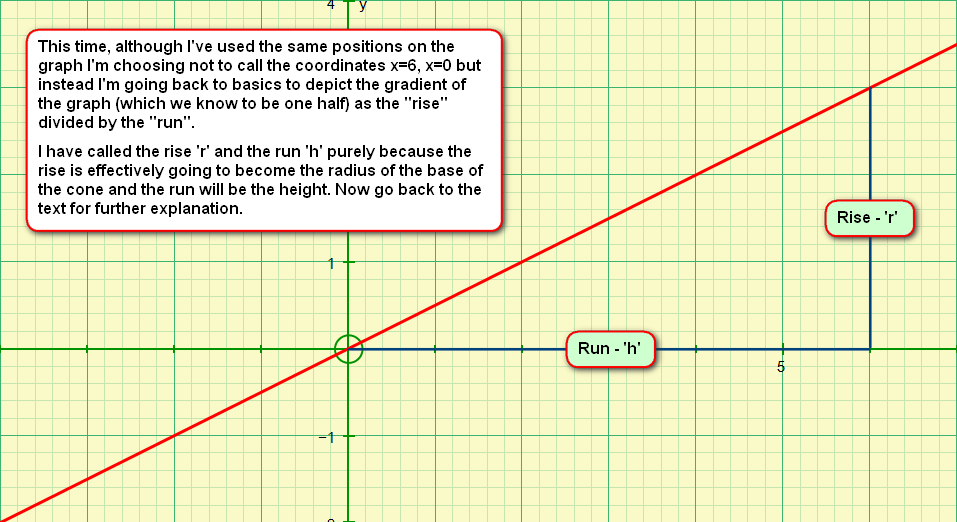
Therefore our function becomes:
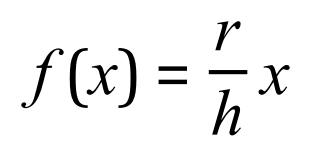
What we do now is follow the rules for volumes of solids of revolution and square the function ready for its integration and subsequent multiplication by pi.
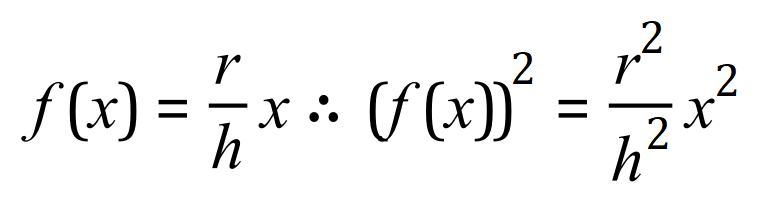
And using the standard formula for VOSOR:
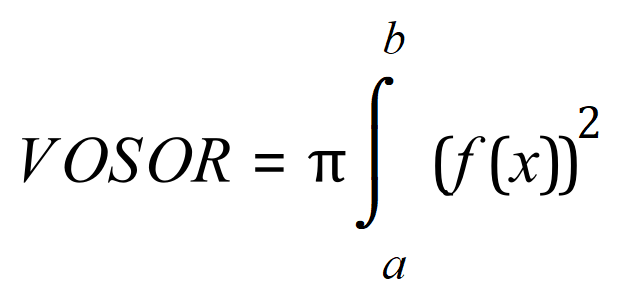
We arrive at the following expression:

Pause for a moment to study this. ‘r’ and ‘h’ as well as pi are constants, so we can rearrange this to enable us to integrate on ‘x’:
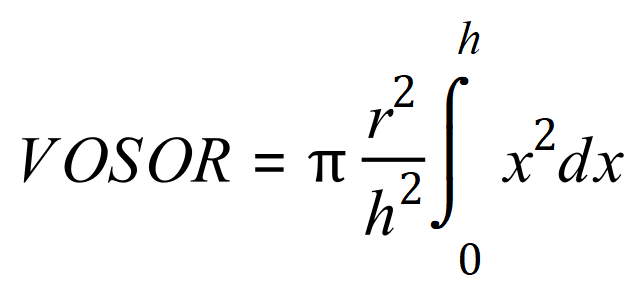
If we now perform the integration we end up with this:
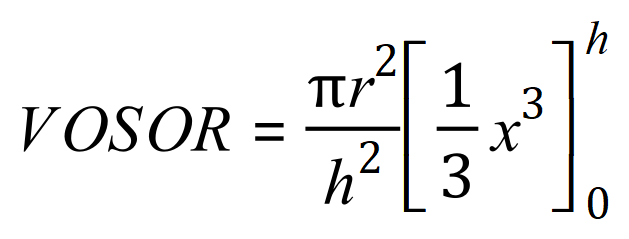
and if we now substitute ‘h’ for the variable ‘x’:
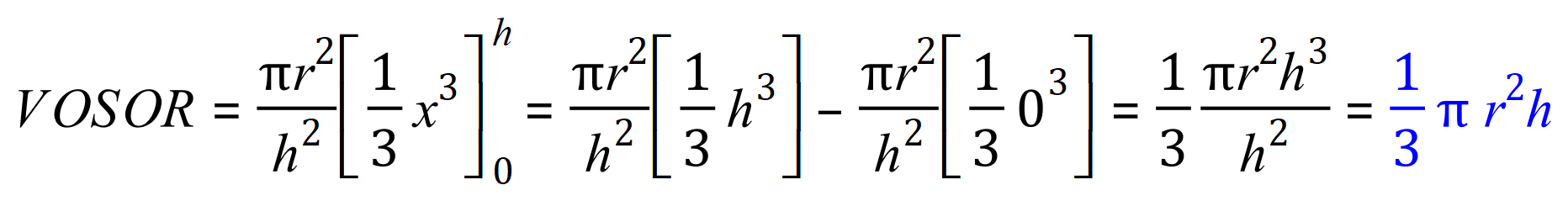
you might need to study the last equation for some time, but using the limit of ‘h’ we arrive at a ‘h cubed’ expression which cancels down to a simple ‘h’ leaving us with the well-known formula for the volume of a cone.