In another section of the book we will talk about circles, although they seem quite a simple geometric shape there is some quite intricate and indeed complicated mathematics involved. 


The formula, or function, of a circle for the moment you will have to just trust me on when I give it as follows:



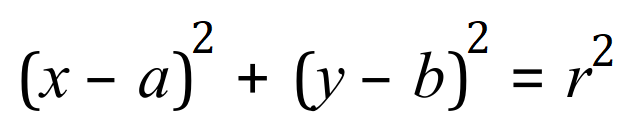
Where ‘r’ of course is the radius of the circle and ‘a’ and ‘b’ are the coordinates of the origin. If ‘a’ and ‘b’ are both zero then the formula simplifies to this:



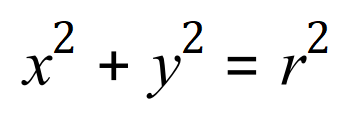
From which, by a little bit of rearrangement (which, I’m hoping you’re getting pretty good at by now) gives us an expression for ‘y’ as follows:



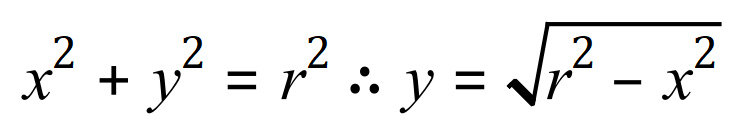
So now that we have an expression for ‘y’ let us set about working out a formula for the volume of the solid of revolution which will give us our sphere.


Step one: as is always the case by now, step one, restate the problem:



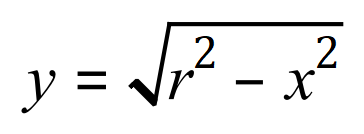
Step two: square the function ready for the integration and multiplication by pi as in all volumes of solids of revolution problems:



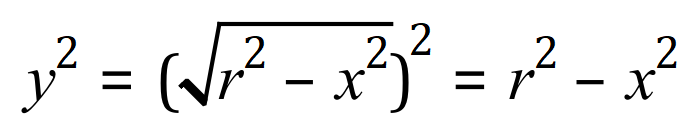
Step three: state VOSOR:



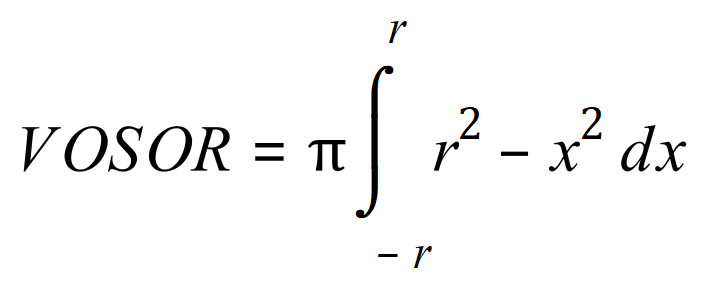
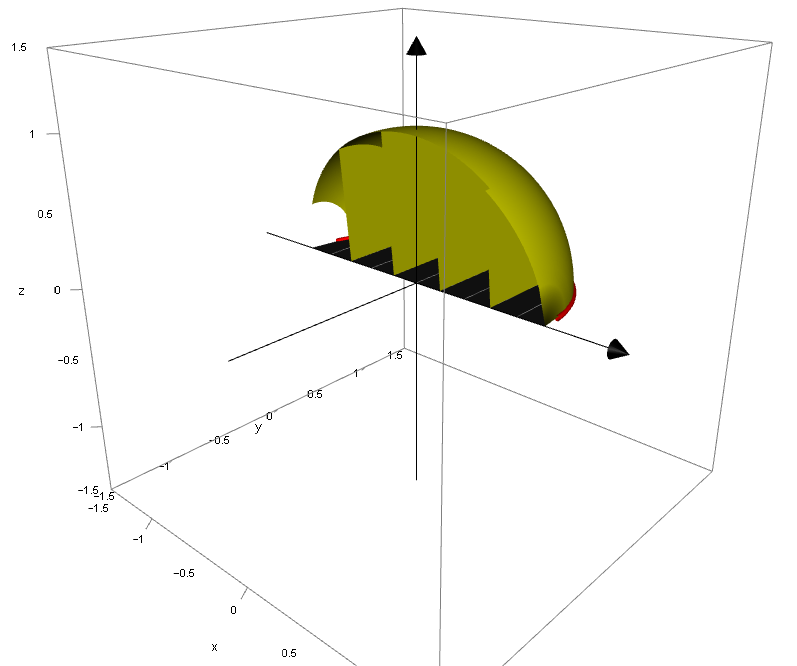
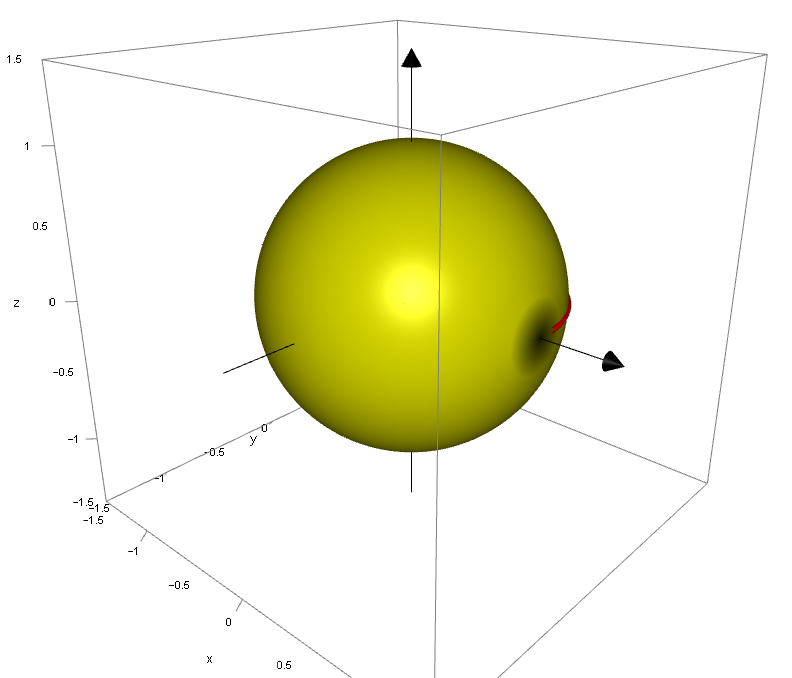
The picture on the left shows our volume of solid of revolution in the formative stages, i.e. after approximately one quarter of a turn. If you look closely towards the x-axis you can see 
a small amount of the red semicircle which formed the two-dimensional curve being rotated. The picture on the right is the completed sphere after a full rotation of 360° or 2 radians.



Step four: integrate the function w.r.t. ‘x’:



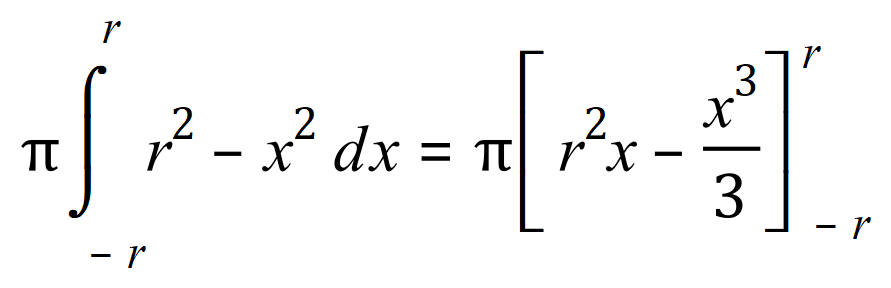
Step five : substitute values for the limits, ‘x’ = ‘r’ and ‘x’ = ‘-r’



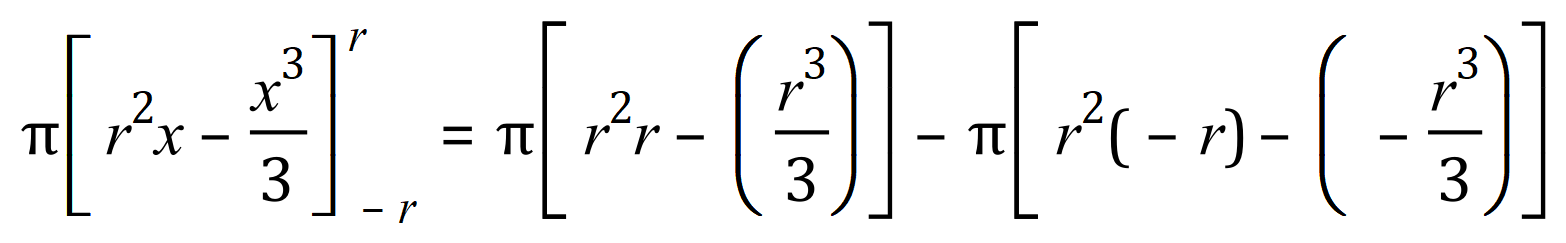
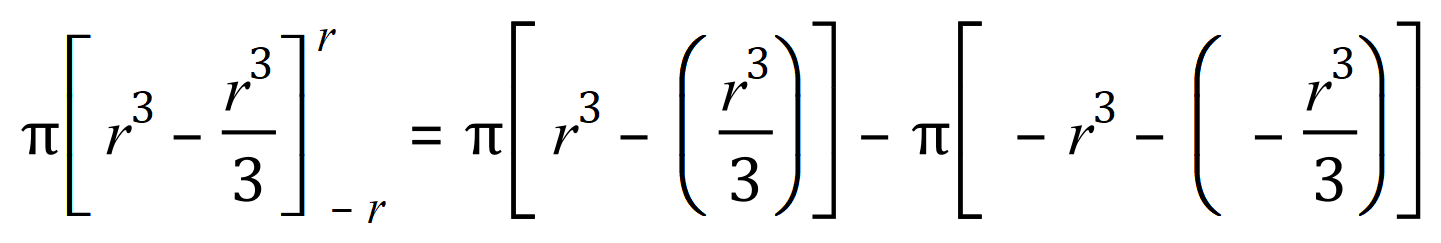
Step six: tidy up a bit:



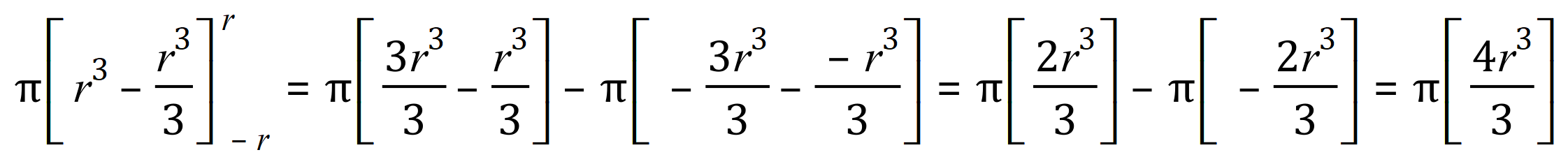
Rearranging:



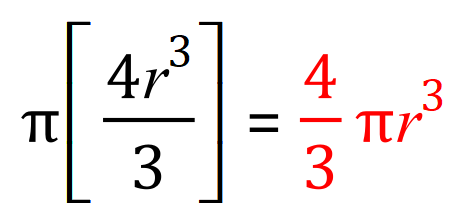
And I’m sure you’ll recall that the end result is indeed the well-known formula for the volume of a sphere.