[A] Volumes of Solids of Revolution
Just for the sake of simplicity, let’s take a look at our graph from the previous section and then later on we will look at a few simpler ones (because this one is going to get nasty!).
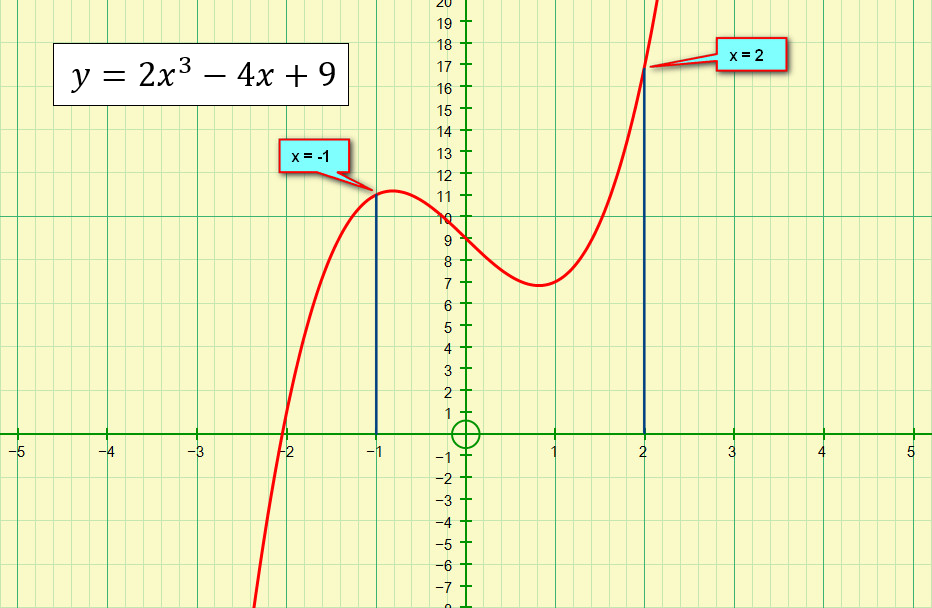
We have our function:
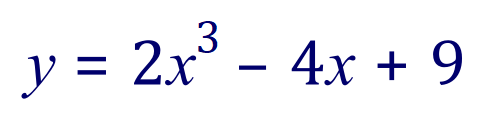
But of course now we need to know how to calculate the volume of the solid of revolution, the “formula” for this is to:
- square the function
- integrate
- evaluate between the limits set
- multiply the result by pi.
In other words:

Where of course ’upper’ and ‘lower’ are the limits of integration and “y squared” is the square of our function.
Step one: square the function…
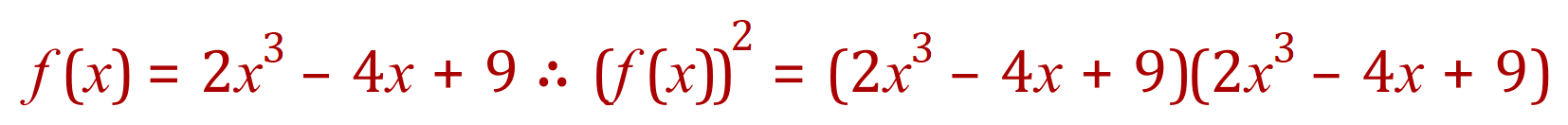
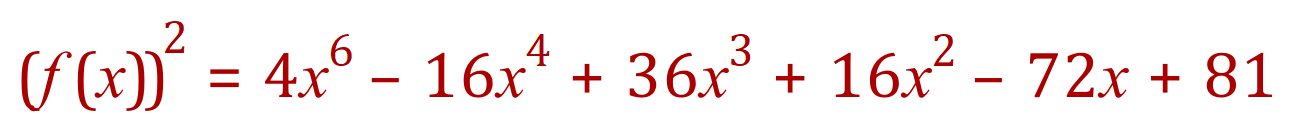
Step two: integrate the function w.r.t. ‘x’:
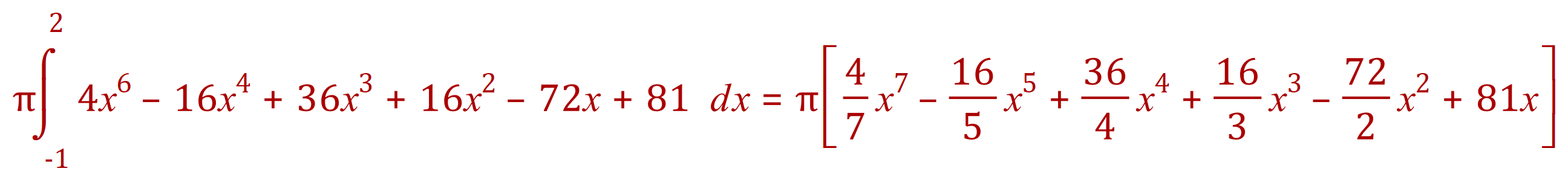
Some of the fractions could be simplified but it sometimes helps in any 'back tracing' if you have slipped up somewhere to leave them 'as is' for the time being.
Step three: Insert the upper limit value for ‘x’, obtain a numerical result:
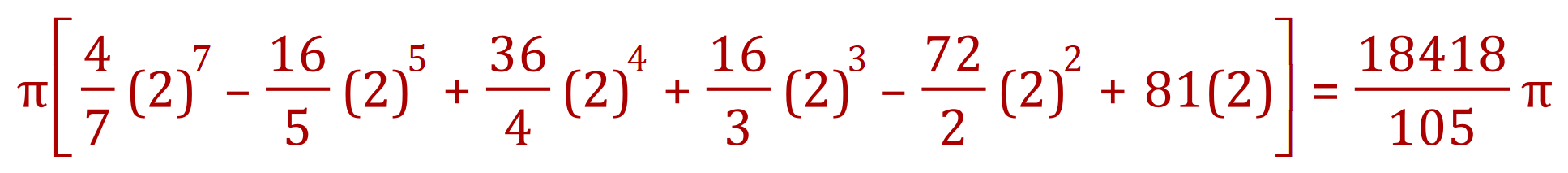
Step four: It may help to convert all fractions to the common denominator (105), as you will be leaving the final result as an improper fraction:
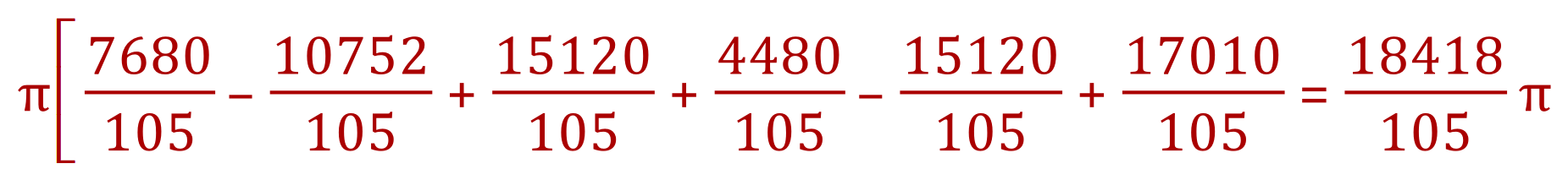
Step five: As per step 3 for the lower limit:
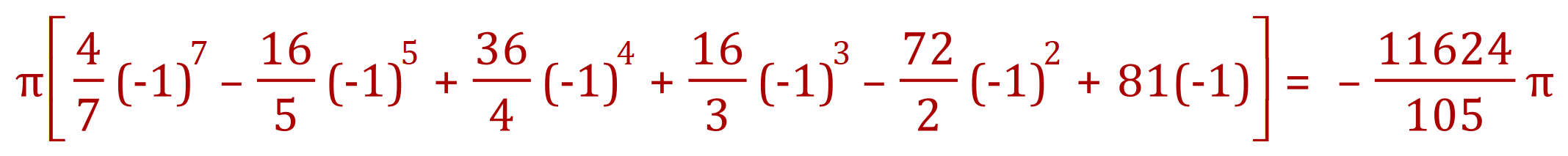
Step six: Subtract the result from step four from the result of step 3 and multiply by pi:
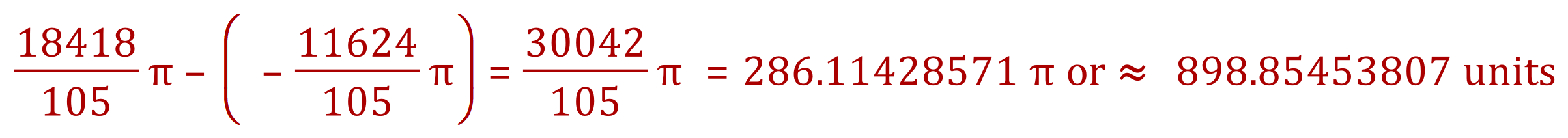
This is the final result to one decimal place, approximately 899 cubic units (depending of course on the unit you chose in the measurements, usually it would be cubic centimetres but of course it could be anything!).

The three-dimensional diagram shows the volume of this solid of revolution actually plotted out and as you can see it would make a very attractive vase! Of course this particular example was quite complicated, probably not the ideal example to use to introduce you to Volumes of Solids of Revolution.
We will now look at some significantly simpler cases. At the moment we will concentrate on definite integrals, that is given a function and a set of limits we will calculate the volume of the solid of revolution as traced out by the function around one of the axes (I say this because you can in fact to trace out a volume around the y-axis but generally speaking it seems to be accepted practice to do it on the x-axis).
Consider this function:
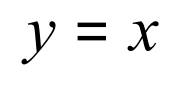
This is perhaps the simplest linear function that I can think of and when plotted will give a line at 45° passing through the origin with a positive slope, that is from the quadrant holding positive values of ‘x’ and ‘y’ through the origin into the quadrant where all values of ‘x’ and ‘y’ are negative:
Let us take a look at this very simple graph:
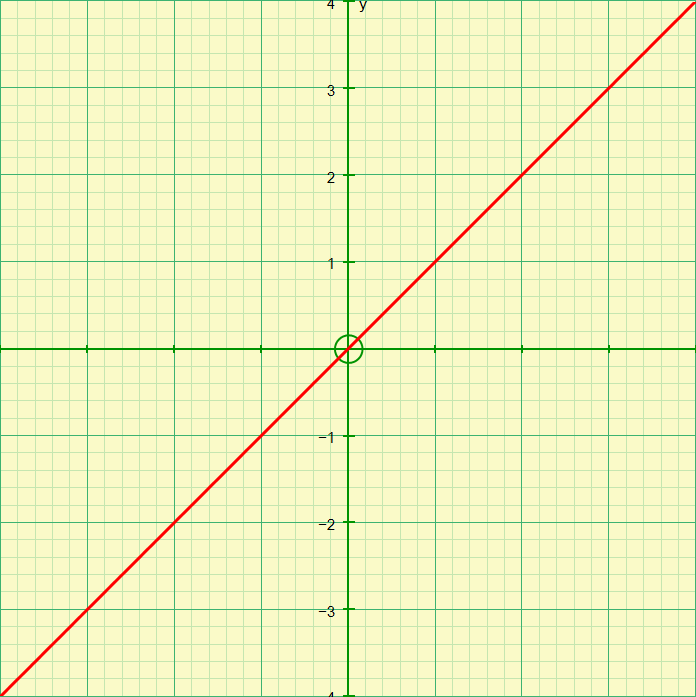
As you would expect a 45° line where each value on the line represents a value of ‘x’ with an identical value of ‘y’. What shape would we end up with if we were to trace out a volume of solid of revolution on this line?
First of all remember the rule for calculating volumes of solids of revolution:

With this in mind we will set our values for our limits of 3 upper and 1 lower.
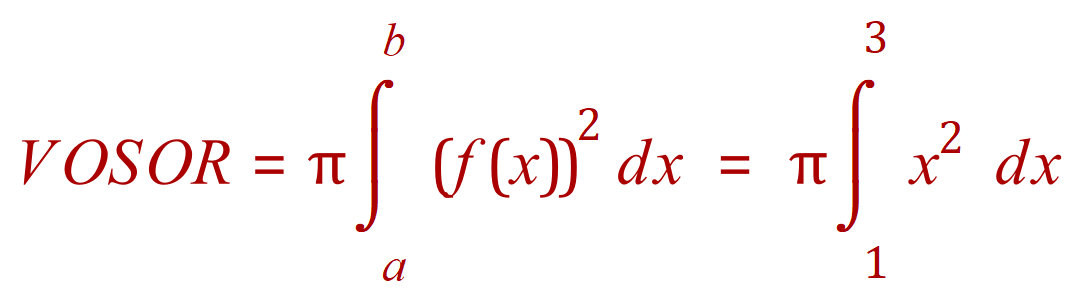
(You’ve probably worked it out but bear in mind that VOSOR is just my abbreviation for volume of solids of revolution, it’s a bit of a nightmare to keep typing this out :-) This time round I’m going to actually give you the traced out volume as a picture, and then performing calculation giving the numerical value for this volume.
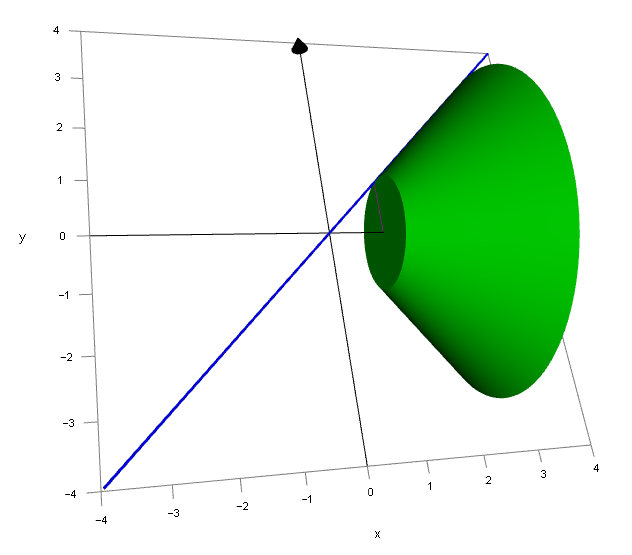
This time, to make it look a little bit clearer I have chosen to show you the volume of this particular solids of revolution from another angle, you can see that it is effectively a cone with a smaller cone sliced off the top (that smaller cone would have been traced out had I extended the lower limit to zero rather than one). Alternatively you may be able to see a green light bulb shade! In any event let us assume that this is in fact solid as the section would suggest and now calculate, using our known method, the volume.
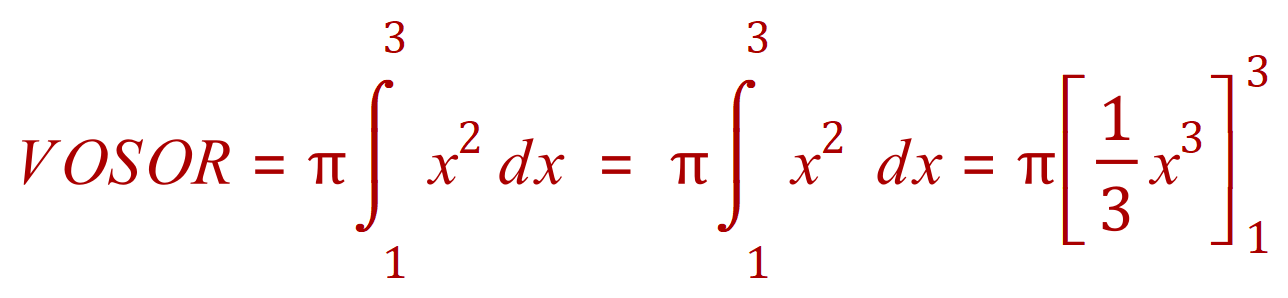
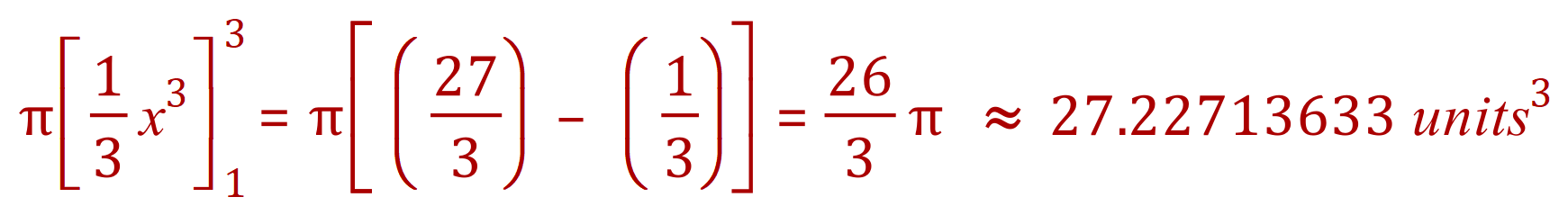
(In)Definite Integration For VOSOR Generic Formulae
In this closing section on Integration I will use a definite integral with variables instead of fixed constant values to show how certain widely accepted formulae came into being. There are many to choose from (sphere, cylinder, cone) but I will choose the first and last ones they are a little tricky but will be useful for you to work through and manipulate.
>> Questions <<