[A] Multiplication Of Complex Numbers
Multiplication of two complex numbers isn't much more difficult than the addition. It requires a similar type of operation to the 'FOIL' method used to expand brackets in algebra (first, outer, inner, last).
Algebraically:


The same approach is used with the multiplication of complex numbers, but there is a small caveat at the end of the evaluation:
Example:
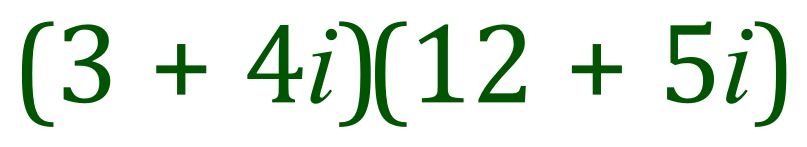
Using the FOIL method as shown above:

The final expression (the 'L' in FOIL) gives us a quadratic expression. At this point we need to remember that at the heart of complex algebra is the entity 'i' which is defined as the square root of -1.
This being the case, then if we square 'i' we arrive at -1. 20 times -1 is of course -20 so this final expression must be changed:
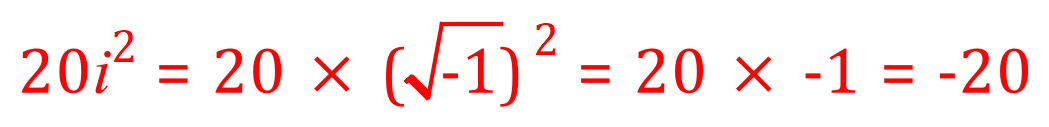
The last line of our evaluation should therefore be rewritten:

And this is the final result to our multiplication of the pair of complex numbers.
The general rule for the multiplication of two complex numbers is:
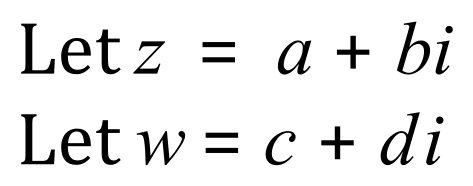



You may have noticed that when we used the FOIL method, in our generalised example when we come to multiply the inner pair 'c' and 'bi' we should effectively write down 'cbi' as the entity 'i' belongs to the entity 'b'. However, it is permissible to change 'cbi' to 'bci' as it appears to be an algebraic tradition to put variables in alphabetical order where possible and multiplication is commutative anyway so the order in multiplication (and don't forget addition) is not crucial.
>> Questions <<