[A] Division Of Complex Numbers
Division of complex numbers is probably the hardest of the four operations, take for example the following statement, there is no obvious way to complete this:

Let us step back into the world of real numbers just momentarily. Take the following two simple integers:

You are now probably thinking to yourself "but that's not an integer, that's a fraction?" But I want you to look at the two numbers which form the fraction, that is the two numbers which form the numerator (3) and the denominator (4) separated by the vinculum (that's the line that separates top from bottom).Can you think of any way that we can do this division without actually dividing? It seems that in mathematics multiplication is always (or it seems that way) easier to perform than division so if we could perform this division by multiplication (??) Would this make our life any simpler?
Think about it, "3/4 is actually 3×1/4" so what about if we split up the fraction like this and turn it into a multiplication problem?
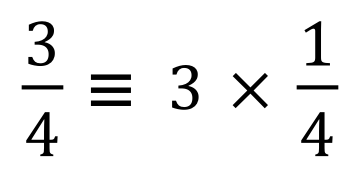
What you've actually done is taken the reciprocal of the integer forming the denominator and then carry out a multiplication, you end up with the same result either way. So we could say that to perform a division, we could take the reciprocal of the divisor (4) and multiply this by the dividend (3).
This actually forms the basis of how we perform divisions using complex numbers. For any real number (non-zero) there is a corresponding reciprocal such that the following equality is satisfied:
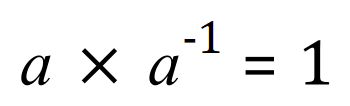
Since:
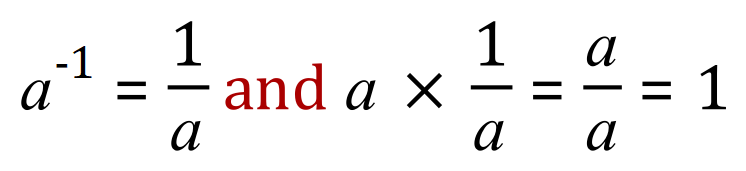
We can therefore show the reciprocal of a complex number like this:
![]()
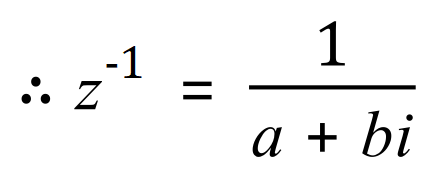
We multiply the top and bottom of the right-hand side of the equality by an entity called the "complex conjugate":
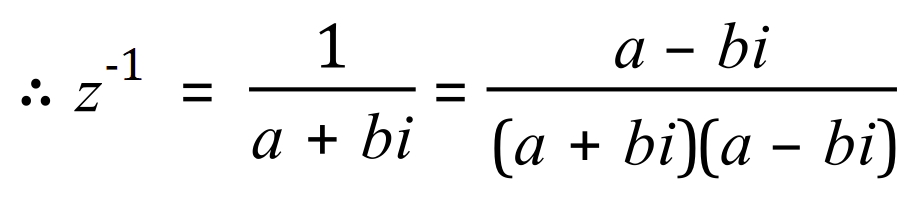
And if we now multiply out the bottom part, we arrive at the following expression:
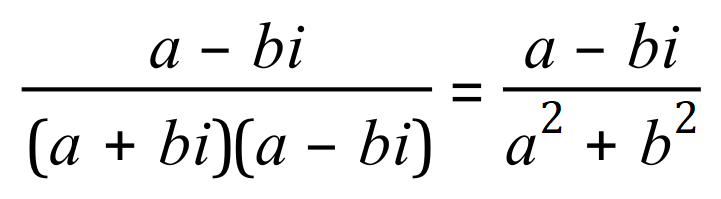
Finally:
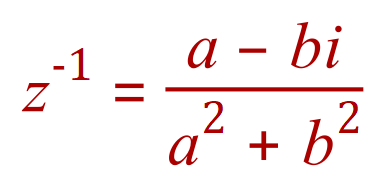
>> Questions <<