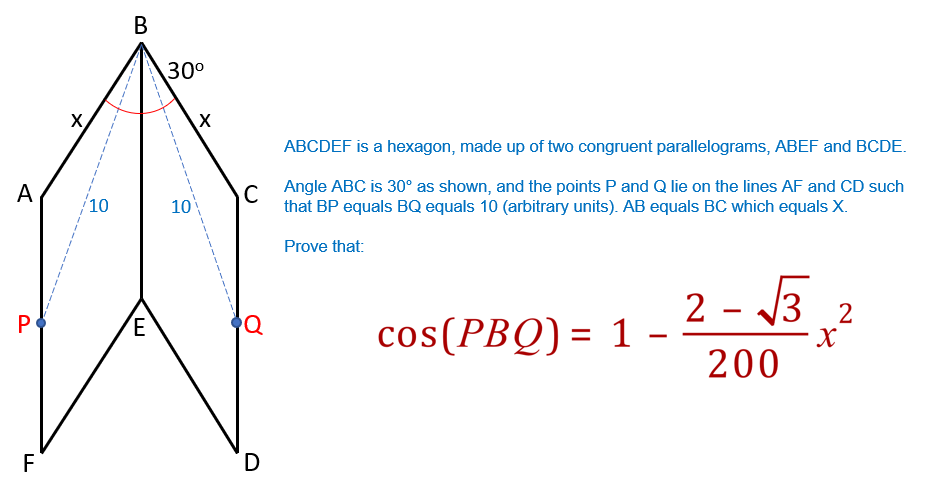
We need to work out the value of PQ as the "cosine rule" allows the evaluation of a missing angle (in this case PBQ) if we have all three sides. The congruency of the parallelograms informs us that PQ=AC so if we evaluate AC, we automatically have PQ.


Given AB = x, BC = x we can use the cosine rule to start to work on a value for AC:


Generally:

Let us take AC = a



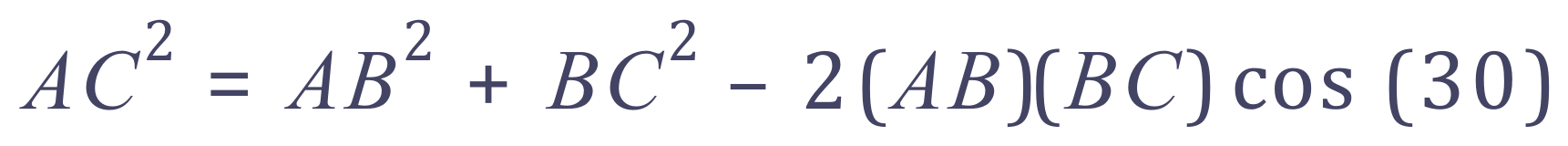
Now given the information we have, that  AB = BC = x we can rewrite the above:



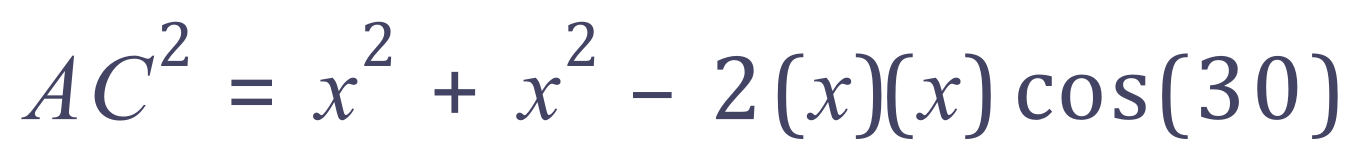
Although not given in the question, the appearance of surds in the solution suggests that we will be needing a surd representation for cos (30) as opposed to a normal decimal number. The surd representation for cos(30) is:

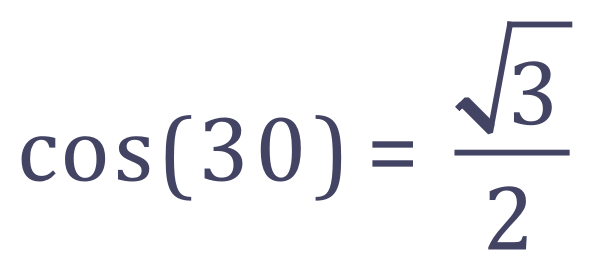
Therefore:



We now have a value for AC2 which by definition is also the value which we require for PQ2 to attempt part two of the problem. 



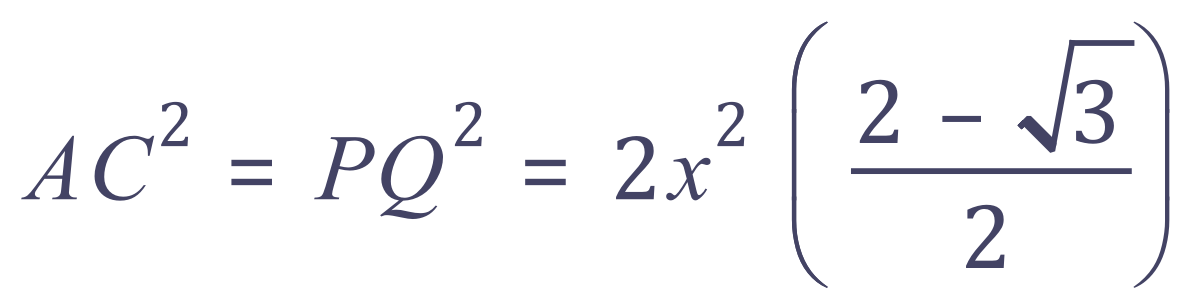
Let us now look at another triangle, the triangle BPQ, we know the following values: BP = BQ = 10, and AC2 is the result of the first part, as shown above.


Using the cosine rule again, we now need to establish a value for the angle shown in blue dotted lines, the angle PBQ. Now we know the general "formula" for the cosine rule as:


So:


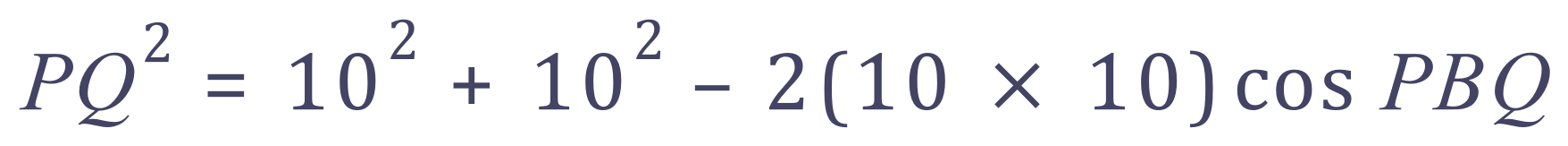
And given the fact that PQ2 = AC2:



First of all let’s tidy up the left-hand side and the right-hand side of the above equation, to get rid of the fraction and to factorise the right-hand side:



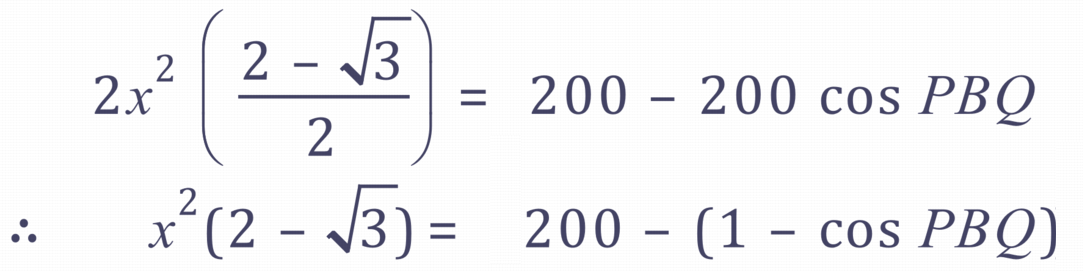
Rearranging:



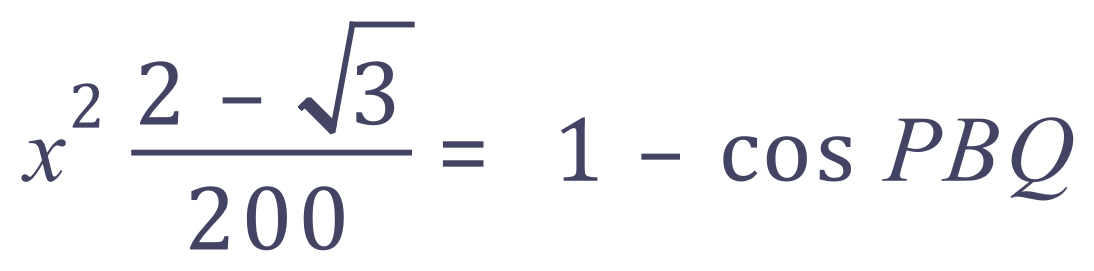
More rearrangement and multiplication by -1 :


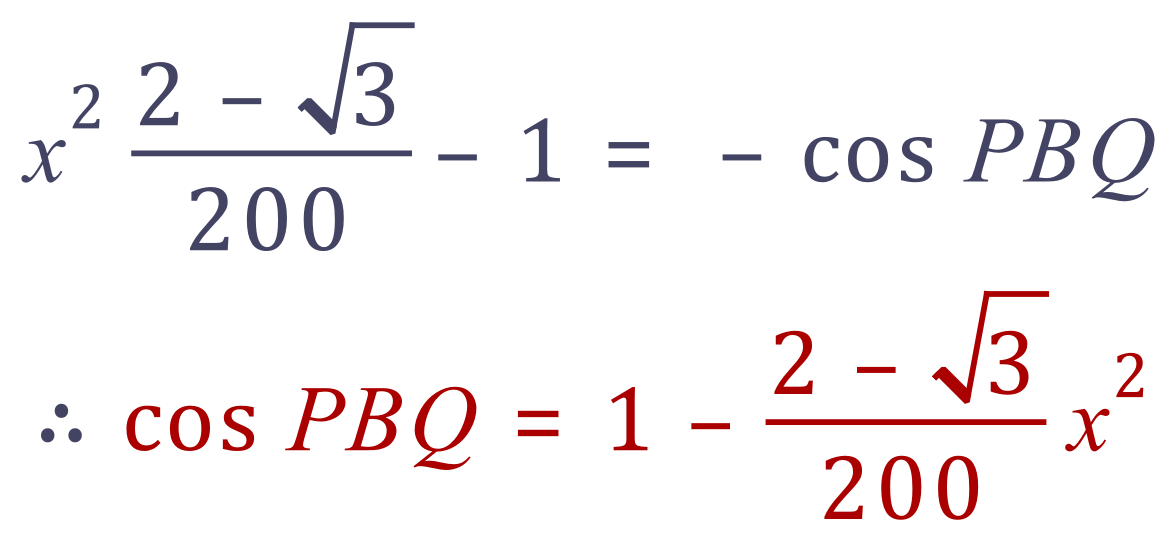
Back To >> Question <<