Hannah's Sweets
Q. There are “n” sweets in a bag. 6 of the sweets are orange and the rest of them are yellow. Hannah takes one sweet at random from the bag and eats it. Hannah then takes another sweet from the bag and eats that one too. If the probability that Hannah eats two orange sweets is 1/3, show that:
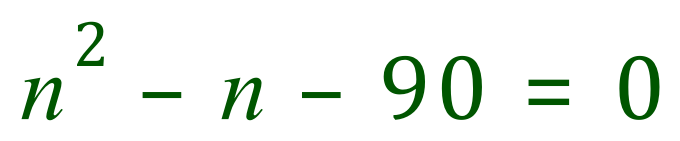
A. This question appeared on a UK Maths GCSE paper in 2015 and was also the subject of complaints from many students. Not so much the question as the “probability” in it would have been covered in the curriculum, I think it was the seemingly disjointed nature of the question that caused the confusion.
I think that the part of the question which caused the most confusion was that it initially looks like a probability question but at the very end you are given a quadratic equation! What you are not asked to do is solve the equation for ‘n’ but this could be a trap that most people would fall into, after all when you are given a quadratic it is usual to try to find the roots of it.
A good understanding of the rules of probability is essential here, not only for the obvious reason (to get the marks) but to be able to start the question at all you have to be able to see that the question is almost entirely probability.
Let us suppose that we have five balls, red white blue yellow and green. What would be the probability of selecting the green ball?
We know that probability is defined as:

Where Pe is the overall probability of the event, Pd is the probability of the outcome that you want and Pa is the probability of any possible outcome. Taking our problem of the "coloured balls", we can see that we have five in total, consisting of one of each colour. Assuming that they are in a bag, hidden and the ball is drawn out "blind" there is an equal probability of drawing out any of the balls. So the probability of the event Pe is the probability of drawing out the green ball divided the probability of drawing out any ball Pa.

In other words the probability of selecting the green ball is one divided by the number of possible outcomes which of course is five. Therefore the probability of drawing out the green ball is one in five or 1/5.
The point that I am trying to reinforce here is that generally in probability questions we are given fixed numbers, i.e. “a bag contains twelve” or “a box contains twenty-five” and in the above example, 5 balls but in Hannah's case we are not told exactly how many sweets are in the bag, in this case we are told simply that there are “n” which could of course be any amount.
(We are told that six of the sweets are orange and we can then deduce from that that the remainder (which we are told are yellow) is therefore n - 6 although this little bit of information turns out to be unnecessary).
So......what is the probability of Hannah choosing a single orange sweet..............?
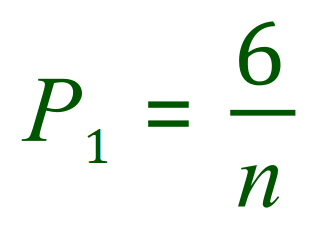
Where P1 is the probability of pulling out a first orange sweet, as there are 6 in the bag and "n" possible permutations. Pause for a moment if you want to, study this to make sure that you are happy with this has come from. Don't carry on until you are happy that you understand why it is 6/n.
OK.....let's carry on.....
We are told that Hannah eats the sweet, and then draws out a second sweet which is also orange, eating that one as well. What we need to do now is work out the probability of Hannah drawing out a second orange sweet. We know that there were six, now there are five and we know that there were initially "n" sweets in the bag, but after the first one was taken out this of course reduced to "n-1".
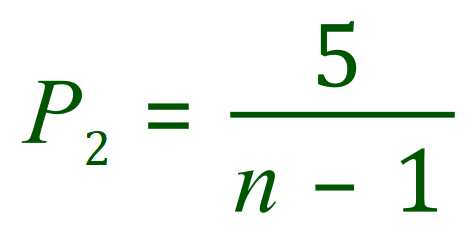
We are told that the probability of Hannah drawing out two orange sweets in succession (i.e. P1 then P2) is one third. Now we know from our knowledge of the multiplication rule of probabilities that the overall probability of these two events is the product of them both, in other words PE = P1 x P2

P1 x P2 = 1/3 as shown above, and also this is a piece of the information which is given in the question.
What we have to do now is tidy up the expression that we are left with, first of all multiply the left side fractions together:
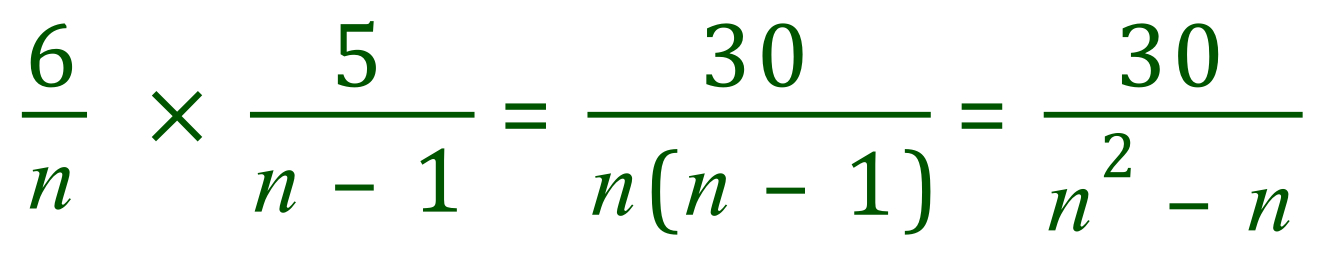
And also we know that this is equal to 1/3:
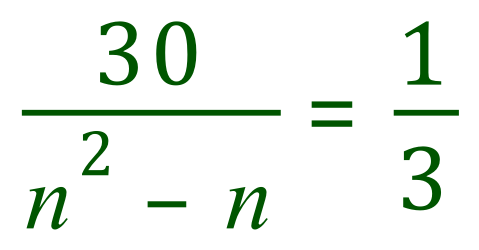
Now multiply throughout by 3 to remove the fractions:
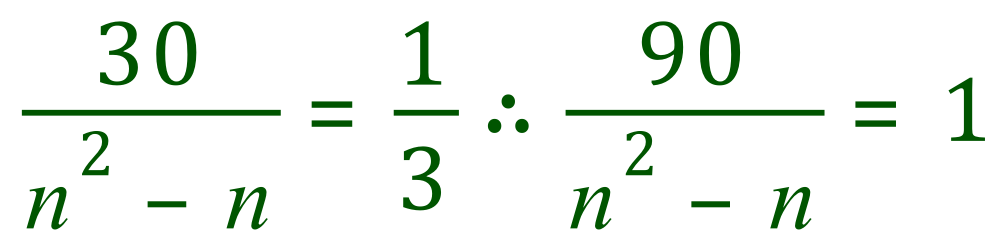
Now, stop at this point and think to yourself "if we have a fraction that is equal to 1, the numerator must be the same as the denominator?" If you can see this, carry on if not just pause for a moment until it becomes clear.
This leads to:
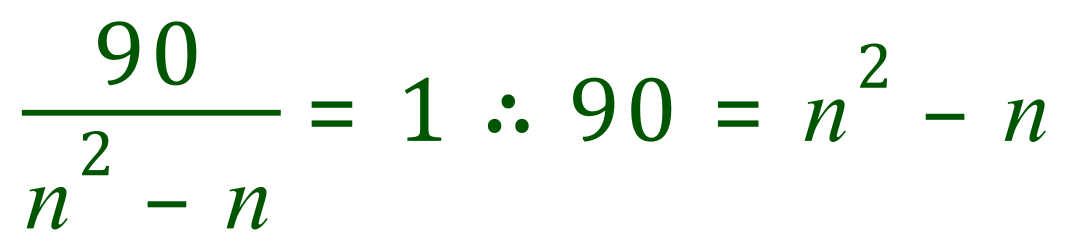
Rearranging:
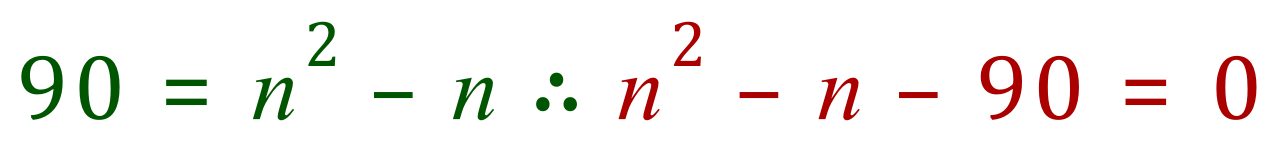
And the section highlighted here in red is the answer to the problem posed by Hannah's Sweets !
Back To >> Question <<