This rule deals with events which are dependent or independent and in this particular part of the section we will take a look at examples of both types.

Let us suppose that we have a bag containing 50 balls, 16 are red, 25 blue and the remainder (9) are white.

What is the probability of pulling out a red ball?

You should be able to see this:

Note that the result is always simplified if it can be.

Likewise the probability of pulling out a blue ball is ½ and the probability of pulling out a white ball is 9/50.  If we pull out a blue ball, put it back and then pull out a white ball the overall probability of this happening is this:

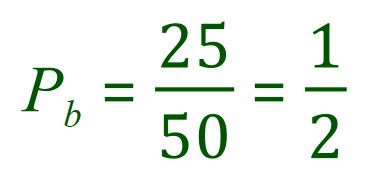
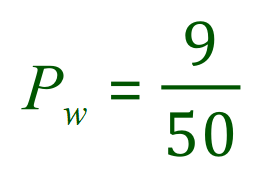
This result of course is heavily dependent on the fact that we put the blue one back first.  Because we do this the selection of the second ball is not influenced by the results of the first and these events are called “independent events”.

Let us assume that this time we pull out once again a blue ball (purely by chance of course) but this time we keep it out of the bag.  Again purely by coincidence we then pull out a white ball.  What is the overall probability of this chain of two events taking place this time?

Just like the last time:

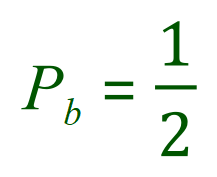
However the probability of the white ball being selected this time has been modified slightly, or affected by, or “is dependent on” the first result:

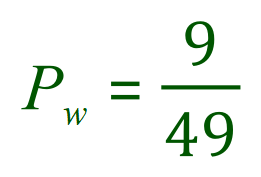
We still have 9 white balls, but overall we have lost one so the denominator of the probability fraction shown above must change to show this.

Therefore the overall probability of selecting blue and then white:

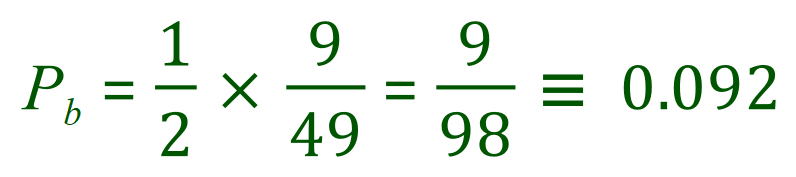
The events have become dependent because one of them influences the outcome of the other.  Care must be taken in probability questions when deciding whether or not events are “independent” or “dependent”.

As we have seen above, two events are independent if the probability of the first event happening has no impact on the probability of the second event happening. If the probability of one event happening affects the probability of other events happening, then the two events are not independent.

Example 2:

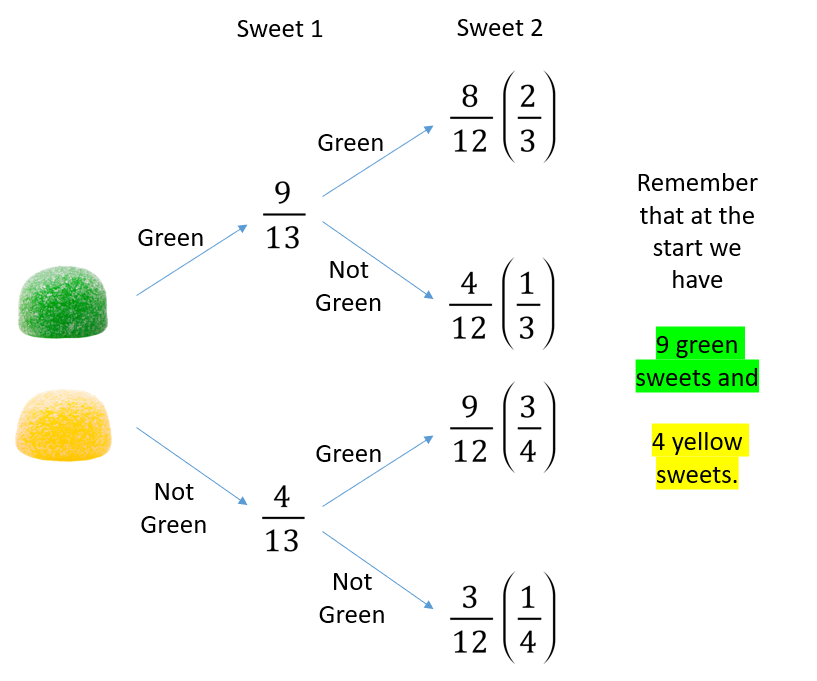
A bag contains coloured sweets. In the bag there are 5 yellow sweets and 9 green sweets. A sweet is removed:

(a) what is the probability that the sweet removed is green?

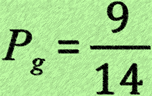
(b) now, the first sweet is put back in the bag and another taken, what is the probability that the sweet this time is yellow?

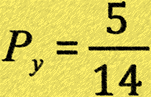
Now we ‘muddy the waters’ a little bit.

(c) a sweet is taken from the bag, it is a yellow sweet and is eaten. What is the probability that the next sweet removed is also yellow?

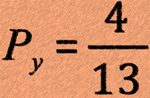
The probability has changed from 5/14 to 4/13 because a sweet being eaten has altered the probability for the next event.

What is the probability that the next two sweets 
(neither will be put back into the bag) 
withdrawn will be green?

Remember that we now only have 13 sweets in the bag.

So…………

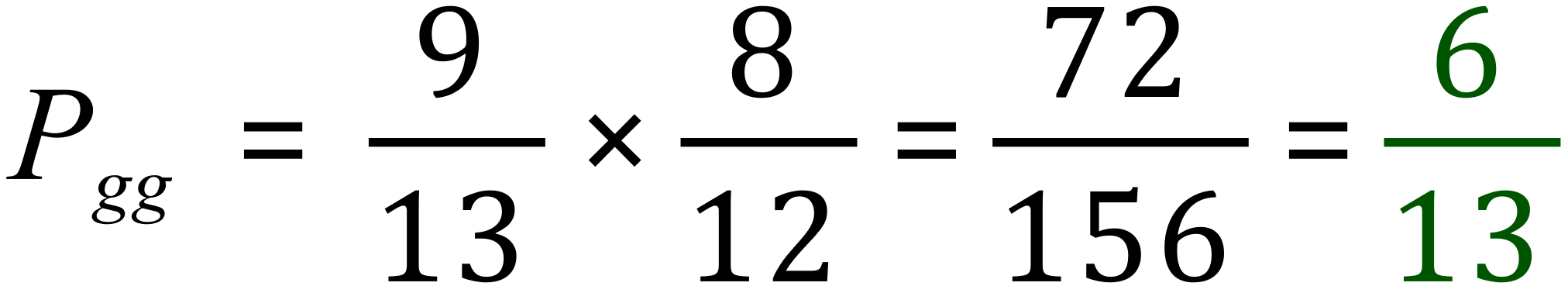
Back To >> Hannah's Sweets <<