Probability
There isn’t much in life that we can predict will happen with absolute certainty, or say, with similar certainty that it won’t happen. We can only estimate the “likelihood” of something happening, or not happening and sometimes this can be guided by previous outcomes, for example a football team performing rather badly or a horse in a horse race which hasn’t won any races for quite some time you might consider these to be unlikely to succeed, or to put it another way they will probably lose. The likelihood of something happening or not happening is defined this way, we say that the probability of an event is a measure, or estimation, of how likely it is to happen.

Most maths books dealing with the subject of probability start with the tossing of a “fair” coin. We say “fair” because if the coin was double sided the probabilities are biased (if it’s a 2 headed coin you just can’t flick a tail, it’s as simple as that).
We measure probability on a scale of 0 to 1, where 0 is an absolute impossibility and 1 is an absolute certainty. It is usual to indicate a probability value as a decimal number or a fraction. An absolute certain event has a probability value of 1 and an absolute impossibility has a probability value of 0.
Example: “what is the probability of a human being running a 1 minute mile” and of course the answer is 0 this is impossible (at the moment anyway), taking into account the fact that human beings can run at speeds around about 15 miles an hour in bursts.
Example: “what is the probability of an object falling to the ground on planet Earth if I let go of it” and of course the answer here is 1 because under the force of gravity all objects will fall to the ground if released (excluding helium balloons etc, try to humour me here 8-))
So, how do we measure probability, how do we actually define what it is?

The probability of an event occurring is the quotient of the number of possible ways that the event can occur divided by the number of possible outcomes in total. This probably sounds quite confusing so I will explain with a simple example using a tossed coin.
As you can no doubt appreciate, although not shown this coin has 2 faces, what we commonly refer to as the “head” and the “tail”. If we were to this coin into the air and let it fall to the ground it would land on one side or the other. The fact that the coin has to land on one side or the other gives us our one value “the total number of possible outcomes” if we flick the coin up in the air, hoping for it to land with the head side facing upwards we know that this can only happen one way because there is only one head side and this gives us our second value which is “the number of desired outcomes”.
If we put the 2 together we get this:
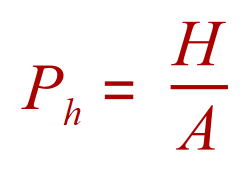
Where Ph is the probability of "tossing a head", H is the number of ways in which a head can be obtained and A is the total number of all possible outcomes (in this case heads and tails). So we can see that the probability of tossing a head result is one half (Because using a proper coin, there is only one head so a head can only be obtained in one way, but the alternative outcome is that there could be a head or tail so in this case there are 2 possible outcomes, the probability of tossing a head is therefore one out of two).
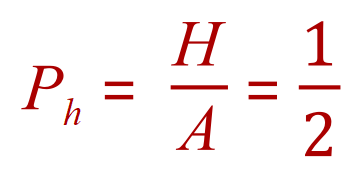
I’m sure you’ll understand that if the probability of tossing a “head” is a half then the probability of tossing a “tail” is also a half, another way to look at this is to say that the probability of tossing a “tail” is 1 minus the probability of tossing a “head” (The reason for this should be quite obvious. If you toss a coin, there has to be an outcome (which is a certainty =1). Half of the time you will receive a head so it stands to reason that the other half of the time you will receive a tail, so the probability of "tossing a tail" is 1 (a certainty because you have got to get something) minus the probability of "tossing a head").
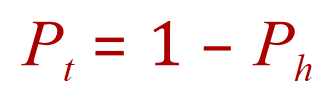
This will become more useful when we start looking at events with more than 2 total outcomes, and we are going to go there now:

Let us consider a “fair” die, and once again I state the word “fair” because some unscrupulous establishments whose businesses rely heavily on the use of dice have been known to “weight” dice to ensure that the result of throwing the dice is biased (and of course to their benefit). As we now a die is a 6 sided three-dimensional shape (a cube) with numbers ranging from 1 to 6 represented by dots. The opposing sides of a die always add up to 7. If we throw a “fair” die then the chances of scoring 1, 2, 3, 4, 5 or 6 are equal.
What is the probability therefore of throwing a single die and scoring 5? Consider the following equation:
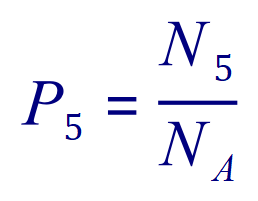
Where P5 is the probability of throwing a 5 with a single die, N5 is the number of ways in which 5 can be scored with a single die, and NA is the total possible number of outcomes with the single die.
Study the equation, think of this “how many ways can I roll a 5 with one die?”, Well of course you can only roll it once that way because there is only one 5 on a single die, but considered the next part of the question “how many possible results can I have from one single sided die?” And you should conclude quite quickly that there are 6 possible outcomes because a die has 6 faces, so the chances of you rolling 5 using a fair die (and any other of its results for that matter) is 1/6, or put as an expression:
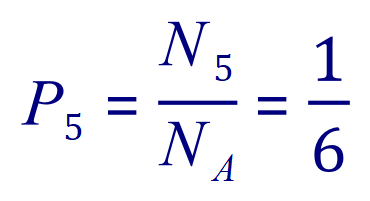
There are mathematical expressions in probability which define, or formalise some of the expressions I’ve used above:
- Sample Space = “the total number of outcomes”
- Sample Point = “one of the possible outcomes”
- Event = “the result which gives you your Sample Point”
- Experiment = “the action performed resulting in an event or set of events”
So just to make this clear, in the rolling of a single fair die the “experiment” is rolling the die, the “event” is when we receive our result, the “sample space” would be the numbers 1 to 6 inclusive and the “sample point” would be the outcome we received.
Let’s move on and take a look at a pack of cards.
In a standard pack of playing cards we have 4 suits with 13 cards in each; we have an ace, 2 to 10 inclusive and a Jack Queen and King. For the purposes of what we’re going to do we will ignore the jokers so we are playing with 52 cards.

Let’s ask ourselves a few questions about playing cards:
- Drawing out a card at random and completely blindly what is the probability of it being a red card? Well half the pack is red and the other half is black, so the likelihood of picking out a red card is 26/52 which if we simplify this becomes a half.
- Drawing out a card at random and completely blindly what is the probability of it being a picture card? Well as you can see from the picture above there are 12 picture cards in a normal pack so the probability of picking out a picture card is 12/52 which if we simplify becomes 3/13.
- Drawing out a card at random and completely blindly what is the probability of it being the 6 of clubs? In this particular case there is only one 6 of clubs in the pack so the probability is therefore 1 out of 52, or 1/52 as a fraction.
- Finally, drawing out a card at random and completely blindly what is the probability of it being the “Ace of Spades” or the “Queen of Clubs”? In this particular question we are being given the opportunity to look at 2 possible outcomes, we are increasing the probability by looking at what is called a Boolean condition, that is one result OR another result. The probability of the card being one of them or the other is therefore 1/26.
In probability when we look at an “OR” condition we add the probabilities together of the 2 separate events. For example for the card to be an “Ace of Spades” the probability has to be 1/52 because there is only one such card in the whole pack, similarly for the card to be a Queen of Clubs the probability again is 1/52 because again there is only one Queen of Clubs in the whole pack. Therefore we can write the expression this way:
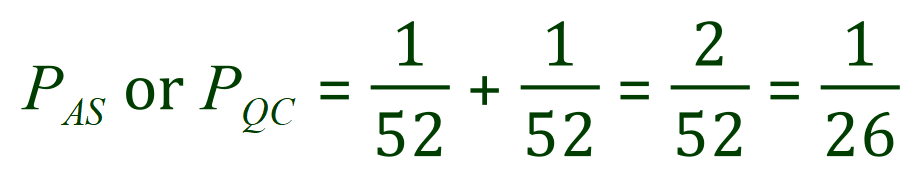
We can extend this by saying “what would be the probability of the card being any of the kings?”
Well, what is the probability of it being the “King of Spades”? As there is only one “King of Spades” in the whole pack the probability has to be 1/52. The same applies for the King of Hearts, King of Clubs, King of Diamonds because the probability of a single card being any one of those exclusively is 1/52 but when we consider the “OR” conditions the probabilities are added together:

If you think about it, it makes perfect sense because the probability of picking one card out of 52 is of course 1/52. When you make it conditional using OR you reduce the odds (you can see that the likelihood of picking any king must be greater than the likelihood of picking any particular king outright, you have 4 chances against 1). “OR” and “AND” conditions can become quite complicated, we will consider these further soon.
>> Questions <<