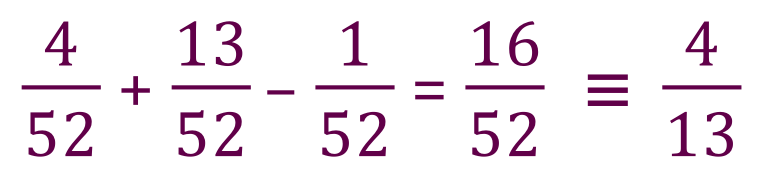Exclusivity - The Addition Rules
There is a general rule called the “Addition Rule” and this states that:
“When two events, let’s call these A and B, are mutually exclusive, the probability that A or B will occur
is the sum of the probabilities of each individual event”.
Okay, so what do we mean by “mutually exclusive?” - Well, if 2 events are mutually exclusive, the probability of one of them happening is not dependent on, or influenced by, the outcome of the other and vice versa. For example if we roll a die and get a 5, then we roll it again and get a 3, then the outcome of getting a 3 did not depend on getting a 5 the first time round.
There are many instances of this if you think about it, let’s take a bag of marbles for example concerning 12 blue, 7 red and 4 yellow (making 23 marbles in total in the bag). If we randomly choose any one marble from inside the bag, the probability of it being a blue is 12/23, the probability of it being red is 7/23 and the probability of it being yellow is 4/23. Whether or not you pull out a blue, red or yellow is not dependent on what you pulled out previously, and the results of this particular selection does not determine, or govern or influence what happens the next time - the probabilities are mutually exclusive.
Okay, so I can hear you say to yourself “well what does “non-mutually exclusive” mean? Well events that are non-mutually exclusive have some form of influence over each other, or the results of one can show some sort of dependency on the result of the other. Let’s take a look at an example, and this might make it a bit clearer:
Let’s go back to our pack of playing cards, what is the probability of pulling out a king or a Queen?
Well as there are 4 Kings in the pack, the probability of pulling out one of them is 1/13, likewise as we have 4 Queens in a pack then the probability of pulling out any one of them is also 1/13 so the probability of pulling out a King or Queen is 1/13+1/13 which is 2/13.
Now if we change the situation and say “what is a probability of selecting a diamond or a 2” then we have to look at it this way:
We have 13 diamonds in the pack so the probability of choosing a diamond is 13/52 or 1/4 and the probability of choosing a 2 is 4/52 or 1/13 (because we have 52 cards in the pack, 4 of which are 2’s, therefore our odds are 4/52 which reduces down to 1/13).
The probability of our choice therefore being a 2 or a diamond is ‘almost’ 1/4+1/13 but not quite, pause for a moment and see if you can understand why.
The events are not mutually exclusive because when we select our card and hope for a 2 or a diamond, we could in fact select the 2 of diamonds which gives us both options in one go. If we consider the probability of selecting a 2 independently from the probability of selecting a diamond, then our results of one out of four (diamonds) and 1/13 (twos) ends up including the 2 of diamonds twice so we have to take it away at least once. The actual probability then in the case of non-mutually exclusive events is this:
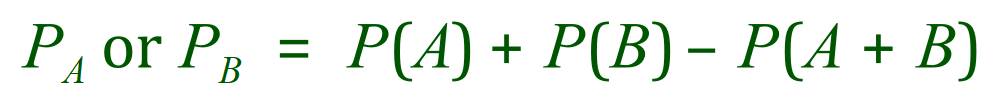
What this basically means is the probability of choosing a diamond or the probability of choosing a 2 is the sum of the probabilities of either event minus the probability of both events occurring simultaneously.
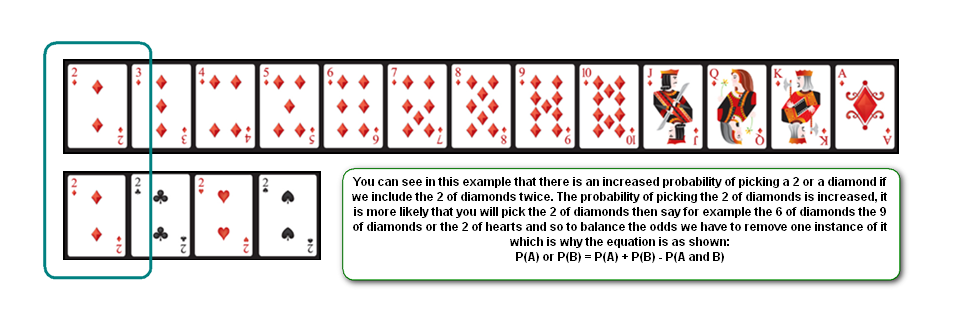
What we are effectively doing, is taking into account the overlap and this would normally be shown using the overlapping circles of a Venn diagram.

The two addition rules for probability are normally described like this:
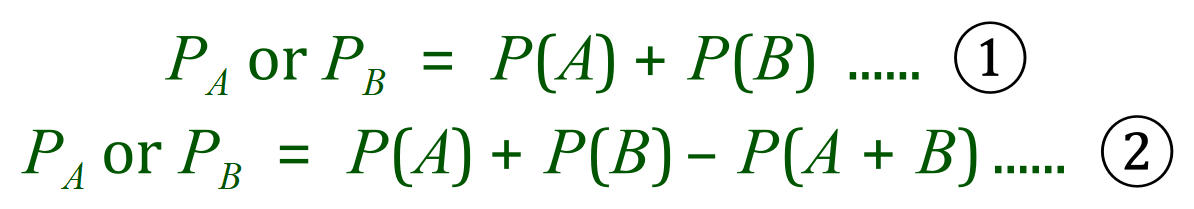
The first of the two rules is usually referred to as “Addition Rule 1” and the second is referred to as “Addition Rule 2” referring to mutually exclusive events and non-mutually exclusive events respectively but you can usually apply the second rule to events where the first rule would normally apply.
Back to Coins....
For example if you consider the tossing of a coin the probability of “tossing a head” is one half and the probability of “tossing a tail” is likewise one half, therefore the probability of tossing either one or the other must be one, in other words it’s a certainty that if you flick a standard coin you will get a head or tail, the probability of getting both with one flip of a coin is zero so you can see that the first or second rule can be applied here.
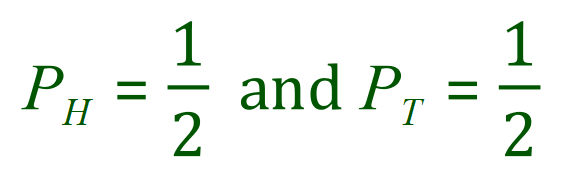
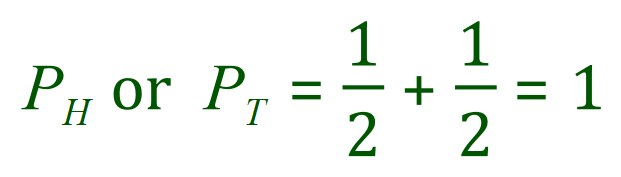

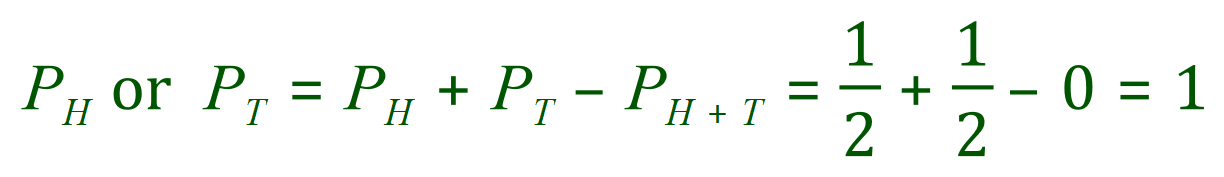
Example:
The probability of a businessman owning a Rolls-Royce is 0.6 and the probability of a businessman being a millionaire is 0.8. The probability of a businessman being a millionaire and owning a Rolls-Royce is 0.5.
If we pick one businessman at random, what is the probability that he will either be a millionaire or own a Rolls-Royce?
Solution:
Let the probability of owning a Rolls-Royce be P(R) and the probability of being a millionaire P(M), and that the probability of being both is P(R+M) = 0.5
P(R) = 0.6, P(M) = 0.8 and P(R+M) = 0.5
Using the appropriate rule for non-mutual exclusivity:
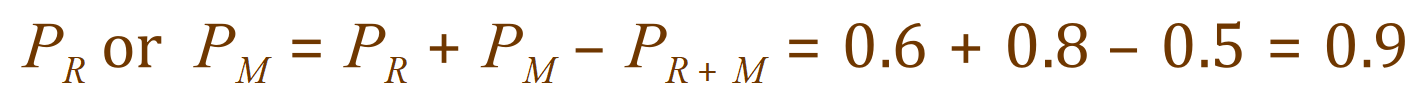
Therefore we can see that the odds are very high indeed of our businessman either being a millionaire, or owning a Rolls-Royce. In fact 0.9 which is 90%.
Summary: Mutually Exclusive Events Can’t Happen Together
Summary: Non Mutually Exclusive Events Have A Degree Of Overlap
Eg: Head or Tail from a single toss of one coin – these are mutually exclusive because you can’t get both results simultaneously, however you have to have one of them so the outcome is a certainty = 1.

Eg: Drawing a King OR a Spade from a deck of 52 playing cards is a non-mutually exclusive event because both can happen (King OR Spade OR King of Spades), this has the probability of:

So the probability of drawing one or the other is: