The Intersection and The Union
Although it is quite proper to use the “and” and the “or” expressions, probability has its own symbols for these, the symbol representing an “intersection” and the symbol representing a “union”.
When we consider the probability of 2 events, let’s call them A and B, we use these symbols as shown below:
“The probability of A or B”

“The probability of A and B”

Perhaps the easiest way to remember the distinction is to say that the symbol for “and” looks like a capital A with a rounded top but without the crossbar, and of course the “or” must be the other one!
A simple example using both of these symbols could be the tossing of a single “fair” coin:
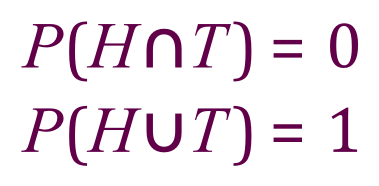
Study these two expressions for a short while and you will see that the first one is saying to you “If I flick a coin the probability of getting a head and tail must be 0, it’s impossible to get both results with one flick” and in the second example it is saying to you “If I flick a coin the probability of getting a head or tail is one, it is a certainty that I will get one or the other”.
Probability questions aren’t always set out in a straightforward way, there are sometimes some values that you will be given, and other times certain values you will not be given and you will be expected to work them out, take a look at the next example:
“In a class of 30 music students, 21 students play guitar, 14 students play the piano but some students play both. Work out the probabilities of a student playing guitar only, piano only or both”
(NB: as the question doesn’t actually specify, we take it that every student plays at least one instrument).
Quite nasty on the face of it, but let’s stop and take a look at it and we will do it in stages:
1. We know that 21 students play the guitar, but some of them might also play the piano.
2. We know that 14 students play the piano, but some of these might also be guitarists.
Indeed, the question actually tells us that some students play both, what the question doesn’t do is tell us how to account for that, so we have to do that ourselves. Let “n” be the number of students who play both instruments, so out of our 21 guitarists we could have a certain proportion of pianists. If we take away “n” from 21 will be left with the number of students who play only the guitar:
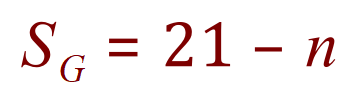
Similarly if we take away “n” from 14 we will be left with the number of students who only play the piano:
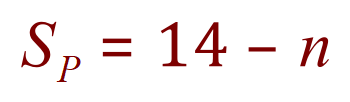
If we add up the number of students who only play the guitar, the number of students only play the piano and “n” which represents the number of students who play both, this must add up to 30:

Line 1 is a simple representation of the addition we need to make, line 2 is the same as line 1 but with the parentheses removed also in line 2 we can see that 2 of the n’s cancel out leaving us with the expression in line 3 of 35 minus n = 30 from which we can conclude that n= 5. We therefore now know that the number of students who play both the guitar and the piano is 5.
Now we can see that we have a mutually exclusive probability problem and if we were to represent this with a Venn diagram we would have 2 intersecting circles with the intersection showing the value of 5, one of the circle is showing the value 21 – 5 = 16 and the other showing the value 14 – 5 = 9.
From this we can state that the probability of a student at playing the guitar only is 16/30, the probability of a student playing the piano only is 9/30 and the probability of a student playing both is 5/30. We know that each student plays at least one instrument so the probability of the student playing the guitar or the piano must equal 1.
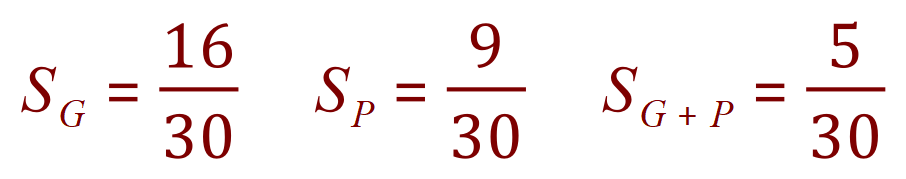
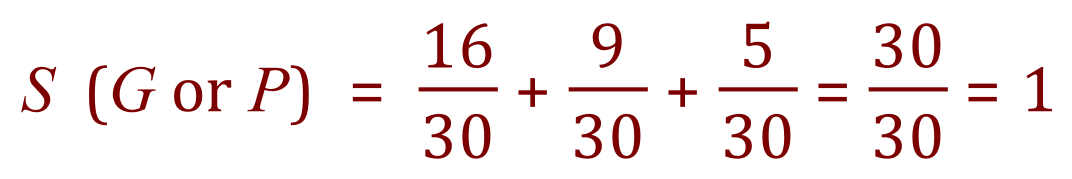
Using the well-known formula for mutually exclusive probability we can represent these values in a slightly different way, but still show that it works: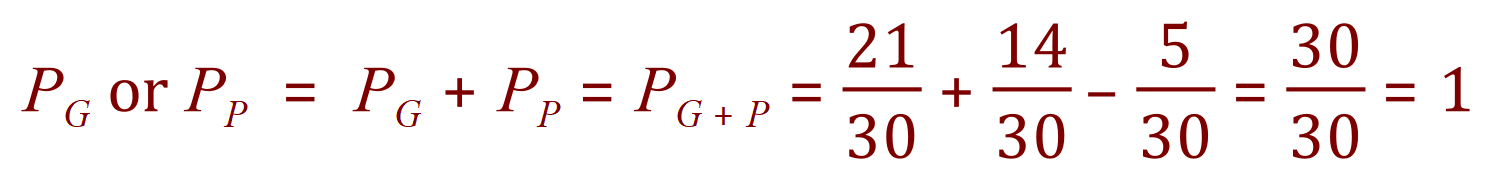
Now then, on this subject of using “n” we arrive at a convenient point to throw in the question that caused a lot of consternation in a 2015 UK GCSE mathematics paper.
The question appears quite disjointed but in fact it isn’t. I think that the reason most students struggled with the question is that they weren’t able to make the connection between the narrative part of the question and the proof required.
Let’s take a look at the question and see where we go.
Q1. Hannah has a bag of sweets containing "n" sweets. There are 6 orange sweets in the bag, the rest are yellow. Hannah reaches into the bag and pulls out one orange sweet and eats it, she then reaches back into the bag, pulls out a second orange sweet and eats that one too.
The probability of Hannah pulling out these 2 orange sweets in succession is 1/3. Given this information show that:
![]()
S1. Usually in probabilities we have a fixed number to choose from, for example "12 balls in a bag, 3 green and the rest are red", in other words a fixed number. In this case we are told that we have an unknown number given the variable "n". We are told that there are 6 orange sweets so the probability of choosing one orange sweet from a selection of "n" is:
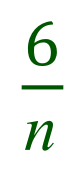
We are then told that Hannah reaches into the bag and takes out another orange sweet, because we know that there were 6 to start with we now know that there are only 5 to choose from, but how many sweets are now in the bag? Well we started off with "n" and we removed and ate one sweet. This would leave us with "n -1" total number of sweets in the bag, and the probability of choosing another orange sweet would therefore be:
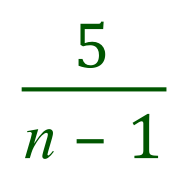
The probability of both events occurring is the product of the probability of each event, therefore we end up with:
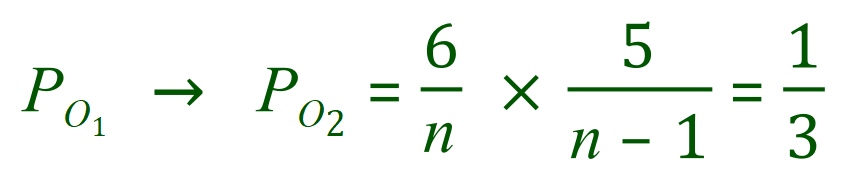
I'm using the arrow to indicate consecutive events in other words, PO1 and then PO2 have been shown as PO1 -> PO2 in the above equation. We are also told that the probability of this sequence of 2 events occurring, overall is 1/3. We now have a strange looking expression which eventually has to look like a quadratic equation in terms of "n".
Step 1: multiply out the fractions:
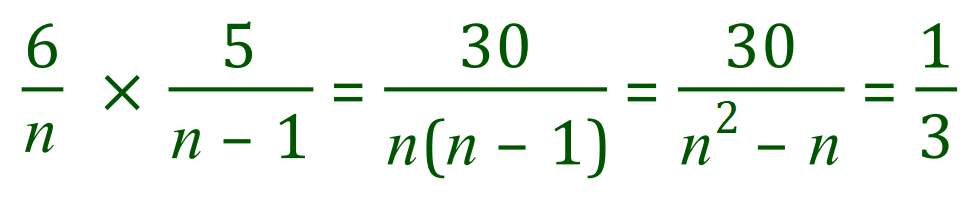
Step 2: multiply both sides by 3 to remove the fractional component on the right-hand side:
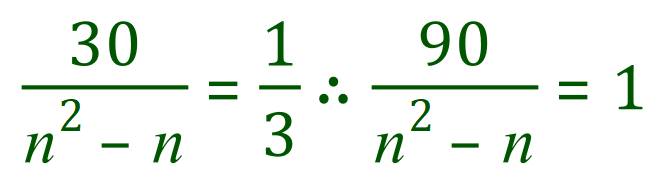
Step 3: Since the right-hand side of the overall expression (the right-hand side of the therefore symbol) equals one we can rearrange this to say that 90 =n2-n
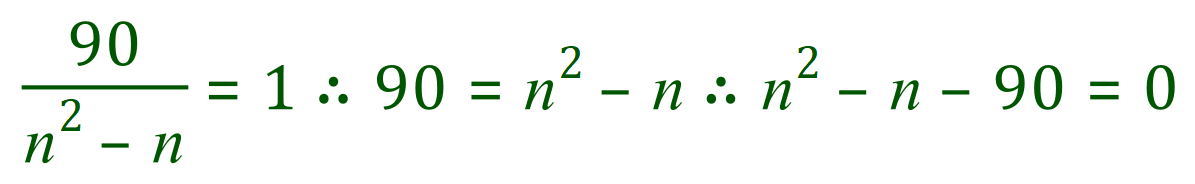
And at this point you have reached the end of the question.
Selecting two orange sweets in this way (that is the way the question said it was done) is an example of dependent events because the probability for the second selection is changed by the first one.