The Crocodile And The Zebra
A crocodile is stalking his prey located 20m further up a river, and on the other side. Crocodiles travel at different speeds on land and in water. The time taken for the crocodile to reach its prey can be minimised if it swims to a particular point “P” which is located “x” metres up river towards the prey, as shown.
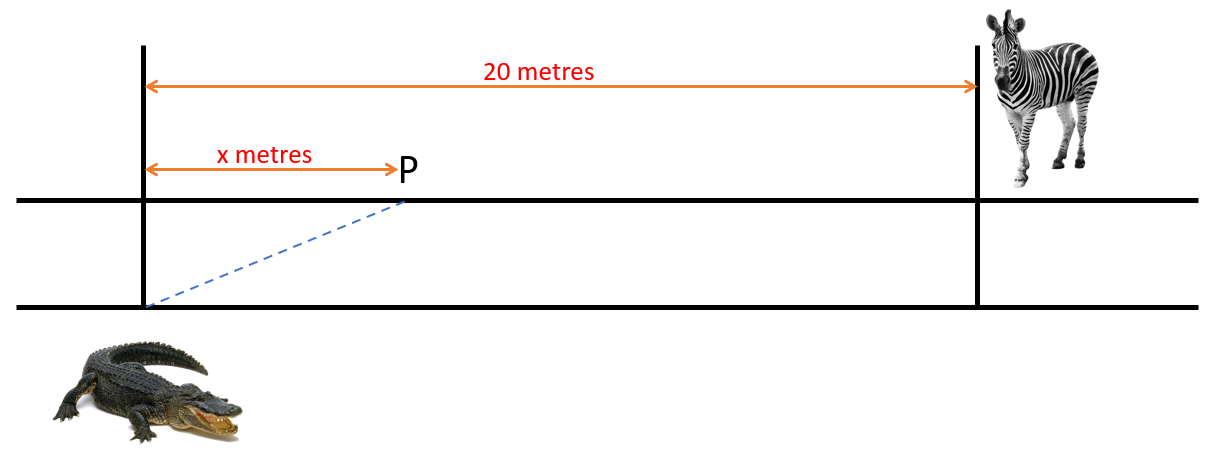
The time taken “T” measured in tenths of a second is given by:
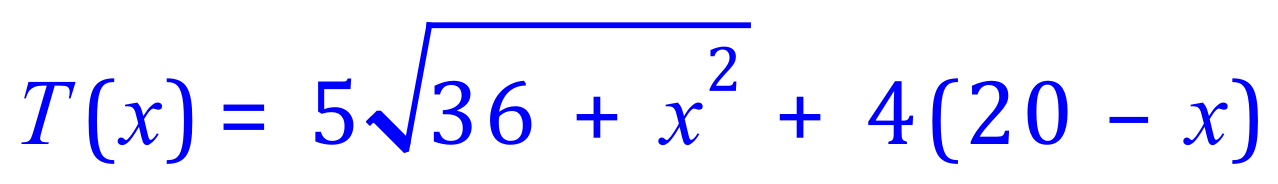
(a) Calculate the time taken if the crocodile does not travel on land.
(b) Calculate the time taken if the crocodile swims the shortest distance possible.
(c) Between these two extremes there is a value of “x” which minimises the time taken, find this value of “x” and hence the minimum possible time .
This question appeared on a Scottish Higher mathematics paper in 2015 and was the subject of controversy. Quite a ‘tasking’ question for the 16 year age group. Part (a) is quite straightforward, consider that if the crocodile does not travel on land, he must swim directly across to the zebra in a diagonal line, i.e.: the value of ‘x’ above is 20.
Substituting x = 20 into the equation given:
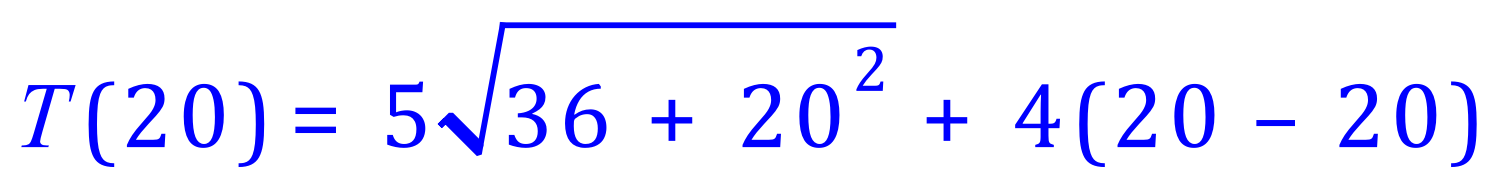

In the first equation, 4×20-20 of course equates to 0, leaving us with five times the square root of 436 which is 104.4, but don't forget these are in tenths of a second so we need to divide by 10 to come up with a of 10.44 seconds. This is the speed at which the crocodile can swim directly to his prey, without going onto land at all and is the answer to part (a).
In part (b) the crocodile swims the shortest distance possible, which, if you look at the diagram is directly across the bank so he is still 20 m away from his prey. This time the value for "x" is zero, and if we substitute this into the equation we arrive at another value for the time T.

Not much of a difference between 10.44s and 11.0s but I suppose that a hungry crocodile might want to try to reduce his time taken!!
Now….
This is where the tricky bit starts. The question does in fact SAY that there IS an optimum value for x where the time taken is minimised, i.e.: a certain value for x where the time is potentially lower than 10.44s and 11.0s (but it could be the lower of the two, we don’t know yet)….but how to establish this requires the use of Differential Calculus, and I’d guess that this is where the consternation arose.
The minimum value for T will occur when the first derivative of the equation equals zero, so the first thing we have to do is differentiate the equation. This requires you to remember your differential calculus and in particular the "sum" and "constant multiple" rules:
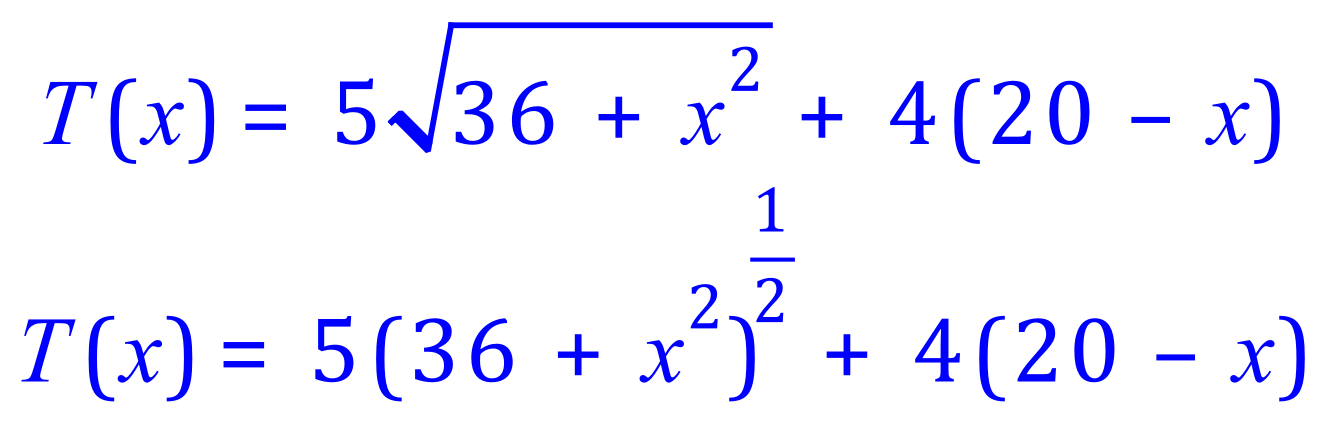
We have to apply differentiation to "a function of a function" multiplied by a constant, and then add to this the derivative of a smaller simpler second function. I will now "colour-code" the sections so that you can see what I'm going to do.

First of all, let's differentiate the purple bit, with respect to "x"
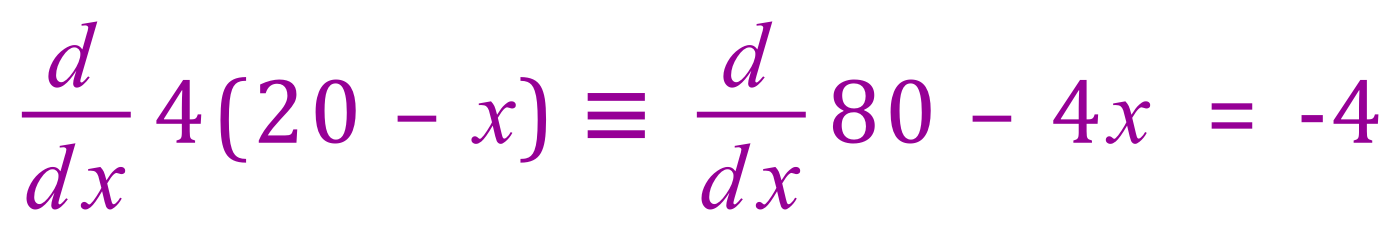
We will put the "-4" aside for later.
Now we need to look at the more complicated green bit, we have a function of a function and we need to apply the chain rule.
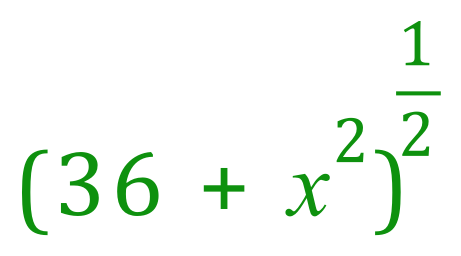
![]()

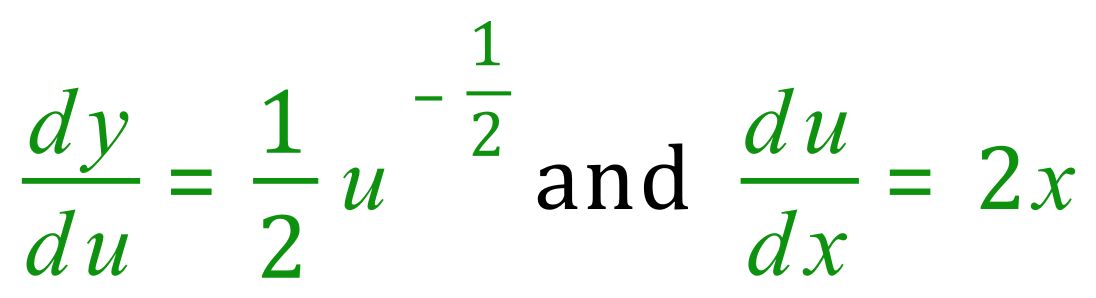
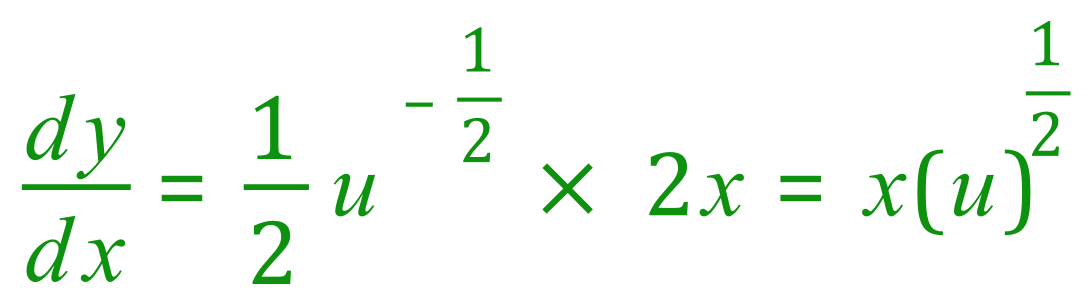
Now we substitute back for "u" and rearrange:
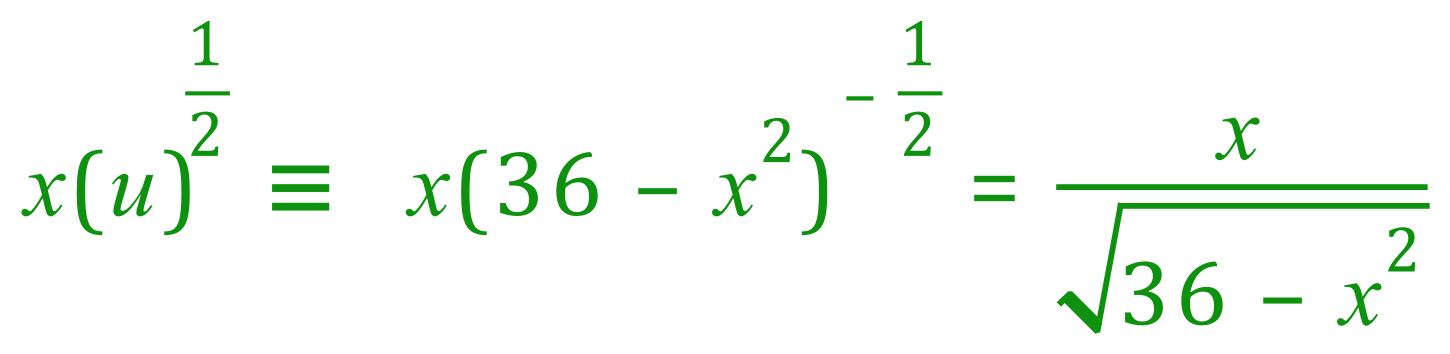
Cast your mind back to the beginning of this nightmare, we differentiated the last part of the expression and arrived at a value of "-4", also we started off with a constant multiple of "5" and we now need to recombine all of the sections to come to an expression for the change in T with respect to x:

We are almost there, we have said that the shortest, or most optimum value for x would be when the change in time with respect to x was zero, but in this mathematically we have to evaluate the above expression for a value for x when the whole expression equals zero.
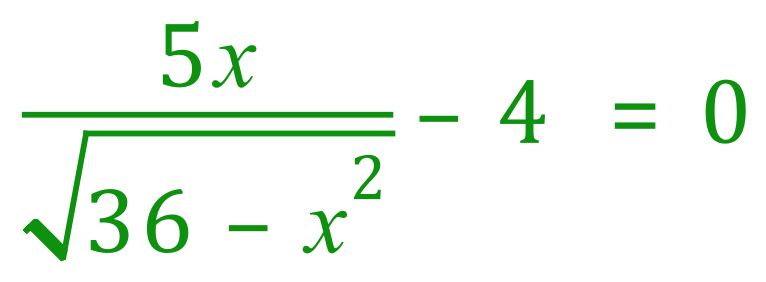
Step 1 : Rearrange:
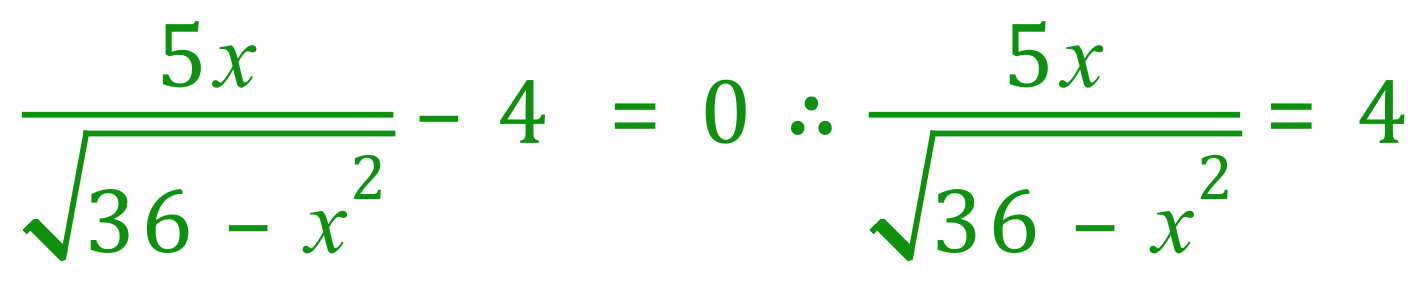
Step 2 : Square BOTH sides:
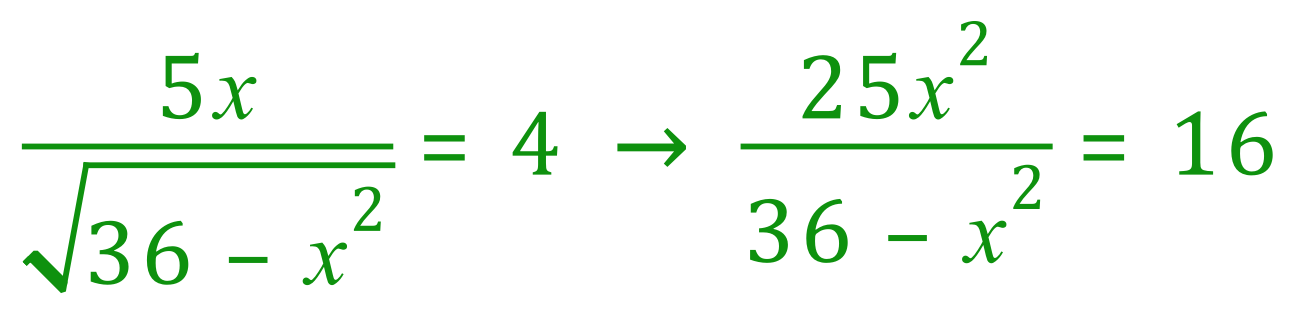
Step 3 : Multiply both sides by (36-x2)

Step 4 : Tidying up:
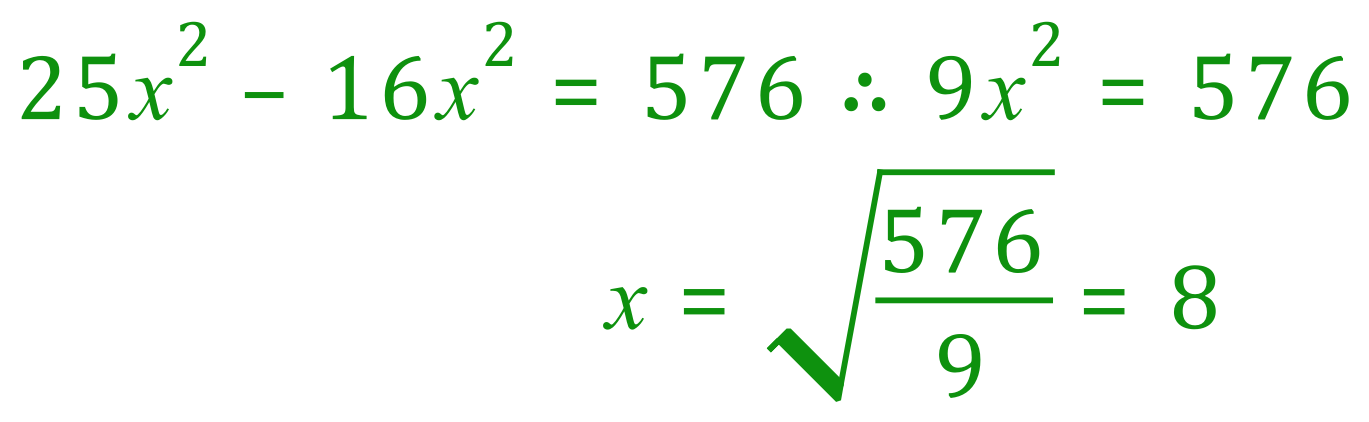
We have now established our optimum distance along the riverbank, this is 8 m. We know now then that if the crocodile swims diagonally across the riverbank to an 8 m point, then continues his journey on land, he will achieve an optimum time. We obtain this optimum time by entering x=8 into our very first equation at the start of the question:

The crocodile can get to the zebra almost a full second faster if he swims to a point P = 8m and then makes the rest of the journey on land.
Back To >> Question <<