Maximum Volume of a Box 1
Not really sure what else to call this question, and equally as unsure where I got it from, but it is a typical differentiation question so I thought it would be worthwhile to go through it.
An engineer is given a piece of sheet metal and is asked to construct a tank with a depth of "x" centimetres such that the volume of the tank is at its maximum. In other words, there is an optimum depth, or value for "x" which will maximise the volume of the tank. The dimensions of the sheet of metal are as given.
Find the optimum value for the depth of the tank.
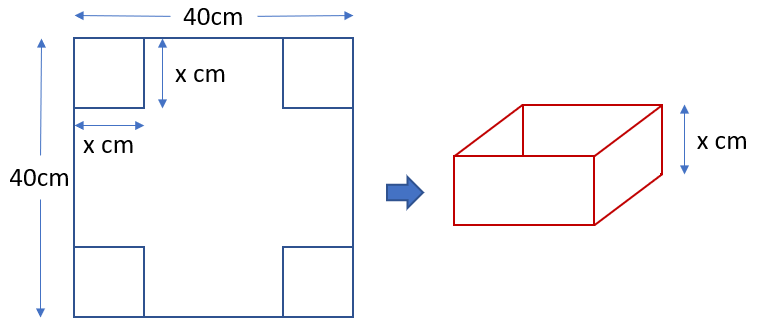
The first thing that we need to do, given the information we have, is to establish the values of all of the dimensions of the tank. We have a square of metal, 40 cm x 40 cm, from which we need to cut out four squares from the corners, of side "x" centimetres. If we do this first of all along the top edge, you should be able to see that the dimensions of the side of the square will be 40 - 2x cm.
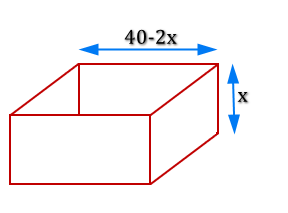
Make sure you can see where "40 - 2x" comes from, before you continue.
Given these values, we now work out, in terms of "x", the value for the volume of the box, and from our knowledge of cubes and cuboids you should be able to see where the following comes from, if not please stop and study it until you are happy to continue:

You should be able to see where this expression comes from, if not I can open it up and this should make it simpler, you are in fact simply multiplying the values of three sides:

If you are happy with what I've written above, feel free to carry on.
We now need to multiply this out to arrive at an algebraic expression for V:
Step 1: multiply the brackets out:
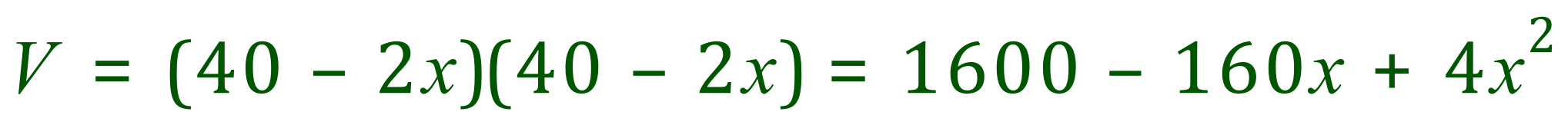
Step 2: multiply by "x"
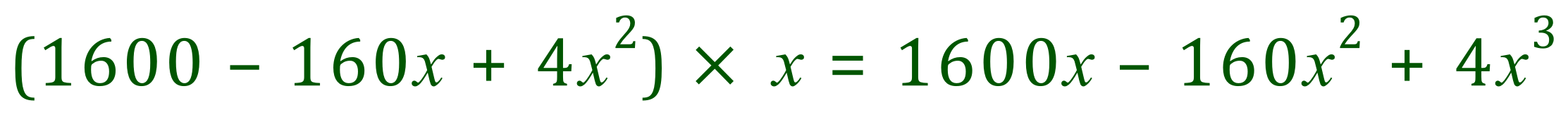
Step 3: Rearrange to a more familiar format:
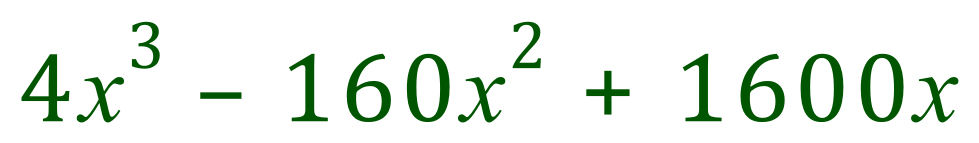
We now have to differentiate the above expression to try to establish a value for "x" which will give us a maximum volume:
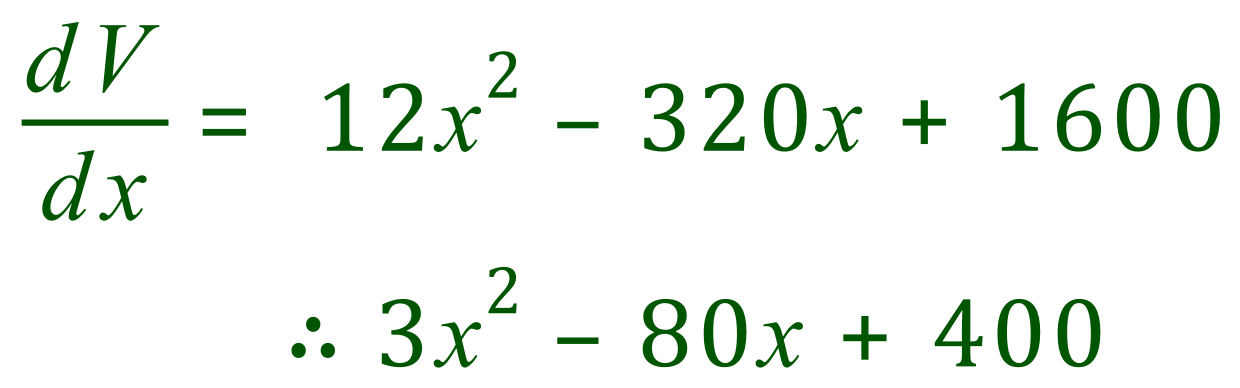
In the second line, all I've done is reduce the complexity by dividing by common factors. The expression that we are left with is an expression for how volume varies according to "x" and to establish the maximum possible volume we need to find a value for "x" when this expression equals zero, i.e. when there is no change in volume with respect to any variation in "x"
In other words we need to establish "x" when:
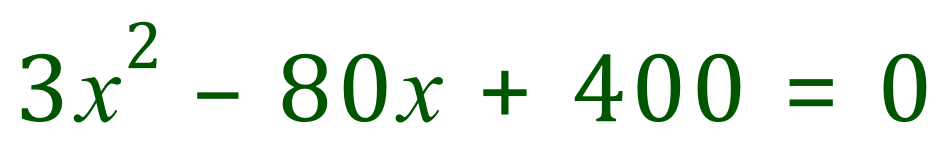
This is no more complicated than establishing the roots of the quadratic equation we are now left with, we cannot reduce the coefficient of X squared so we need to apply the rules to establish two numbers which, when added together come to -80 and which when multiplied together come to 1200. If you can't remember why this is the case, go back to the relevant section "Quadratic Factorisation - When The Coefficient of X Squared > 1" and refresh your memory.
Although it's not the most exciting way, and we could apply the quadratic function, I am choosing to list the factors of 1200 to see if I can spot a suitable pair of numbers, in fact as you will see it doesn't take long.
(1, 1200) (2, 600) (3, 400) (4, 300) (6, 200) (8, 150) (10, 120) (12,100) (15, 80) (16, 75) (20, 60)
Two numbers which add together give us -80 are -20 and -60, and when they are multiplied together they give us +1200 which is exactly what we want. Now we can rewrite our above quadratic in the following way:

If we group expressions and factorise them:
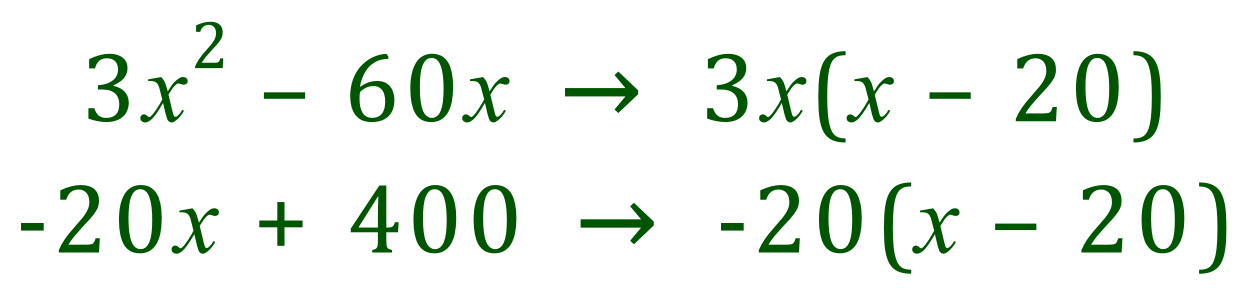
Our factorised expression therefore becomes:
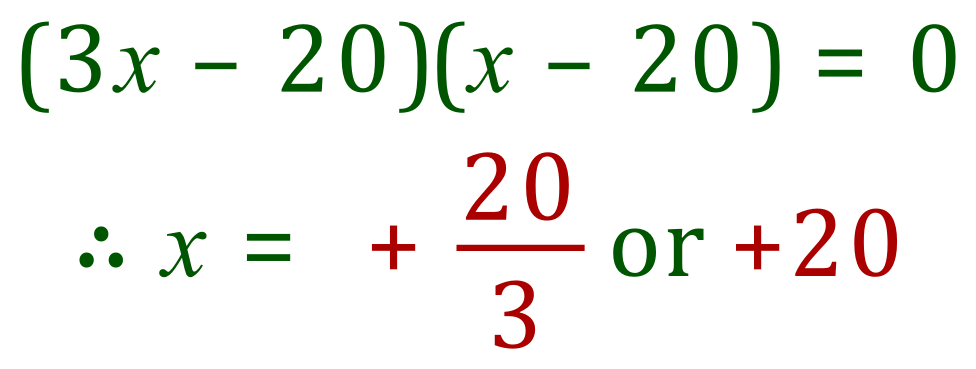
This means that one of the values for "x" is the optimum value that we've been looking for. You will quickly be able to dismiss +20 as 40 - 2x = 0 when the x equals 20, in other words we would have a box with zero volume!
Our optimum value for "x" is therefore:
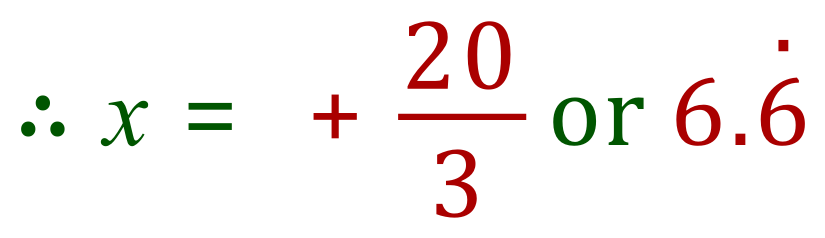
So we've established optimum value as 6.6 recurring, but can we prove this? Well, you wouldn't normally be asked to do this but just for the sake of satisfying myself that this is in fact the correct value I have entered values around 6.6 into the formula for the volume of the box with respect to "x" which appears at the start of the question.
The blue figures represent "x" at one decimal place and you can see that the value reaches a peak for the volume at 6.7 (which is what 6.6 recurring would be rounded to) after which there is a decline in volume. The red values take this to 5 decimal places where the decline is a little bit more prominent.

Back To >> Question <<