Maximum Volume of a Box 2
This question is a slight variation on the previous one. You are given the problem of producing a box/tank with the largest volume possible from a given amount of material.
Q. You are given 1200 cm² of sheet steel, you are to construct a tank with side length "x" and the depth "y"
(a) Calculate the optimum values of "x" and "y" so that the tank can hold the maximum possible volume of liquid.
(b) Calculate the maximum volume.
To start off with, it is always helpful to draw out a visual representation of what you're trying to achieve. Not unlike the box in the previous question we have here at least a basic visual idea of what the question is asking us for.
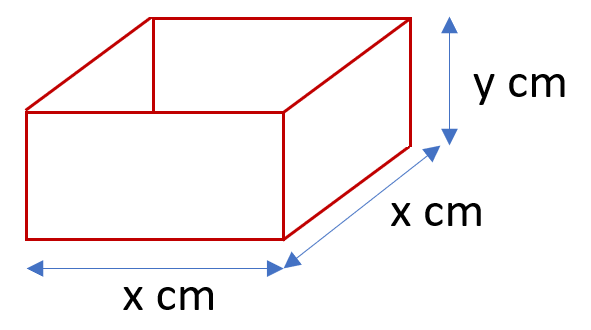
We need to make one square base, and four rectangular sides, the total area of which cannot exceed 1200 cm². We can represent this in terms of "x" and "y" thus:
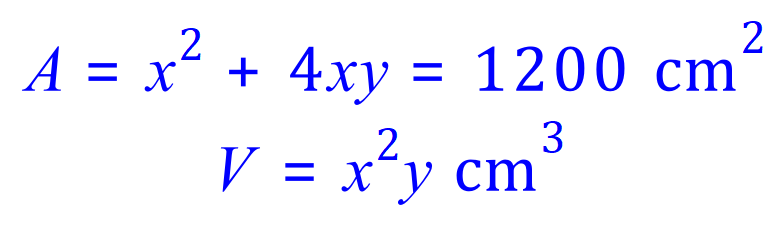
Stop at this point, and study the expression for A if you aren't sure where it came from. Do not proceed until you are happy. V remains unknown until the second part of the question, but we are able to express it algebraically as shown. When you are ready to, proceed.
We know that the maximum volume that this box can hold will give us values for "x" and "y" such that any change does not alter the volume of the box. What we need to do now is to find out an expression for "y" in terms of "x" as we need to produce an expression solely in terms of "x" which we can subsequently differentiate.
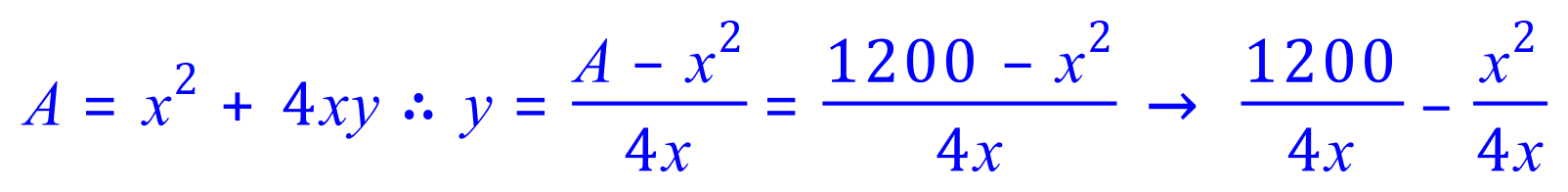
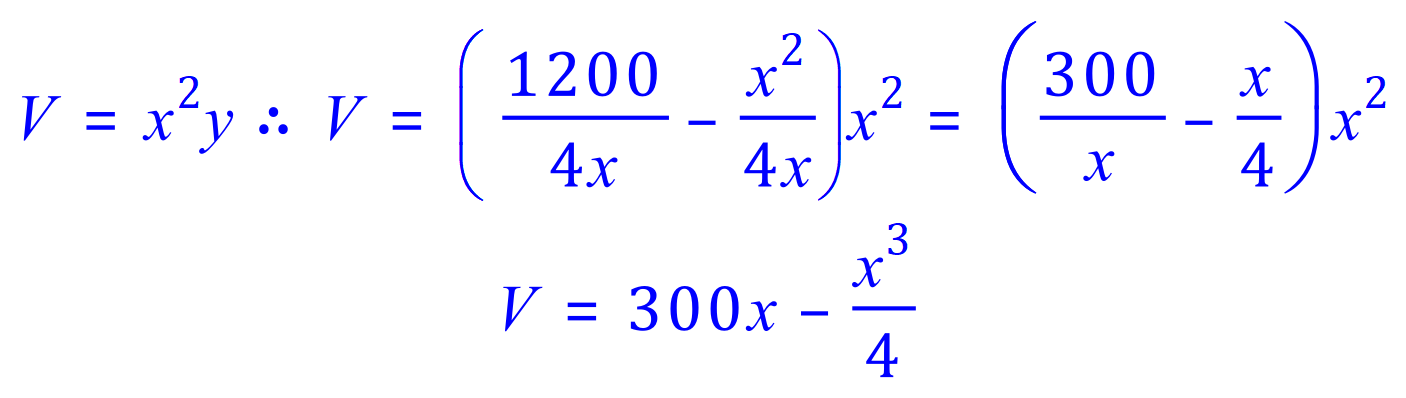
Once again, the algebra has become a little bit fiddly, make sure that you understand where the final expression V has come from, because the next step is going to be to differentiate it:
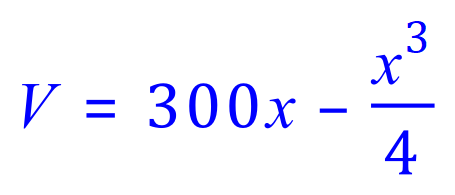
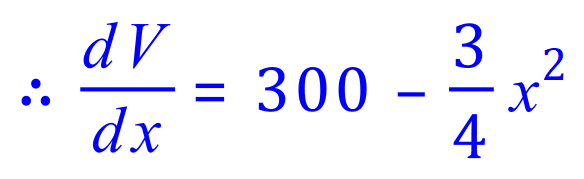
We need to now set this equation to 0, because it is only when this expression equates to 0 that the change in volume with respect to "x" doesn't alter, in other words we find out the value for x that we need:
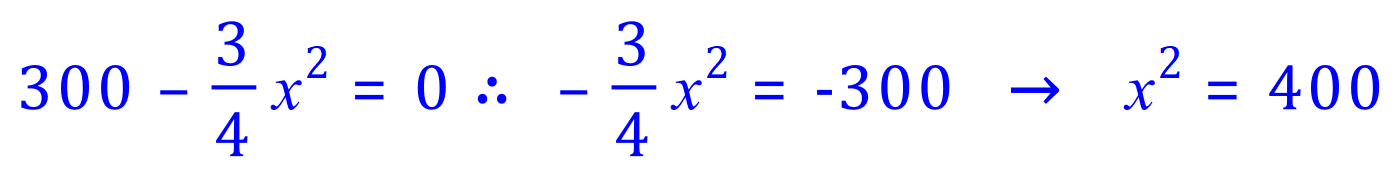
From this expression we find the requisite value for "x" is 20, and if we substitute this back into the expression for A, we can deduce a corresponding value for "y":
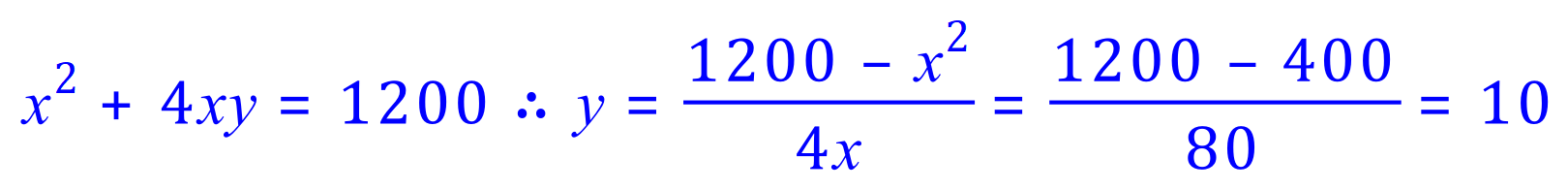

Now that we have values for "x" equals 20 and "y" equals 10, we can establish the volume of the box V:
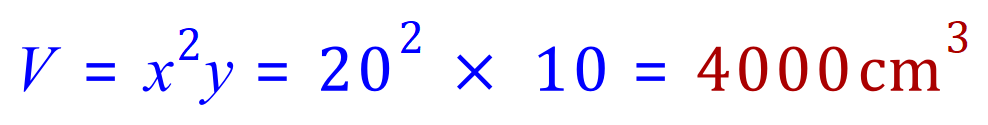
If you want to "back check" to make sure that you can do this out of 1200 cm² of material, look back at the expression for A:
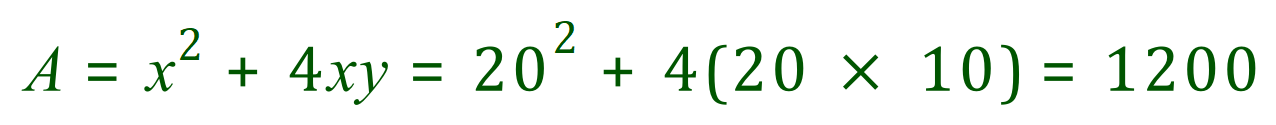
Back To >> Question <<