Overlapping Circles
A question which caused quite a stir in the EdExcel 2022 Maths Paper 1 in May 2022. Three overlapping circles and a requirement to evaluate the total size of a shaded area.
Here is the question:
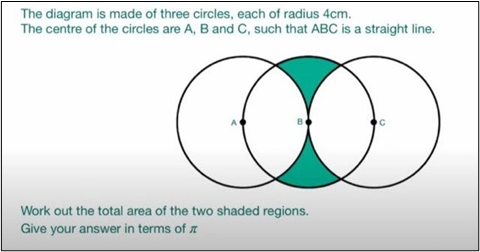
A challenging question but perhaps a little too demanding for 'timed examination conditions' especially as it was only a 5 mark question.
Here is how to solve it:
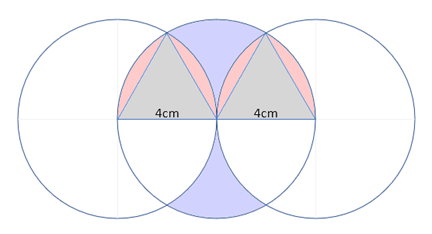
Of course you may not always have time to redraw the diagram, but a roughed-out version would suffice.
Above I have replicated the question diagram and marked out areas in different colours. The lilac coloured section is what we want to know the area of, but we also need the areas of the grey triangles and pink segments so that these can be subtracted from the SEMICIRCLE that houses them all.
The centre circle (upper half) holds 2 grey triangles and 4 pink segments, subtracting these from the area of the SEMICIRCLE that thet appear in will leave you with the area of one of the lilac sections. Doubling this result gives the final answer.
Let's see how this is done.
Step 1 - The area of each circle is calculated in the usual way:
Given the radius = 4cm, each circle has an area of:
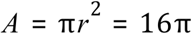
The SEMICIRCLE therefore has an area of half of this, or 8 pi.

Step 2 - Each triangle is equilateral and thefore has internal angles of 60o with sides of 4 cm (the given radii of the circles). Using the following information we calculate the area of the grey triangle:
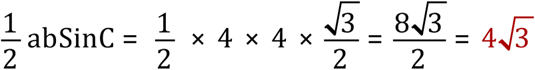
Step 3 - The SECTOR of the circle formed by the addition of a pink segment to a grey triangle has an area of one sixth that of the full circle, as it is 60/360 of the full circle, so:
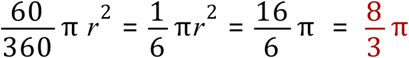
Step 4 - The area of the pink segment is therefore the area of the sector, MINUS the area of the triangle, or:
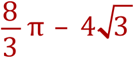
Step 5 - We now have enough information to start working the problem:
The top lilac area is therefore: 1 Semicircle – (4 Pink Areas + 2 Triangles)
Or, algebraically:
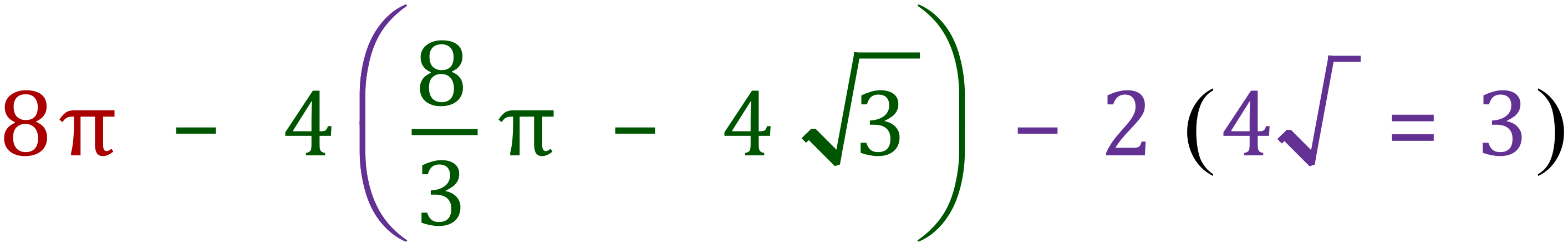
or
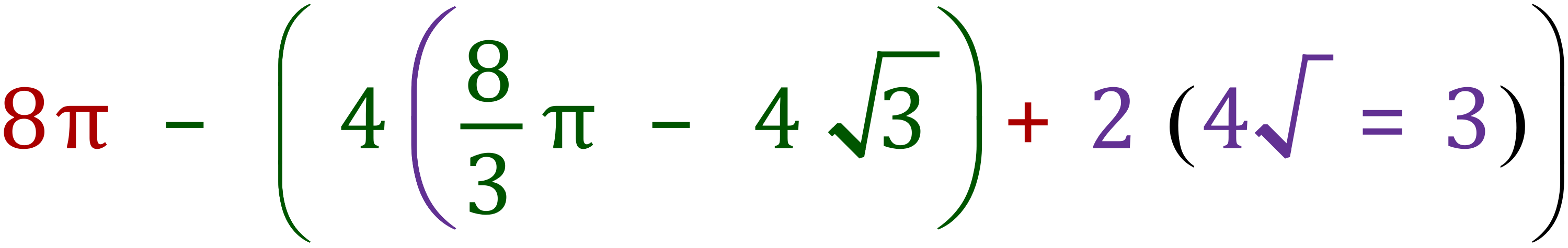
Step 6 - A bit of housekeeping (expand parentheses):
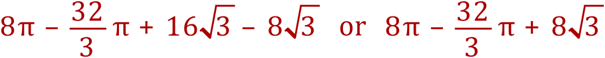
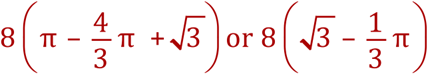
This is the area of the top lilac section. As they are identical, the answer to the whole problem is to double this final result:
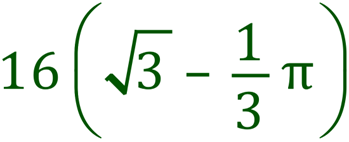
>> Back To Question <<