Addition and Subtraction of Negative Numbers
At the very beginning of the section on subtraction I did say “you can’t take 5 away from 4” and at the very beginning of your primary school education it would be left at that, however, I want to go through negative numbers very briefly to show you that you can in fact do this but you would be left with a negative answer.
We understand that:
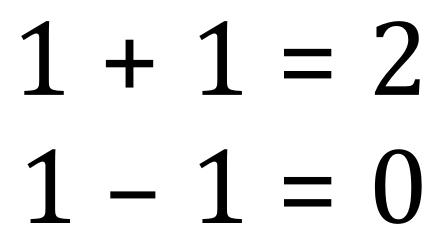
But what would happen if we took (in the case of the second equation) 2 away from 1?

Well to answer this will take a look at the number line which we will see more of later.
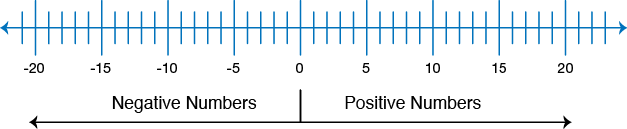
The number line starts at 0 which is called the origin and moves infinitely to the right along the positive scale and infinitely to the left along the negative scale. The first increment to the right of the origin is the positive number 1 and the first increment to the left of the origin is the negative number 1. Between each increment in the line shown above there is an infinite number of further increments representing the decimals/fractions so for example halfway between 0 and positive 1 we would have positive 0.5 (positive one half ) and halfway between the origin and -1 would have -0.5 (negative one half).
So, how do we add negative numbers? Well, before we answer that let’s just quickly recap on adding positive numbers by using the number line above:
Consider the very simple addition:

We know that this is correct, but let’s show it on the number line:
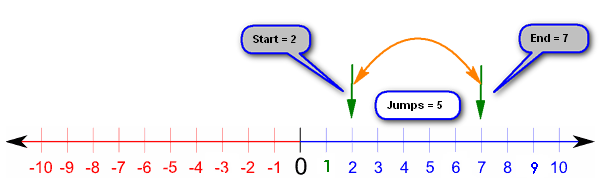
What we’ve actually done here is start at 2, then we have moved to the right 5 times in increments of 1 to arrive at our answer of 7, so what we’ve actually done as this:
2 to 3, 3 to 4, 4 to 5, 5 to 6 and 6 to 7
And if you count them, you’ll see that we have made 5 “jumps”
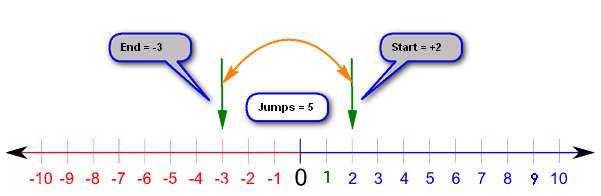
Now let’s take a look at this:
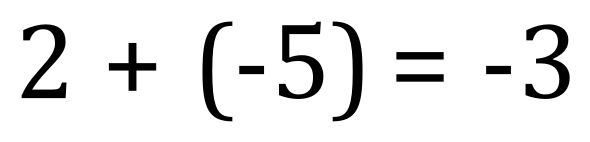
The answer is correct, at -3 because if you think about it, it can’t be 7 because that was the result of our previous example when we added +5, this time we are adding -5. Have a think about it for a minute, if “adding a positive number” means that we move to the right then it makes sense that “adding a negative number” means that we have to move to the left, but of course (in this case) with the same number of “jumps”:
Addition:
Adding a + moves us to the right
Adding a – moves us to the left
When we consider subtracting negative numbers, the method is slightly different.
You can see that above I’ve written two general rules for addition , the rules for subtraction slightly different to this and what I am going to do now, by taking a slightly different approach, is state the rules and use the next page or so to prove them.
Subtraction:
Subtracting a + moves us to the left
Subtracting a – moves us to the right
Well, this looks confusing? Yep…..bear with it!
Consider the expression:
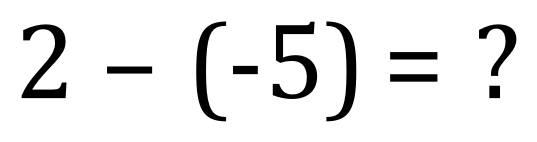
Well, what on earth could the answer be to this one? Once again, let’s go back to the number line:
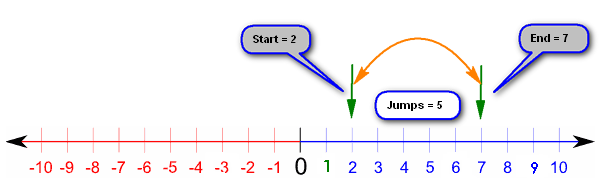
Now I know what you’re thinking, “this is just the same diagram that we used above when we worked out 2+5”… And you would be correct! Look at the second rule of subtraction above, where I stated that “subtracting a negative moves us to the right” so if we start with 2 and we are taking away -5 then strange as this might appear, we jump 5 places to the right not the left, therefore our answer is indeed 7. Let us show it is an equation:
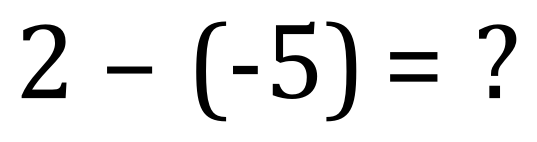
What this is telling us is that if we subtract a negative number we effectively add what would be the positive version of that number to the first number:
Study these examples and hopefully this will become clear:
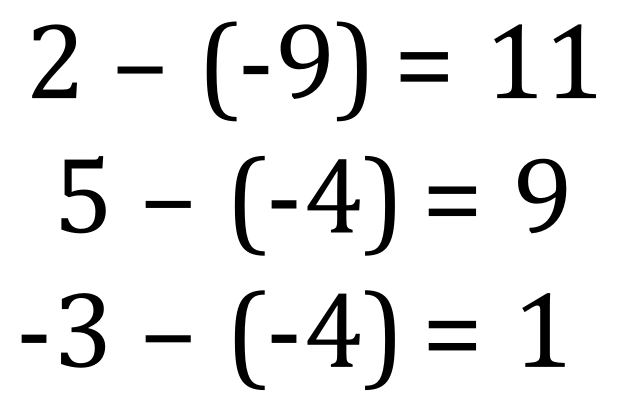
Now….let’s take a look at the first rule of subtraction now which states that “subtracting a positive moves us to the left”
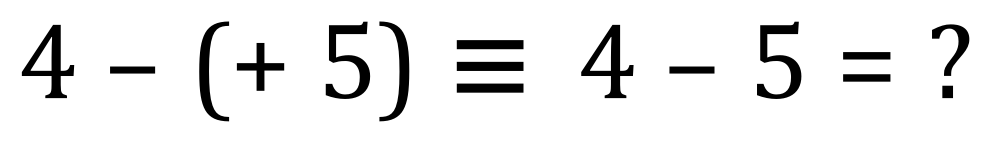
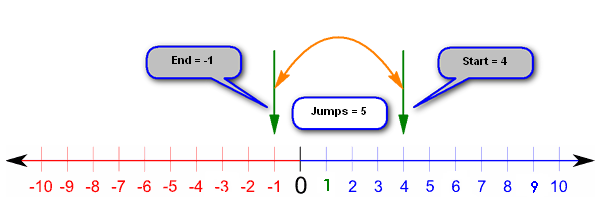
This time we are taking away a positive number from a number which is in fact smaller, so the result will be negative in this particular case. We start at 4, and following the rule “subtracting a positive moves us to the left” we jump to the left 5 times arriving at an end result of -1, and in fact this is our answer:
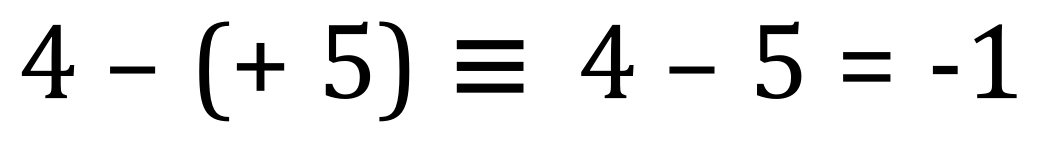
Study these examples and just like before hopefully this will become clear:
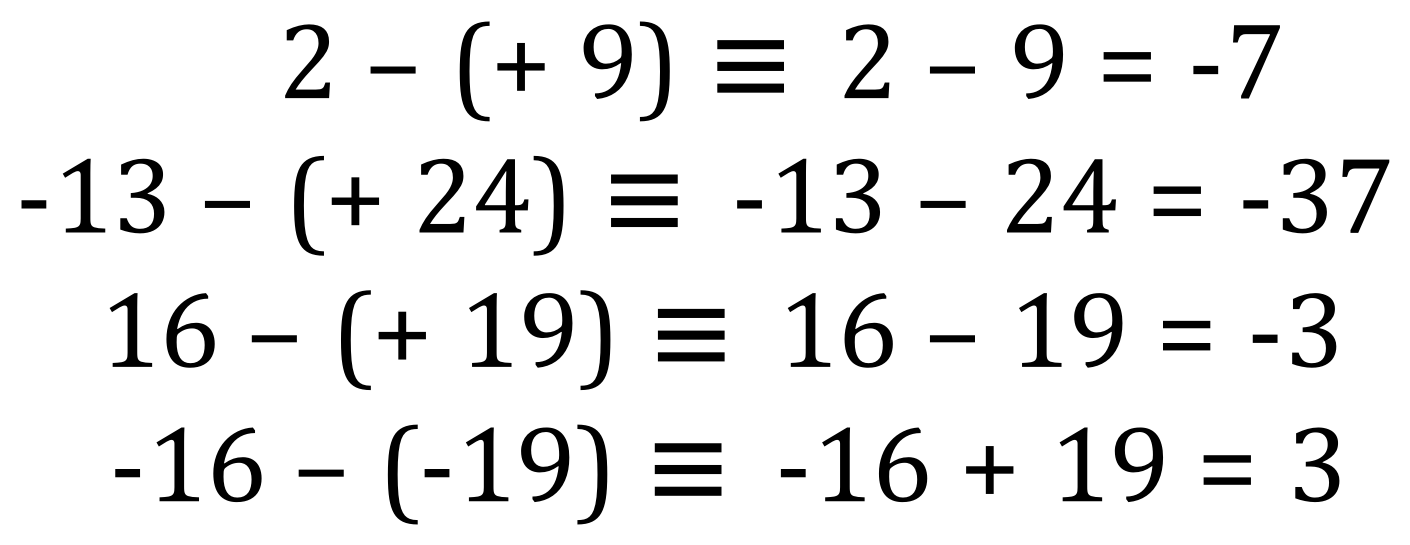
Goto >> Questions <<