Multiplication
When we were at school, one of the first things we learnt was the “Times Tables”, from 2×2 right up to 12×12, but in some cases up to 20×20 and we were meant to memorise these so that if we were asked for example what 8×4 was we could immediately respond 32. In this particular section I will deal with multiplication and division separately, starting with multiplication, looking at an old system that will probably a little bit familiar with called “long multiplication”
Before I do any of that, I have reproduced below a grid of the “Times Tables” up to 20×20 simply for ease of reference:
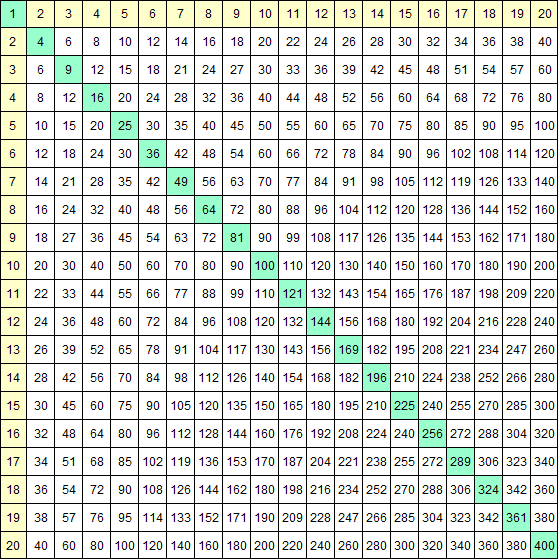
The way to use the table is to select the number from the top row in yellow that you wish to multiply by the number in the left-hand column in yellow, where the row and column intersect, there is your answer. Just out of interest you will see that some columns have intersection points shaded in green because these are the first 20 squares.
You can of course if you wish, simply use this table when you need to multiply numbers up to 20×20 but you will need a grasp of “long multiplication” if you wish to multiply larger numbers.
Multiplication
Let’s take a look at an example of multiplying 2 numbers together which are not on this grid.
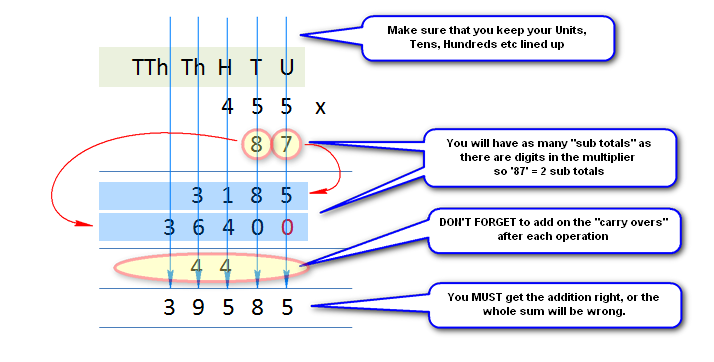
Well, this one looks particularly beastly and as you can see I have retained the hundreds tens and units column headers but this time I have added thousands and tens of thousands (

Th and TTh) because when we start looking multiplication we are really starting to hit some big numbers. Now there are two ways of starting this calculation and it would appear that the more modern way is to multiply the units first followed by the tens and if necessary followed by the hundreds and thousands and so on.
The only difference of course is that the sub totals will appear in the answer box in a different order other than that the process is pretty much the same. Okay, starting with the units column we need to evaluate 5×7.
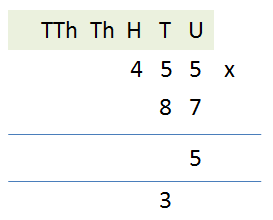
Using our table we can see that 5 times 7 is 35 which of course is 3 tens and 5 units, so we put the 5 in the answer box underneath the 7 in the units column and, just like in addition we “carry” the 3 across to the tens column:
Our interim answer is now starting to look like this.
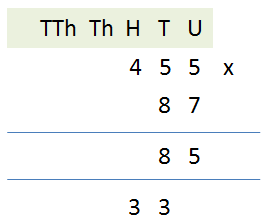
We stick with the 7 on the bottom line, but this time we multiply by the 5 on the top line under the tens, coincidently the answer again is 35 but remember that we carried 3 from the previous operation on the units, so we must add this to the 35 to make 38. We put the 8 to the left of the 5 in the answer box so it sits in the tens column and we carry the 3.
Our final step in this particular part of the calculation is to now multiply the 7 by the 4 making 28. Not forgetting the 3 we carried from the previous operation 28 becomes 31, we put
the one in the hundreds column underneath the 4 in the answer box and because we have no further operations to perform on the 455 line we put the 3 next to it underneath the thousands column as its first entry.
What we’ve actually got here is the first part of the answer which is 455×7 = 3185
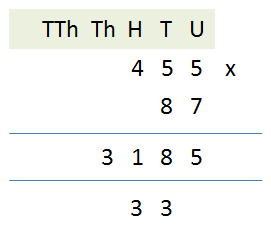
What we need to do now is work out the second part which is 455×80 and then add the two sub totals together to make the final sum.
Because the steps are almost identical in this second part, I am not going to go through them all except for the first step which is a little bit different.
Because we have completed our operations involving the units on the bottom line (that is on the 7 in 87) what we now need to do is to multiply the 8 (of the 87) by each element in 455 and on the second row, below where it says 3185 write out the subtitle of this particular second step:

The red 0 beneath the 5 in the units column the answer box is a placeholder, telling us that first of all we have finished with the units and that secondly our answers in the second step must be displaced one place to the left because we are now dealing with numbers which are 10 times bigger.
Look at the diagram and you can see that the red 0 is in place and that 8×5 which is 40 has been calculated, the 0 has been placed under the 8 in the tens column of the answer box and the 4 (which represents hundreds) has been placed outside the answer box underneath the hundreds column ready to be added to the next step.
As I said above, I’m going to now complete the sum, so what you need to do is study the next picture carefully to see if you can work out where the steps came from.
455×87 = 39585
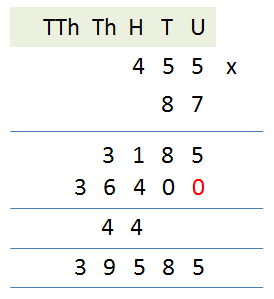
The 44 in the bottom but one box is just the “carry overs” from the intermediate steps in the calculation, the most important part is using your knowledge of addition to make sure that you correctly add up 3185 and 36,400 to get to the right answer, which of course in this case as above is 39,585.
The next picture is the same some, but “annotated” with some useful information for you to bear in mind when you’re doing sums of this type.