Balancing Chemical Equations
Balancing chemical reactions can be a daunting prospect for a lot of students.
The key to remembering this, is to remember the "law of conservation of matter" which tells us that "matter cannot be created nor destroyed". What this means is that if you have a certain total number of atoms before the reaction, you must have exactly the same number of atoms after the reaction i.e. in the products.
The number of molecules might change, for example you could start off with four molecules as reactants which become two molecules of product, but the number of atoms taking part in the whole thing will never change.
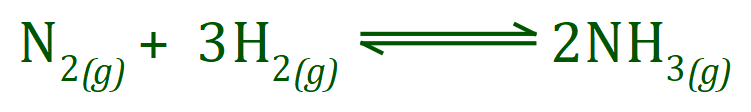
Let us take for example the reaction between Hydrogen and Nitrogen in the Haber process. We start off with four molecules in total on the left-hand side (one molecule of Nitrogen and three molecules of Hydrogen), but we end up with only two molecules of Ammonia. We have not, however, lost anything because if we add up the numbers of atoms in those molecules we will find that the number of atoms we started with is indeed the number of atoms that we finished with.
Look at the number of Nitrogen atoms on the left-hand side, Nitrogen in its normal state is a diatomic gas so this means that we have two atoms of Nitrogen in a single N2 molecule. from the equation above you can also see that we have three molecules of diatomic Hydrogen gas which is six atoms in total (two atoms in each H2 molecule, three H2 molecules in total). If we start off with two Nitrogen and six Hydrogen we have to finish with two Nitrogen and six Hydrogen otherwise we have contravened the law of conservation of mass!
Take a look at the Ammonia molecule, the Ammonia molecule contains one atom of Nitrogen and three atoms of Hydrogen. The equation showing the process of creation of Ammonia shows is that we do in fact end up with two molecules of Ammonia, which I'm sure you can see will contain two atoms of Nitrogen and six atoms of Hydrogen, exactly what we started with. So we have not contravened the law of conservation of mass, everything is fine.
Of course, in this example I gave you the balanced reaction to prove the point, but I may well have just given you the word equation, or the symbolic representations of the elements involved. This would have made the matter slightly more complicated and would have involved you actually making the balance work. This is the whole idea of this particular section.

This time, things are not quite so straightforward. I have shown you that we use Nitrogen and Hydrogen and correctly shown these gases in their diatomic state, I have also shown you that the product is Ammonia, but in this unbalanced form you should be able to see straight away that there is something wrong, for example we appear to have "lost" one of the Nitrogen atoms and we appear to have gained a Hydrogen atom!
This of course cannot be right (also this is a special case as the Haber process reaction is in fact a two-way, or reversible, reaction but it doesn't affect the balance, it is shown here as one way simply for a convenience).
This leads us to the reason for this particular topic, how to make sure that the equations are properly balanced. Perhaps the best way to do this is to count and make a table if you like of all of the atoms of the different elements on the reactant side (the left hand side) of the equation and make sure that we have the same numbers of the same elements on the product side (the right-hand side) of the equation.
Example 1 - Let's take a look at a fairly straightforward example involving the reaction between Potassium metal and water:

You may have seen this reaction performed in the laboratory at school, a small piece of potassium is dropped into a trough of water thereupon it starts to skate around on the surface of the water, fizzing violently and it may even catch fire. What is happening is that the Potassium metal is reacting with the water to produce a solution of Potassium Hydroxide and release Hydrogen gas. It is in fact the Hydrogen gas that catches fire.
The letters appearing in the subscripts are what are known as "state symbols" of which there are four that you should learn:
(s) = this tells you that the substance is in the solid-state.
(l) = this tell you that the substance is in the liquid state.
(g) = this tells you that the substance is a gas.
(aq) = this tells you that the substance is in its aqueous state, in other words a solution in water.
It is important that you get used to using these state symbols.
Moving back to the reaction between Potassium and water, we can see that we have one Potassium atom on each side of the equation, similarly we have one Oxygen atom on each side of the equation but when we get to Hydrogen, there is already a problem because we have three Hydrogen atoms on the right-hand side but we only started off with two!
We need to add more Hydrogen to the left-hand side, so let's start by doubling the amount of water that we use:

While this does seem to have fixed to a certain extent the Hydrogen issue, because now we have four on the left-hand side, but we still only have three on the right and side so we have in fact got nowhere. Let's take a look at doubling the amount of Potassium Hydroxide that we are producing on the right-hand side:

How many Hydrogen do we now have on the left-hand side? Well the answer is four. How many Hydrogen do we now have on the right and side?, four! . Well it appears we've done it, except for the fact that we haven't taken into account that we now appear to have gained a Potassium atom on the right-hand side. we certainly have the correct number of Hydrogen on each side (four) and we have the correct number of Oxygen on each side (two), but somehow we need to fix that extra Potassium atom, and the simple way to do this is to double up the amount of Potassium that we start with from one atom to two:

As a final check, count the number of the different atoms that you have on the left and the right hand side to make sure that your balance is in fact correct:
Potassium on the left = 2, Potassium is on the right = 2
Hydrogen on the left = 4, Hydrogen on the right = 4
Oxygen on the left = 2, Oxygen on the right = 2
It looks like we've done it! Indeed the last equation containing two Potassium atoms is the correct balanced equation for this reaction complete with the correct state symbols.
Example 2 - let's take a look at the equation between Aluminium and Oxygen which produces Aluminium Oxide (Alumina):
The basic (unbalanced) symbolic equation is this:

Just looking at this equation tells you that we start off with one Aluminium atom, and two Oxygen atoms (in one Oxygen molecule) and their products contains two Aluminium atoms and three Oxygen atoms, so clearly we have quite a bit of balancing to be done.
The most obvious thing to start off with is to double the Aluminium on the left so that we end up with two Aluminium on the right-hand side:

Well, that does appear to have sorted out the Aluminium problem, we still have too many Oxygen atoms in the product though. What about if we triple the amount of oxygen that we start with?

Oops, we have now got six Oxygen atoms on the left but only three on the right, hang on...... we can fix that by doubling the amount of aluminium oxide on the right-hand side:

Well we fixed the number of Oxygen because we got six on each side now (take a minute to show yourself that that's correct) but we still have a problem because we've got four Aluminium atoms on the right but we only started with two, what can we do about that?. I think you can probably see that we just need to double the number of Aluminium atoms that we started with:

This looks okay, let's check to make sure that it is:
Aluminium on the left = 4, Aluminium on the right = 4
Oxygen on the left = 6, Oxygen on the right = 6
Once again it appears we've succeeded. Just as an aside, you might sometimes see this reaction written this way:
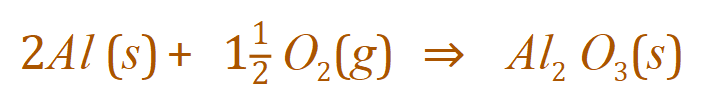
This is a perfectly acceptable alternative, although we wouldn't really have half a molecule of Oxygen it is quite permissible to write fractional amounts in your equations although the preferred format would be the one above (starting off with four Aluminium atoms).
Because this is such a tricky area, and seems to cause a lot of concern, let's take another look at how we might approach this problem. As you know by now we need to make sure that the numbers of the different types of atoms on the left is the same as the numbers on the right. You could utilise a grid, and the next three examples will show you one way to do this:
Example 3:
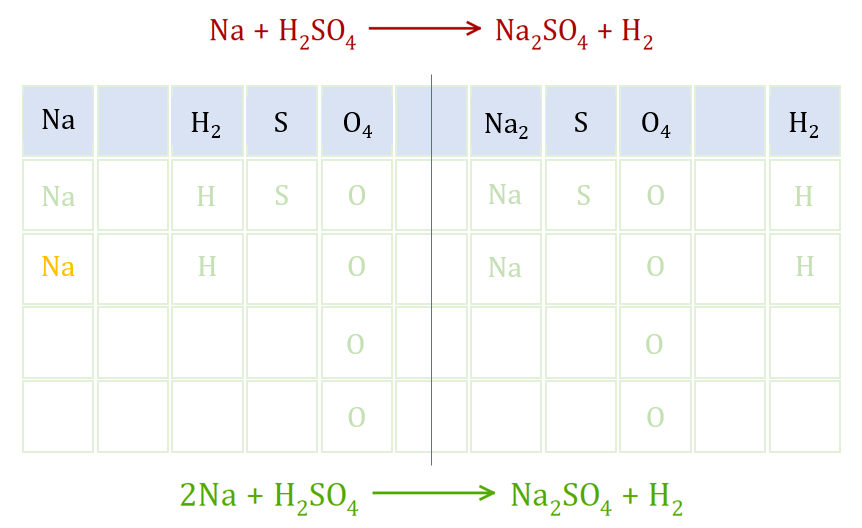
This is the equation of the reaction between Sodium metal and Sulphuric Acid. The equation in red at the top is the unbalanced version which simply shows us that the products of the reaction are Sodium Sulphate and Hydrogen gas. just simply glancing at the equation should show you that we have an imbalance of Sodium atoms, one on the left but two on the right.
In this grid method, I've broken down the reactants and products into their constituent elements, showing the numbers of each atom. This is the line which is highlighted in light blue. To address the imbalance of Sodium I have added a second Sodium atom (in orange) underneath the first one. We now have two Sodium atoms on the left and two Sodium atoms on the right so as far as that element is concerned we are balanced. It is best to work from left to right, so the next element we will look at is Hydrogen and straight away we can see that everything is in order there, because we have two on the left and two on the right. Moving on to Sulphur, you should also be able to see that we have a balance they already because we have one on the left and one on the right (in both cases forming part of the sulphate ion). Finally the element Oxygen, and again you should be able to see that straight away we have a balance, because the sulphate ion has not altered in the reaction and has remained intact with four Oxygen atoms.
Effectively then the only thing we've had to do to this equation is add one more Sodium atom to make the whole thing balance, and this is represented at the bottom of the graphic by the green equation which represents the balanced version.
Example 4:
This example shows us the reaction between Potassium Iodide and Lead Nitrate, usually both in aqueous solution in this experiment. This is a particular favourite of mine because the colour of Lead Iodide is perhaps the most beautiful yellow you will ever see, and the production of it is instantaneous.
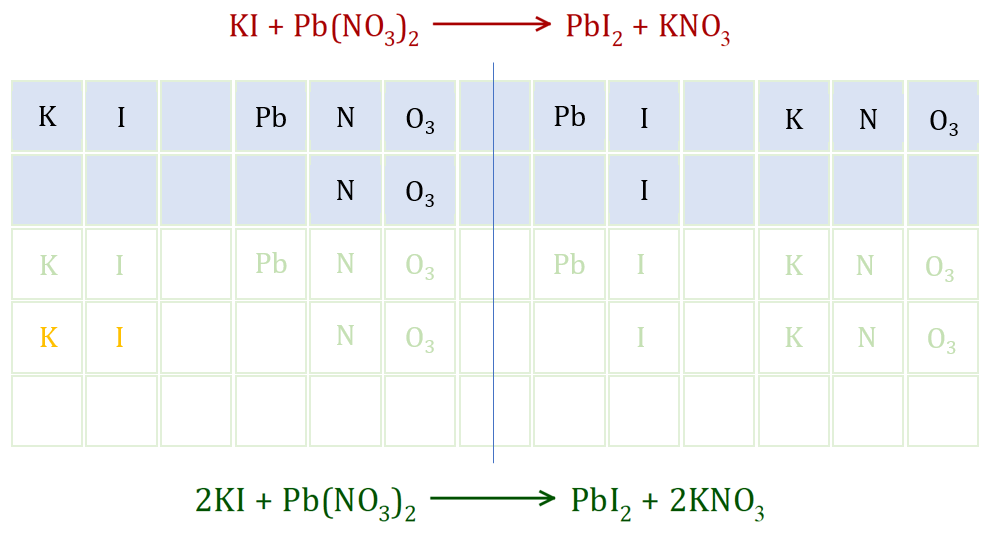
Step 1 - from the red (unbalanced) equation you can see that we are deficient of one Iodine atom and a complete Nitrate group, that is one Nitrogen and three Oxygen atoms extra are needed.
Step 2 - to produce the extra Iodine atom that we need, we double up the Potassium Iodide, which gives us one extra Potassium and one extra Iodine (both shown in orange).
Step 3 - the problem we face now is the fact that since we have doubled up the Potassium Iodide we have an extra Potassium atom and we still need one extra Nitrate group. We can account for this by doubling the amount of Potassium Nitrate that we have produced on the right-hand side.
Step 4 - looking at the equation now, it appears that we may have completed the problem but what we should do is count the atoms to make sure.
Potassium on the left = 2, Potassium on the right = 2
Iodine on the left = 2, Iodine on the right = 2
Lead on the left = 1, Lead on the right = 1
Nitrogen on the left = 2, Nitrogen on the right = 2
Oxygen on the left = 6, Oxygen on the right = 6
Everything seems to be in order, and our green equation is the correctly balanced version.
Example 5:
Example 3 is slightly different because it comes from the world of organic chemistry. This reaction is the combustion of Butane gas in oxygen to produce water and carbon dioxide. When you come to organic chemistry you'll see that if a hydrocarbon such as Butane burns cleanly (inorganic chemistry this is referred to as "completely" or "complete combustion" ), Water and Carbon Dioxide are the only products that will be made.
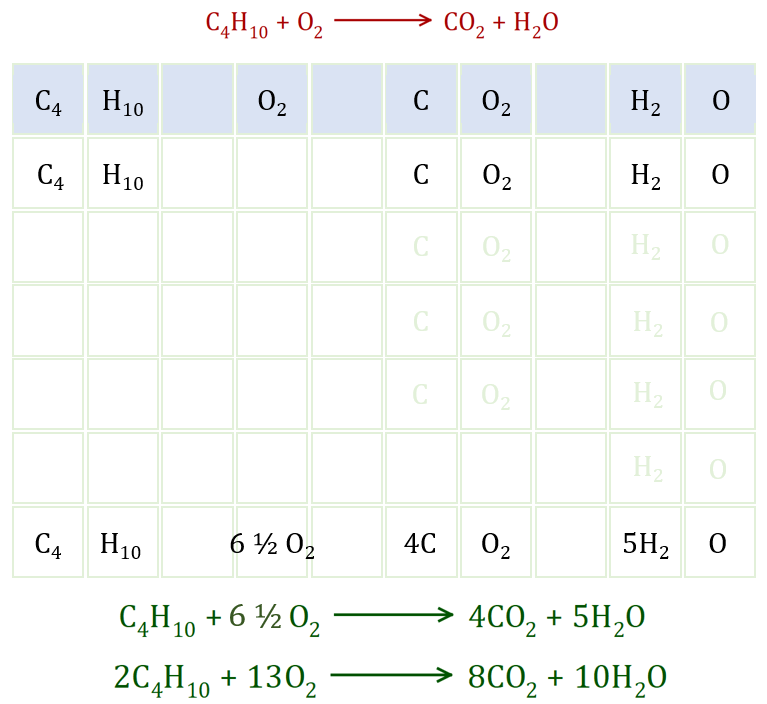
Looking at the unbalanced equation (in red), this simply states what I just already said, that the only products of this reaction are Carbon Dioxide and Water. By now you should be automatically going to the products and reactants and looking for the differences. You should be able to see that there are four Carbon atoms in one molecule of Butane so we would expect to produce four molecules of Carbon Dioxide. By a similar deduction you should be able to see that as Butane contains 10 Hydrogen atoms in total we are going to be looking at the production of five molecules of Water.
Step 1 - you can now break down the products showing the four molecules of Carbon Dioxide and five molecules of Water, this can get quite laborious when the molecules are quite large you may wish to just keep it to the element symbol and suffix which shows the number of atoms of that element, ie: you can if you wish write 8 O's or keep it as 4O2 .
Step 2 - we started off using only one molecule of Oxygen (two atoms) but since we've produced four molecules of Carbon Dioxide and five molecules of water, the Oxygen requirement has gone up from 2 to 13 atoms. we need an extra 11 Oxygen atoms and we can add these by adding another five and half molecules of Oxygen to the one that we already have.
Step 3 - adding our extra Oxygen, as discussed in step two we can now write out the balanced equation (the first of the two green equations) showing the fractional amount of Oxygen. This is a perfectly acceptable way to show the equation and in fact is the correct answer, however you may be asked not to use fractions in which case all you have to do is simply double everything up as shown in the second green equation.
Carbon on the left = 4, Carbon on the right = 4
Hydrogen on the left = 10, Hydrogen on the right = 10
Oxygen on the left = 13, Oxygen on the right = 13
Everything seems to be in order, and our first green equation is the correctly balanced version (but remember what I said about getting rid of the fraction if you need to).
Now click >> here << to attempt some more.