Base Multiplication
The golden rule with regard to multiplication is to remember the following 3 points and apply them constantly throughout the multiplication:
- If you’re working in base N remember this throughout
- Each step in the multiplication will be carried out in base 10
- The answer you come up with at every sub stage must be converted back to base N
This might sound very complicated but if you consider a couple of simple examples it will start to become very clear.
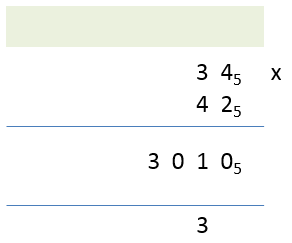
Example 1 - multiplication of the 2 numbers “34” and “42” both of which are base 5 numbers.

Step 1 - remembering point one above, you must constantly think “base 5” all through this. This multiplication is carried out in just the same way that you would if it was base 10, we drop a 0 under the unit’s column and proceed to multiply “4×4”
Step 2 - bullet point to comes into play here, this multiplication is carried out in base 10 but the result will be mentally converted to base 5, ergo “4×4 equal 16” which is “31” in base 5 so we place a 1 to the left of the 0 and we carry the 3:
Our calculation we now look like this:

Step 3 - we now multiply “4×3” to make 12, and on the 3 that we carried making 15 and convert 15 into its base 5 equivalent of “30”. We enter this in its entirety in the answer box which makes the first part of the answer 3010 in base 5:
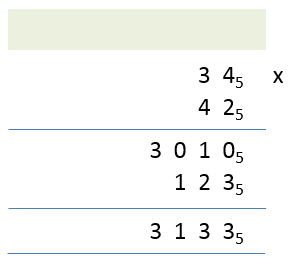
Step 4 - we now look at the second-half of the calculation and we start this by multiplying “2×4” which is of course 8 in base 10, “13” in base 5. We place a 3 under the rightmost 0 in the answer box and we carry the 1.
Step 5 - we now say “2×3” which makes 6 and we add the 1 that we carried making 7, but once again this is a base 10 number, its base 5 equivalent to being “12”. Since we have reached the end of the calculation replace the “one-two” in its entirety to the left of the 3 in the second part of the answer and we add the 2 together to get the final answer:
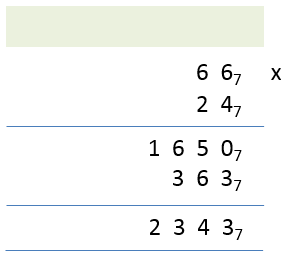
Example 2 - consider the base 7 numbers “66” and “24”, let’s multiply them together:

As before, remember the 3 rules, “think base 7”, “do the multiplications in base 10”, “convert back to base 7 before using the result”, okay?
Step 1 – Drop a 0 underneath the 47 and start the multiplication of “2 x 6” which is 12 in base 10, converting this to base 7 gives the equivalent “15”. Place the 5 to the left of the 0 and carry the 1.
Step 2 – Again (coincidentally) we have to evaluate “2 x 6” which again comes to “12”, we add to this the 1 that we carried previously making “13” which we convert to its base 7 equivalent of “16” and because this is the end of the first part we add it in its entirety to the answer box making the 1st part of the answer “1650”.

Step 3 - we continue now with the second-half of the calculation and we say to ourselves “4 x 6” equals 24 but once again remember that this is a base 10 number, we converted to space 7 equivalent which is “33”, we enter 3 below 7 in the answer box and carry the other 3.
Step 4 - the final step “4 x 6” equals 24 once again, we add to this the 3 we carried making 27 and we convert this to its base 7 equivalent of “36” which because we have now almost finished our calculation, we append in its entirety to the second part of the answer box. The second row the answer is now “3637” which we add to the “16507” to get our final answer as shown below: